1.Числовая последовательности и ее предел.

 Функция f(x) называется функцией целочисленного аргумента, если множество значений x, для которых она определена, является множеством всех натуральных чисел1, 2, 3,… Примером функции целочисленного аргумента может служить сумма n первых чисел натурального ряда. В данном случае

Числовой последовательностью называется бесконечное множество чисел

    (1)

следующих одно за другим в определенном порядке и построенных по определенному закону, с помощью которого   задается как функция целочисленного аргумента,   т.е.   .

Число А называется пределом последовательности (1), если для любого    существует число   , такое, что при   выполняется неравенство   . Если число А есть предел последовательности (1), то пишут

Числовая последовательность не может иметь более одного предела. Последовательность, имеющая предел, называется сходящейся.

Для сходящихся последовательностей имеют место теоремы:

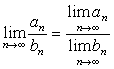
 если   .

2. Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.

Определение предела по Коши. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для каждого ε > 0 существует δ > 0 такое, что для всех x, удовлетворяющих условию |x – a| < δ, x ≠ a, выполняется неравенство |f (x) – A| < ε.

Определение предела по Гейне. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для любой последовательности   такой, что   сходящейся к числу a, соответствующая последовательность значений функции  сходится к числу A.

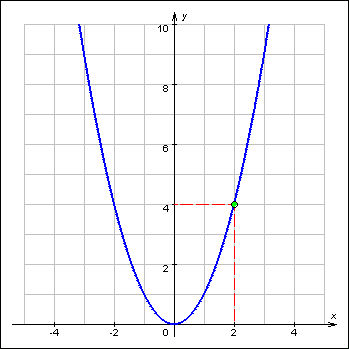
График 1.3.6.1. Предел функции y = x2 при x → 2.

График 1.3.6.2. Предел функции   при x → 0.

Если A – предел функции в точке a, то пишут, что 

Определения предела функции по Коши и по Гейне эквивалентны.

3. Пределы с неопределенностью вида   и метод их решения

Сейчас мы рассмотрим группу пределов, когда  , а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены

Пример:

Вычислить предел 

Согласно нашему правилу попытаемся подставить бесконечность в функцию. Что у нас получается вверху? Бесконечность. А что получается внизу? Тоже бесконечность. Таким образом, у нас есть так называемая неопределенность вида  . Можно было бы подумать, что  , и ответ готов, но в общем случае это вовсе не так, и нужно применить некоторый прием решения, который мы сейчас и рассмотрим.

Как решать пределы данного типа?

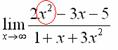Сначала мы смотрим на числитель и находим   в старшей степени: Старшая степень в числителе равна двум.

Теперь смотрим на знаменатель и тоже находим   в старшей степени: 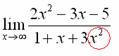Старшая степень знаменателя равна двум.

Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.

Итак, метод решения следующий: для того, чтобы раскрыть неопределенность   необходимо разделить числитель и знаменатель на   в старшей степени.

Разделим числитель и знаменатель на 

Вот оно как, ответ  , а вовсе не бесконечность.

4. Пределы с неопределенностью вида   и метод их решения

в числителе и знаменателе находятся многочлены, но «икс» стремится уже не к бесконечности, а к конечному числу.

должно выглядеть примерно так:

Разложим числитель на множители.