4.3.2 Уравнение движения жидкости в трубопроводе

Для составления уравнения движения дизельного топлива в трубопроводе низкого давления воспользуемся вторым законом Ньютона.

Предположим, что скорость движения жидкости изменяется только в направлении оси ОХ, тогда второй закон Ньютона примет вид

.

(4.51)

Выделим в потоке вязкой жидкости элементарный объем с размерами ребер dx, dy, dz (рис. 4.4). На выделенный объем действуют три вида сил: сила тяжести, равнодействующая сил давления отброшенной части жидкости и равнодействующая сил трения.

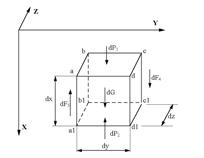
Рис. 4.4 Схема сил, действующих на элементарный объем в потоке жидкости

Найдем проекции этих сил на ось ОХ. Сила тяжести приложена в центре масс выделенного объема и ее проекция на ось ОХ равна

dG=rqdV. (4.52)

Равнодействующая сил давления определяется из следующих соображений: если на грани abcd (рис. 4.4) давление жидкости равно r, то сила Р действующая на площадку dydz составит

dP₁=pdydz. (4.53)

На нижней грани a₁b₁c₁d₁ с точностью до второго члена разложения в ряд Тейлора давление составит p₁=p+(dp/dx)dx, и на эту грань действует сила противоположно направленная скорости движения жидкости

dP₂=-(p+dp/dx)dydz. (4.54)

Равнодействующая сил давления равна их алгебраической сумме

.

(4.55)

Так как скорость изменяется только в направлении оси Х, то силы трения возникнут на боковых гранях aba₁b₁ и dcd₁c₁ выделенного объема. При этом

, и ,

(4.56)

где J — скорость движения топлива вдоль оси ОХ.

Равнодействующая сил трения, отнесенного к единице объем

,

(4.57)

где m — динамическая вязкость топлива;

dV=dxdydz — элементарный объем.

Суммируя силы dG, dP и dF получим проекцию равнодействующей силы на ось О

.

(4.58)

Учитывая, что масса выделенного объема m=rdV, и, подставляя (4.58) в (4.51), после преобразований получим уравнение движения жидкости вдоль оси ОХ

.

(4.59)

Все слагаемые уравнения (4.59) имеют размерность силы, отнесенной к единице объема. На основании понятия о полном дифференциале имеем

.

(4.60)

В выражении (4.60) производная характеризует изменение скорости по времени в какой-либо точке жидкости; остальные слагаемые правой части уравнения характеризуют изменение скорости при переходе от точки к точке.

При установившемся движении топлива в трубопроводе ускорение равно нолю, т.е.

a=dJ/dt=0. (4.61)

Подставляя (4.60) в (4.50) после приведения подобных и преобразований, получим

.

(4.62)

Если трубопровод расположен горизонтально и ось ОХ совпадает с осью трубопровода, то проекция силы тяжести на ось равна нолю. Тогда уравнение (4.62) примет вид

.

(4.63)

Левая часть уравнения (4.63) не зависит от координаты х, так как скорость может изменяться только вдоль осей OY и OZ, а вдоль оси OX J=const.

Правая часть уравнения (4.64) зависит от координаты х, поэтому обе части данного уравнения могут быть равны только постоянной величине, т.е.

,

(4.64)

где l — длина трубопровода.

С учетом (4.63) уравнение движения примет вид:

.

(4.65)

Уравнение (4.65) является незамкнутым, так как помимо скорости J в него входит еще неизвестная давления р, поэтому необходимо составить еще одно уравнение, связывающее параметры J и р. Таким уравнением является уравнение неразрывности потока жидкости.