5.1. Кореляційний аналіз та прогнозна математична модель взаємозв’язку концентрації нікелю у воді та водневого показника середовища
Щоб визначити залежність між досліджуваними об’єктами ми звернулися до кореляційного аналізу і методу парної кореляції за допомогою коефіцієнта Пірсона, який виглядає так:
В нашому випадку xi – концентрація важкого металу: Ni, Co, Pb, Zn, Cd, Fe, Cu, Mn, yi − показник pH води.
Дані розрахунки проводилися за таким зразком:
0,0112
= 7,6
= 0,5
Значення коефіцієнта Пірсона для досліджуваних нами металів вносимо у таблицю (табл. 5.1.1).
Таблиця 5.1.1
Кореляційна залежність між концентрацією важких металів та водневим показником води
Місяць |
Ni |
Co |
Pb |
Zn |
Cd |
Fe |
Cu |
Mn |
Вересень |
0.5 |
0.9 |
0 |
0.3 |
0 |
0.7 |
0.9 |
0 |
Жовтень |
0.9 |
0.7 |
0 |
0.2 |
0 |
0.4 |
0.3 |
0.3 |
Листопад |
0.9 |
0.5 |
0,1 |
0.6 |
0 |
0.6 |
0.6 |
0.4 |
Грудень |
0.2 |
0.8 |
0 |
0.7 |
0 |
0.2 |
0.6 |
0.2 |
Січень |
0.4 |
0.9 |
0 |
0.4 |
0 |
0.3 |
0.3 |
0.4 |
Лютий |
0.9 |
0.8 |
0 |
0.1 |
0 |
0.4 |
0.1 |
0.8 |
Середнє |
0.9 |
0.7 |
0,1 |
0.4 |
0 |
0.5 |
0.6 |
0.3 |
Виявлення ключових факторів.
Кореляційний аналіз свідчить сильний взаємозв’язок між концентрацією нікелю і водневим показником води (коефіцієнт кореляції – в середньому 0,9). А такі метали, як свинець і кадмій виявляють найслабший взаємозв’язок з водневим показником (коефіцієнт кореляції – 0,1). Тому для дослідження ми вибрали нікель.
Для того щоб створити прогнозну математичну модель, перш за все необхідно побудувати графік кореляційної залежності. Спершу нам потрібно звести досліджувані дані в таблицю (табл.5.1.2).
Таблиця 5.1.2
Залежність концентрації нікелю від водневого показника
|
Вересень |
Жовтень |
Листопад |
Грудень |
Січень |
Лютий |
X(Концентрація Ni) |
0,0112 |
0,0041 |
0,0038 |
0,019 |
0,009 |
0,025 |
Y(pH) |
7 ,6 |
7,4 |
6,9 |
5,9 |
6,5 |
6,4 |
Використовуючи дані наведені в таблиці (табл.5.1.2) будуємо графік кореляційної залежності концентрації нікелю від водневого показника середовища (рис.5.1.3). Відклавши точки на кореляційному полі в нас виходить лінійна регресія.
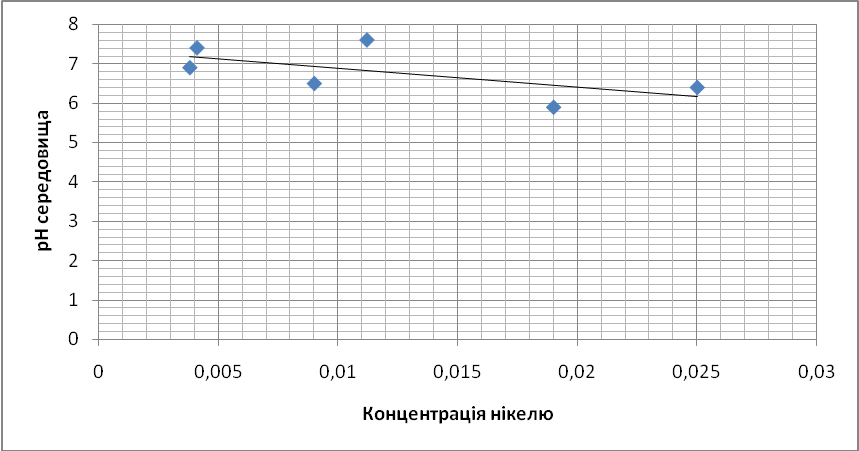
Рис.5.1.3. Кореляційне поле досліджуваних явищ
Далі, щоб отримати прогнозну модель ми використовуємо метод найменших квадратів. Дане рівняння виглядає так:
Потім із досліджуваних явищ складаємо таблицю (табл. 5.1.4), яка необхідна для розв’язання рівняння регресії.
Таблиця 5.1.4
Статистична таблиця дослідження
X |
Y |
Xy |
X2 |
0,034 |
7,9 |
0,2686 |
0,001156 |
0,0273 |
8,3 |
0,22659 |
0,0007452 |
0,0396 |
8,9 |
0,35244 |
0,0015681 |
0,03 |
7,9 |
0,237 |
0,0009 |
0,0466 |
8,4 |
0,39144 |
0,0021715 |
0,0266 |
7,4 |
0,19684 |
0,0007075 |
0,2041 |
48,8 |
1,67291 |
0,0072483 |
Виходячи з розв’язаного рівняння, прогнозна математична модель залежності концентрації заліза від водневого показника води виглядає таким чином:
Так, як водневий показник середовища є одним із визначальних чинників зміни концентрації нікелю у воді, то його коливання призводять до коливань концентрації металу у воді. Після проведеного дослідження ми бачимо що ця залежність є прямо пропорційна. Використання даної прогнозної моделі дає нам можливість визначати приблизну концентрацію досліджуваного металу в залежності від зміни водневого показника без додаткових досліджень.
Проаналізувавши модель залежності концентрації нікелю від водневого показника (коефіцієнт детермінації 0,52) ми переконалися в тому, що наша модель є достовірною, адже, коли КД становить більше 50%, то модель побудована вірно.