3.Бескоалиционные игры

Рассмотрим бескоалиционную игру, когда каждый игрок действует самостоятельно. Пусть — множество игроков. Каждый из игроков имеет некоторое множество своих стратегий. Число стратегий образует множество стратегий каждого игрока, и это число должно быть не меньше двух.

Процесс игры состоит в выборе каждым игроком своей стратегии . В результате этого выбора определяется исход партии: 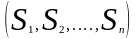. Пусть — вектор ситуаций в игре, тогда — множество всех ситуаций в игре. С другой стороны, множество всевозможных ситуаций S можно рассматривать как . Выигрыш каждого игрока в каждой ситуации определяется следующим выражением:

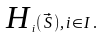
Тогда после всех введенных обозначений бескоалиционной игрой называют систему следующего вида:

В бескоалиционной игре все множества являются множествами вещественных чисел. Среди явлений, описываемых посредством бескоалиционных игр, довольно много таких, когда по результатам игры приходится распределять некоторые ресурсы.

В теории игр также выделяют игры с постоянной суммой: бескоалиционная игра называется игрой с постоянной суммой, если существует такая константа c, что выполнятся условие Если 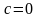, то бескоалиционная игра называется игрой с нулевой суммой.

4.Приемлемые ситуации и ситуации равновесия в игре

Опр.: Ситуация 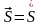называется приемлемой для i-ого игрока, если он, изменяя свою ситуацию на ситуацию 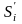, не может добиться увеличения своего выигрыша.

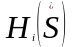— выигрыш i-ого игрока

Последнее условие характеризует ситуацию, приемлемую для i-ого игрока.

Опр.: Ситуация S, приемлемая для всех игроков, называется ситуацией равновесия в игре.

Исходя из принятой методики оценки предпочтения ситуаций видно, что в ситуациях равновесия и только в них ни один из игроков объективно не заинтересован в отклонении от ситуации равновесия за счет изменения своих стратегий.

Если ситуация равновесия достигнута в результате переговоров, то ни один из участников не заинтересован в нарушении этого договора.

Стратегия игрока, входящая хотя бы в одну из ситуаций равновесия, называется равновесной.

Основная часть теории бескоалиционных игр состоит в разработке методов нахождения ситуаций равновесия и исследования их свойств. Процедуру нахождения ситуации равновесия называют решением бескоалиционной игры.

5.Стратегическая эквивалентность игр

Разнообразие бескоалиционных игр требует их объединения в классы эквивалентности. Каждый из классов можно исследовать на примере игры с простой структурой. Стратегическая эквивалентность является обоснованием для объединения игр в один класс, а это означает, что игры, объединенные в один класс, считаются стратегически эквивалентными.

Опр.: Пусть имеется две игры 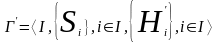и . Тогда эти игры называются стратегически эквивалентными, если , при котором выполняется следующее условие:

Обычно условие стратегической эквивалентности записывают следующим образом: .

Стратегическая эквивалентность обладает следующими свойствами:

1. рефлексивность ;

2. симметрия и ;

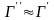Док-во:

,

Стратегическая эквивалентность позволяет разбить все множество бескоалиционных игр на попарно непересекающиеся классы:

Различия в стратегически эквивалентных играх заключаются в масштабах выигрыша и в начальном капитале . Стратегия в каждой из этих игр заключается в максимизации своего выигрыша, причем этот выигрыш максимизируется на одинаковых стратегиях.

Теорема: стратегически эквивалентные игры имеют одни и те же ситуации равновесия.

Доказательство:

Пусть имеется две стратегически эквивалентные игры: . Это значит, что в ситуации равновесия должно выполняться условие:

,

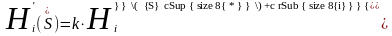Очевидно, меняя ситуацию равновесия на другую ситуацию равновесия , получим:

.

Так как 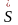— ситуация равновесия, то для игры должно выполнятся условие:

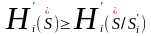, но из этого неравенства следует, что 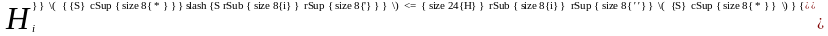, а это условие означает, что ситуация есть ситуация равновесия для двух игр и , то есть две стратегически эквивалентные игры имеют одну и туже ситуацию равновесия . Теорема доказана.

Теорема: всякая бескоалиционная игра с постоянной суммой стратегически эквивалентна некоторой бескоалиционной игре с нулевой суммой.

Доказательство:

Рассмотрим бескоалиционную игру с постоянной суммой:

, , .

Возьмем такие произвольные вещественные числа , 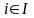, чтобы . Рассмотрим функцию выигрыша 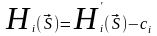. Это есть условие стратегической эквивалентности игр и (т.к. k=1, а не зависит от S). Тогда выигрыш игры Г равен . То есть игра Г является игрой с нулевой суммой. Теорема доказана.

Таким образом, мы доказали, что игры с постоянной суммой всегда можно привести к играм с нулевой суммой.