Билет №16

1. Внутренняя энергия идеального газа.

В теории идеального газа потенциальная энергия взаимодействия молекул считается равной нулю. Поэтому внутренняя энергия идеального газа определяется кинетической энергией движения всех его молекул. Средняя энергия движения одной молекулы равна

Так как в одном киломоле содержится   молекул, то внутренняя энергия одного киломоля газа будет

Учитывая, что   , получим

Для любой массы m газа, т.е. для любого числа киломолей   внутренняя энергия

Из этого выражения следует, что внутренняя энергия является однозначной функцией состояния и, следовательно, при совершении системой любого процесса, в результате которого система возвращается в исходное состояние, полное изменение внутренней энергии равно нулю. Математически это записывается в виде тождества

2. Закон Ома в дифференциальной форме.

Закон Ома в интегральной форме для однородного участка цепи (не содержащего ЭДС)

Для однородного линейного проводника выразим R через ρ:

ρ – удельное объемное сопротивление; [ρ] = [Ом·м].

      Найдем связь между   и   в бесконечно малом объеме проводника – закон Ома в дифференциальной форме.

      В изотропном проводнике (в данном случае с постоянным сопротивлением) носители зарядов движутся в направлении действия силы, т.е. вектор плотности тока   и вектор напряженности поля   коллинеарны (рис. 7.6).

Рис. 7.6

      

Исходя из закона Ома, имеем:

      А мы знаем, что   или  . Отсюда можно записать

      это запись закона Ома в дифференциальной форме.

Здесь   – удельная электропроводность.

Размерность σ – [ ].

      Плотность тока можно выразить через заряд электрона е, количество зарядов n и дрейфовую скорость  :

.

      Обозначим  , тогда  ;

Теперь, если удельную электропроводность σ выразить через е, n и b:   то вновь получим выражение закона Ома в дифференциальной форме:

.

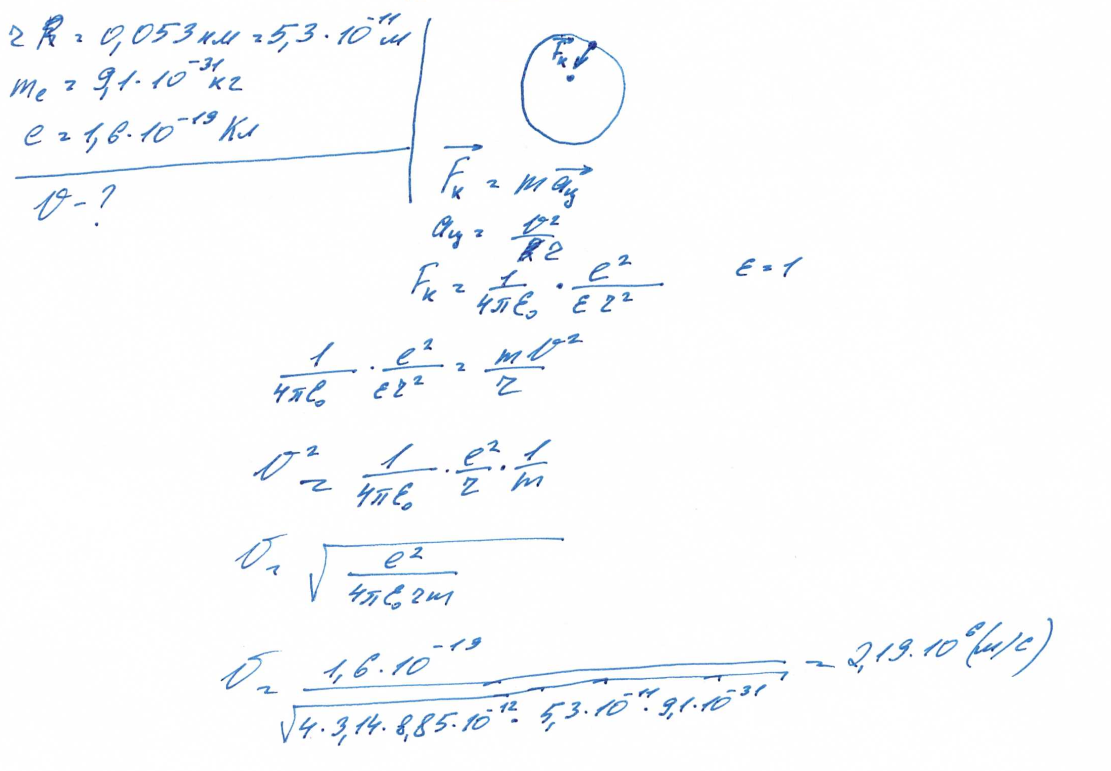
3. В элементарной теории атома водорода принимают, что электрон обращается вокруг ядра по круговой орбите. Определить скорость электрона, если радиус вращения r = 0,053 нм. (m_e = 9,1  10^-31кг, е = 1,6  10^-19Кл).

Билет №17

1. Адиабатический процесс. Цикл Карно.

Адиабатический процесс - это процесс, при котором отсутствует теплообмен с окружающей средой, следовательно, dQ = 0. К адиабатическим процессам можно отнести все быстро протекающие процессы. Например, процесс распространения звука в среде. Скорость распространения звука настолько велика, что процесс обмена энергией между звуковой волной и средой произойти не успевает и т.д. и т.п.

Из I начала термодинамики получают, что dA = –dU, т.к. dQ = 0, т.е. внешняя работа совершается за счет изменения внутренней энергии системы. Для произвольной массы газа имеем:

Если продифференцировать уравнение Менделеева-Клапейрона, то получим

Исключив T, получим

Интегрирую обе части от P₁ до P₂ и от V₁ до V₂, получим

Т.к. состояния 1 и 2 выбраны произвольно, то можно записать, что

PV ^ = const.

Полученный результат есть уравнение адиабатического процесса, или уравнение Пуассона. Перейдя к переменным T и V или к переменным P и T, используя уравнение Менделеева-Клапейрона, получим

TV ^–1 = const; T ^P ^1– = const.

Эти формулы тоже выражают уравнение Пуассона, только в других параметрах.

Для одноатомных газов i = 3,  = 1,67; для двухатомных газов i = 5,  = 1,4.

Значение , вычисленное по формуле, хорошо подтверждается экспериментом.

Диаграмма адиабатического процесса изображается гиперболой.

Вычислим работу, совершаемую газом в адиабатическом процессе. Если газ адиабатически расширяется от V₁ до V₂, то его температура уменьшается от T₁ до T₂.

Произведя некоторые преобразования, можно перейти к виду

Работа, совершаемая газом при адиабатическом расширении, меньше, чем при изотермическом. Это можно объяснить тем, что при адиабатическом расширении происходит охлаждение газа, тогда как при изотермическом – температура поддерживается постоянно за счет притока извне эквивалентного количества теплоты.

Рассмотренные процессы имеют общую особенность – они проходят при постоянной теплоемкости; в первых двух процессах они соответственно равны C_V и C_P. При изотермическом процессе dt = 0, теплоемкость равна . В адиабатическом процессе dQ = 0, следовательно, теплоемкость тоже равна нулю.

Процесс, при котором теплоемкость остается постоянной, называется политропным.

Исходя из I начала термодинамики, при условии, что теплоемкость постоянна, выводится уравнение политропы:

Очевидно, что при C = 0 n = , получаем уравнение адиабаты. При C =  n = 1, получаем уравнение изотермы. При C = C_P n = 0, получаем уравнение изобары. При C = C_V n = , получаем уравнение изохоры. Таким образом, все процессы являются частным образом от изотропного процесса.

Анализируя работу тепловых двигателей, французский инженер С. Карно в 1824г. пришел к выводу, что наивыгоднейшим круговым процессом является обратимый круговой процесс, состоящий из двух изотермических и двух адиабатических процессов, т.к. он характеризуется наибольшим коэффициентом полезного действия. Такой цикл получил название цикла Карно. В прямом цикле Карно рабочее тело изотермически, а затем адиабатически расширяется, после чего снова изотермически (при более низкой температуре) и потом адиабатически сжимается. Т.е. цикл Карно ограничен двумя изотермами и двумя адиабатами.

При изотермическом расширении от нагревателя отбирается тепло   (на участке 1-2 рис. 9.11). Вследствие этого температура газа поддерживается неизменной. Соответственно, параметры точки 2 будут равны   . На участке 2-3 происходит адиабатное расширение. Внутренняя энергия газа уменьшается и его температура падает до Т₂. Параметры точки 3 -   . На участке 3-4 газ изотермически сжимается. Параметры точки 4 -   . Выделяющееся при этом тепло   отбирается холодильником. Участок 4-1 -адиабатическое сжатие до исходного состояния, соответствующего точке 1. Таким образом, завершен цикл “1-2-3-4-1 и в итоге нагреватель отдал газу теплоту   , а холодильник отобрал   Разность   определяет полезную работу газа за один цикл, так как согласно I началу термодинамики   , но для кругового процесса   и, следовательно   .

Отношение полезной работы к затраченной энергии нагревателя определяет коэффициент полезного действия (к.п.д.) тепловой машины:

Эта формула справедлива для любого обратимого и необратимого процесса.

Определим коэффициент полезного действия цикла Карно для обратимого процесса. Теплота подводится на участке 1-2 и отводится на участке 3-4. Для изотермического процесса внутренняя энергия Q=const и все подводимое тепло расходуется на работу  .

Тогда или Для изотермического процесса работа   С учетом последних выражений

Покажем, что

Так как процессы на участках 2-3 и 1-4 адиабатические, для определения связи между   и   и   и  используем уравнение Пуассона в виде 

Следовательно, и Разделим эти уравнения и получим Тогда выражение для к.п.д. (9.24) примет вид

Эта формула справедлива только для обратимого цикла Карно.

Теоремы Карно.

1 Все обратимые машины, работающие по циклу Карно, имеют, е зависимо от природы рабочего тела, одинаковый КПД при условии если у них общий нагреватель и холодильник.

2 Если две тепловые машины имеют общий нагреватель и холодильник и одна обратимая, а другая необратимая, то КПД обратимой больше необратимой