Домашнее задание №3. Тема: «Комбинаторика»

Задание. Решить комбинаторные задачи. Дать пояснения к решению. Без пояснения задача считается нерешенной.

1 Вариант

1. Найти коэффициент при 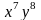в разложении бинома .

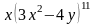2. В научном отделе работает 50 человек. Из них 27 человек знают английский язык, 15 − немецкий язык, 20 − итальянский язык, 6 – английский и немецкий, 8 – английский и итальянский, 3 – немецкий и итальянский; все три языка знают 2 человека. Определить: а) сколько человек не знают ни одного из этих языков; б) сколько человек знают точно 2 языка; в) сколько человек знают только английский язык.

3. В коллективе 9 парней и 5 девушек. Сколько существует вариантов выбора делегации из 8 человек на собрание, если известно, что не менее половины делегации − парни.

4. Найти количество 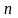-значных чисел, делящихся на 5, в записи которых есть точно 4 девятки и хоть одна пятерка.

5. Сколькими способами можно купить 6 фруктов, если киви продают по 0,1,3 шт., манго – 0,1,2 шт., авокадо – 0,2,4 шт., грейпфрут – 0,1,2 шт.

6. В автомашине семь мест. Сколькими способами семь человек могут расположиться в машине, если место водителя могут занять только трое из них ?

2 Вариант

1. Найти коэффициент при в разложении бинома .

2. В научном отделе работает 50 человек. Из них 25 человек знают английский язык, 13 – немецкий язык, 21 – итальянский язык, 5 – английский и немецкий, 9 – английский и итальянский, 3 – немецкий и итальянский; все три языка знают 3 человека. Определить: а) сколько человек не знают ни одного из этих языков; б) сколько человек знают точно 2 языка; в) сколько человек знают только немецкий язык.

3. В магазине имеются в наличии 9 различных книг Роберта Шекли и 11 различных книг Стивена Кинга. Сколько существует вариантов выбора покупки из 10 книг, если известно, что не менее половины книг Стивена Кинга, имеющиеся в наличии в магазине, вошли в покупку.

4. Найти количество -значных чисел, делящихся на 5, в записи которых есть хоть одна девятка и хоть одна пятерка.

5. Сколькими способами можно переставить цифры числа 1 234 114 546 так, чтобы никакие три одинаковые цифры не шли друг за другом?

6. Сколько различных аккордов можно взять на 10 выбранных клавишах рояля, если любое сочетание может состоять из 2, 3, … 7 звуков.

3 Вариант

1. Найти коэффициент при в разложении бинома .

2. В научном отделе работает 50 человек. Из них 13 человек знают английский язык, 19 – немецкий язык, 17 – итальянский язык, 3 – английский и немецкий, 2 – английский и итальянский, 8 – немецкий и итальянский; все три языка знает 1 человек. Определить: а) сколько человек не знают ни одного из этих языков?; б) сколько человек знают точно 2 языка?; в) сколько человек знают только итальянский язык?

3. В отделе 9 мужчин и 10 женщин. Сколько существует вариантов выбора делегации из 8 человек на собрание, если известно, что не менее половины мужчин отдела были на собрании.

4. Найти количество -значных чисел, делящихся на 5, в записи которых есть ровно две пятерки и хоть одна единица.

5. В ряд расположены п предметов. Сколькими способами можно выбрать из них три предмета так, чтобы не брать двух рядом стоящих предметов?

6. Пять девушек и трое юношей играют в городки. Сколькими способами они могут разбиться на две команды по 4 человека, если в каждой команде должно быть хотя бы по одному юноше ?