Обработка экспериментальной информации с использованием метода дисперсионного и корреляционно – регрессионного анализа
Большинство зависимостей свойств объекта получают эксперементально и представляют в виде таблиц и графиков.
При проведении анализа процессов возникает необходимость в статистической обработке опытных данных и представлении их в виде математических моделей, связывающих выходную и входную характеристику.
Для количественного выражения этой связи служит корреляционно–регрессионый анализ, включающий в себя:
корреляционный анализ – оценку тесноты связи параметров;
регрессионный анализ – определение формы и параметров уравнения регрессии;
анализ достоверности существования связи.
Дисперсионный анализ по полученным графикам позволяет выявить наиболее важные факторы и оценить степень их влияния.
По программе «Градуировка» получим расчет градуировочной таблицы уровнемера, в зависимости от параметров резервуара (изменяя только высоту днища). Построим два графика зависимости объема жидкости от высоты резервуара. Эксериментально установлено и повсеместно используются резервуары с высотой днища 400 мм, потому что при такой высоте работа нососов ничем не осложняна и используются насосы простейшей конструкции. Доказательства этого факта приведем методом корреляционно –регрессионного анализа.
Если изменить параметры резервуара, допустим изменить высоту днища на 600мм изменяться значения градуировочной таблицы, а соответственно и график., представленный на рисунке 2.49:
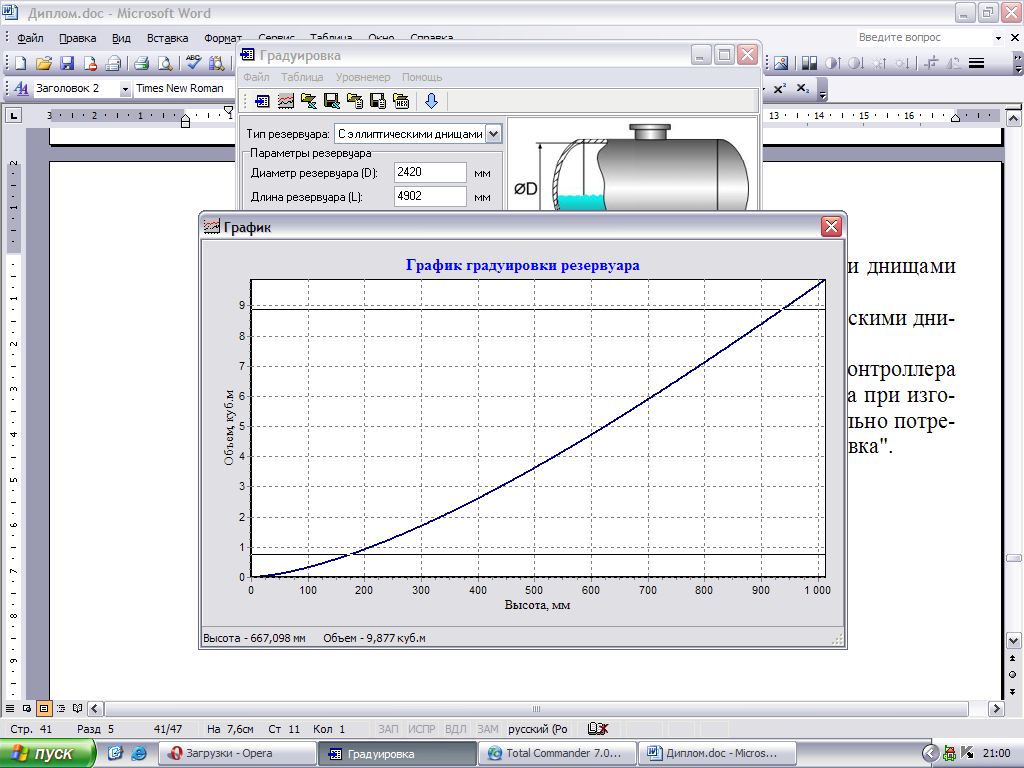
Рисунок 2.49 - Построение графика по результатам градуировочной таблицы про помощи программы «Градуировка» с высотой днища 400 мм
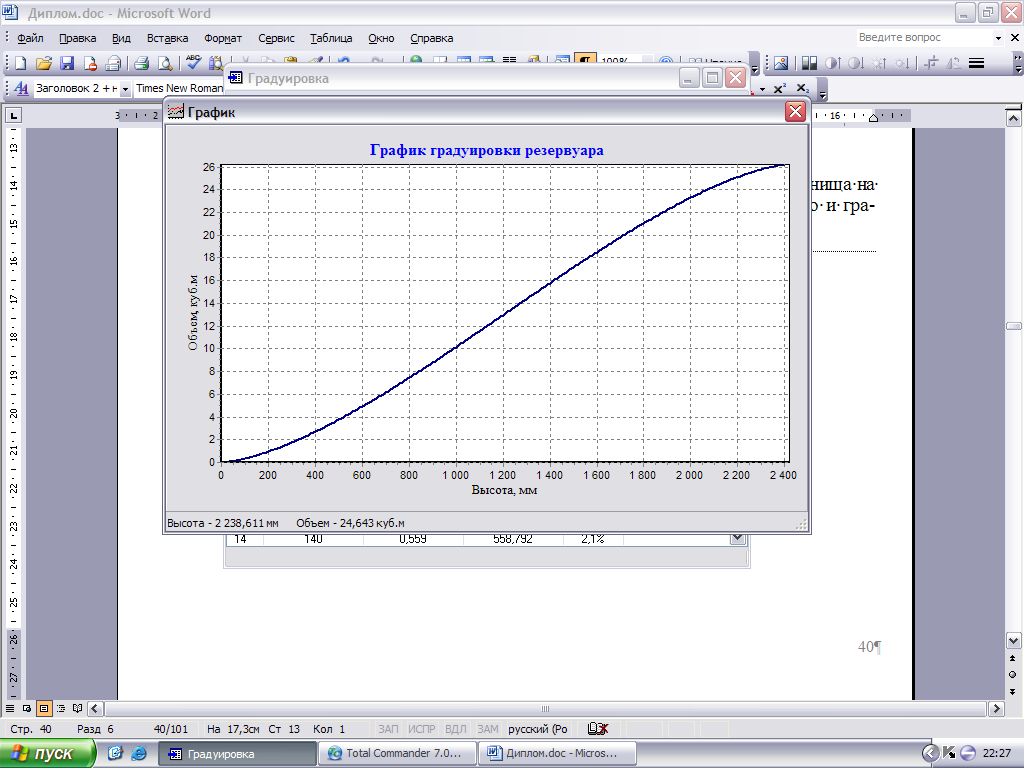
Рисунок 2.50 – График градуировочной таблицы при высоте днища 600 мм
В результате получены массивы двух величин объема жидкости и высоты резервуара, на которой этот объем будет зафиксирован.
Данные по расчету приведены в таблицах 2.6 и 2.7, а изображение математической модели приведено на графике, изображенном на рисунке 2.51.
Таблица 2.6 – Дисперсионный анализ
№ |
Наименование |
Оценка внутригрупповой дисперсии,
dis2 |
Оценка межгрупповой дисперсии,
dis1 |
F-критерий Фишера факт.,
Fp |
F-критерий Фишера теор.,
qF(1-α,f1,f2) |
Уровень значимости для F-критерия Фишера, α
|
1 |
График 1 |
1.333E+3 |
56306.76024 |
42.252 |
1.873 |
0.01 |
2 |
График 4 |
498.078 |
75041.25646 |
150.662 |
1.873 |
0.01 |
Таблица 2.7 – Корреляционно-регрессионный анализ
№ |
Математическая модель (ММ) |
Коэффиц. корреляции
rv |
Проверка значимости коэффициента корреляции |
Уровень значимости для критерия Стьюдента,
1-γ |
Остат. дисперия,
DISost |
Коэффициенты для ММ |
Среднее значение ошибки на интервале,
0/0 |
|
t-критерий Стьюдента факт.,
t_fact |
t-критерий Стьюдента теор.,
t_teor |
|||||||
1 |
|
0.99672 |
65.178 |
2.763 |
0.99 |
393.387 |
A0 = 3.721 A1 = 1.315 |
2.971 |
2 |
|
0.99923 |
135.05 |
2.763 |
0.99 |
138.007 |
A0 = 4.053 A1 = 1.228 |
1.254 |
