1. Синтез системы регулирования от переливания резервуаров

Система регулирования уровня жидкости состоит из заслонки (З), которая ограничивает подачу топлива в резервуар, преобразователя уровня жидкости в напряжение (ПУЖН) и измерительного моста (ИМ), с помощью которого определяется уровень топлива в резервуаре. Также в систему введены усилитель напряжения (УН), электродвигатель постоянного тока (ЭД), который приводит в движение редуктор (Р), для закрытия и открытия заслонки.

При открытии заслонки топливо поступает в резервуар. При заполнении резервуара топливом до критического значение, на магнитострикционном преобразователе уровня (МПУЖ) срабатывает сигнал о предельном значении уровня и подается сигнал об запрете подачи топлива, путем подачи напряжения на измерительный мост, затем напряжение поступает на усилитель напряжения, которое усиливается и приводит в движение электродвигатель постоянного тока малой мощности. Двигатель приводит в движение редуктор, который закрывает или открывает заслонку, тем самым ограничивает налив топлива.

Схема системы регулирования приведена на рисунке 2.21

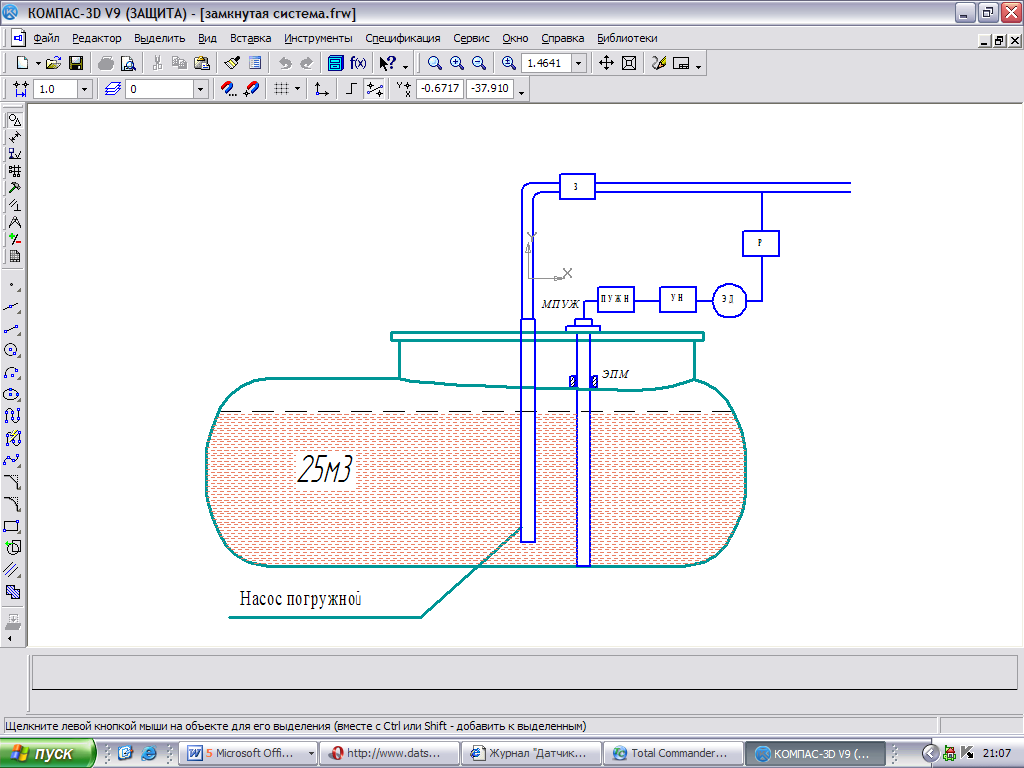
Рисунок 2.21 – Система регулирования уровня топлива в резервуаре

Математическое описание элементов системы:

1. Резервуар:

.

2. Магнитострикционный преобразователь уровня жидкости:

.

3. Электрический мост:

.

4. Усилитель напряжения:

.

5. Двигатель постоянного тока малой мощности:

;

.

6. Редуктор:

Передаточные функции:

1) Резервуар:

.

2. Магнитострикционный преобразователь уровня жидкости:

.

3) Электрический мост:

.

4. Усилитель напряжения:

.

4. Двигатель постоянного тока малой мощности:

4. Редуктор:

.

На основании уравнений составляем структурную схему:

Мн

x δ H u Uy ω x

Рисунок 2.22 - Структурная схема регулирующей системы

Преобразуем схему в эквивалентную одноконтурную систему:

f

f

и

Передаточная функция разомкнутой системы имеет вид:

.

90	0,02	0,2	3	0,002	0 ,001	100	0,9	50

= ;

Характеристическое уравнение системы имеет вид:

Определение передаточных функций:

1) Передаточная функция разомкнутой системы:

;

2) Передаточная функция замкнутой САР относительно задающего воздействия:

;

3) Передаточная функция замкнутой САР по ошибке от задающего воздействия:

.

Исследование на устойчивость

Определим устойчивость разомкнутой системы по критерию Гурвица.

Характеристическое уравнение имеет вид:

.

По критерию Гурвица для устойчивости системы 4 порядка должны удовлетворять следующие неравенства:

С₀ > 0; С₁ > 0; С₂ > 0; С₃ > 0; С₄ > 0.

С₁С₂С₃–С₀С₃²–C₁²C₄>0, где - коэффициенты характеристического уравнения.

;

;

С₀=0,0063> 0; С₁ =6,3> 0; С₂ =0,16> 0; С₃ =90> 0; С₄ =1> 0;

С₁С₂С₃–С₀С₃²–C₁²C₄=90,721008-51,03-39,6908=0.

Так как все коэффициенты, но один определитель равен нулю, то по критерию Гурвица разомкнутая система находится на границе устойчивости.

Произведем расчет и построение годографа разомкнутой САУ и определим устойчивость замкнутой системы по критерию Найквиста:

.

Используем подстановку p = jw и раскроем скобки:

P(w)+jM(w);

;

.

Подставляем значения в таблице 2.2 , получаем:

Таблица 2.2

W	P(w)	M(w)
0	9	0
0,005	7,484432	-3,368
0,01	4,972415	-4,47521
0,02	2,122661	-3,82093
0,05	0,423517	-1,90626
0,1	0,109737	-0,98852
0,2	0,027671	-0,49987
0,5	0,00442	-0,20347
0,7	0,002244	-0,1479
1	0,001087	-0,10752
10	1,48E-05	0,001667
11	1,22E-05	0,001217
3,7	-0,00045	-0,6483
3,77	-0,0043	-5,21539
3,79	0,004111	4,798905
3,9	0,000416	0,396234

Строим АФЧХ разомкнутой системы, результат представлен на рисунке 2.23:

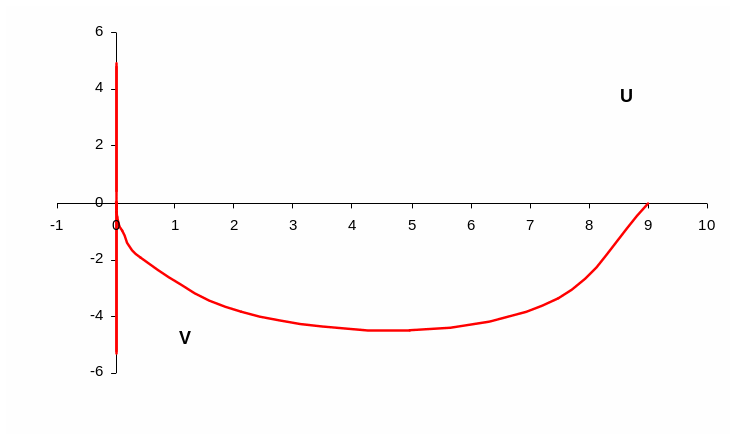
Рисунок 2.23 – АФЧХ разомкнутой системы

По графику видно, что разомкнутая система находиться на границе устойчивости.

Так как характеристическое уравнение имеет пару мнимых корней, то по критерию Найквиста для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы при изменении w от 0 до ∞ дополненная на участке разрыва дугой бесконечного радиуса ,не охватывала точку с координатами (-1;j0). Судя по графику данный дополненный радиус охватывает точку (-1;j0), значит замкнутая система не устойчива.

Расчет и построение ЛАЧХ и ЛФЧХ и определение устойчивости замкнутой системы по логарифмическому критерию Найквиста.

, следовательно, передаточный коэффициент: К = 9, порядок астатизма Θ = 0

Сопрягающие частоты будут следующими:

;

;

.

Построим низкочастотную асимптоту ЛАЧХ: так как Θ = 0, то ее наклон 0 дБ/дек и ордината низкочастотной части ЛАЧХ равна 20 lg 9 = 19 и низкочастотную асимптоту доводим до первой сопрягающей частоты .

На всех сопрягающих частотах наклон ЛАЧХ изменяется:

От до наклон ЛАЧХ будет -20 Дб/дек, так как сопрягающая частота создана полиномом знаменателя 1 порядка. От до наклон ЛАЧХ будет -60 дБ/дек, так как создан полиномом знаменателя 2 порядка. На высокочастотной части от до ∞ наклон ЛАЧХ будет - 80 Дб/дек.

Используя таблицы поправок находим поправки на сопряженных частотах.

Построим ЛФЧХ разомкнутой системы. Степень астатизма равно 0, значит составляющие суммируются относительно прямой 0, нахождение составляющих соотвующих сопрягающим частотам используют таблицы «Логарифмические фазочастотные характеристики полиномов».

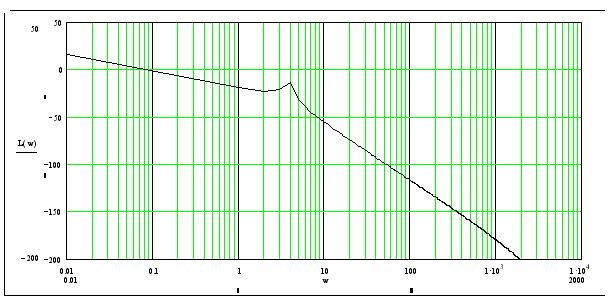
Рисунок 2.24 – График ЛАЧХ разомкнутой системы

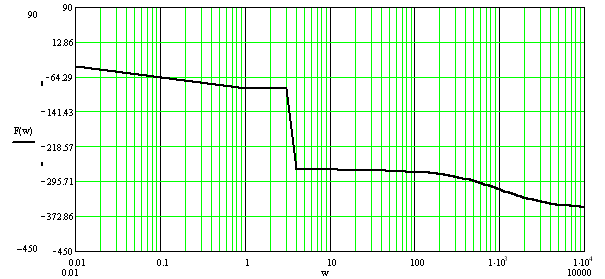
Рисунок 2.25 – График ЛФЧХ разомкнутой системы

По логарифмическому критерию, если разомкнутая система находится на границе устойчивости, то для устойчивости замкнутой системы необходимо и достаточно чтобы при положительной ЛАЧХ число пересечений ЛФЧХ уровня снизу вверх «+» должно быть на раз больше числа пересечений в обратном направлений «-» , где - число правых корней характеристического уравнения разомкнутой системы. Т.к. из характеристического уравнения разомкнутой системы = 0, то разность пересечений должно равно 0, судя по графику ЛАЧХ исходит из точки то есть имеется половина перехода, значит, замкнутая система неустойчива.

Построение желаемой ЛАЧХ

Требуется построить желаемую ЛАЧХ при следующих данных:

δ	σ, %	,град	,с
10	30	45	100	1	0,01

По заданным параметрам строим запретную зону, куда не должна заходить желаемая ЛАЧХ. Величины ω_к и L_к определяют из следующих соотношен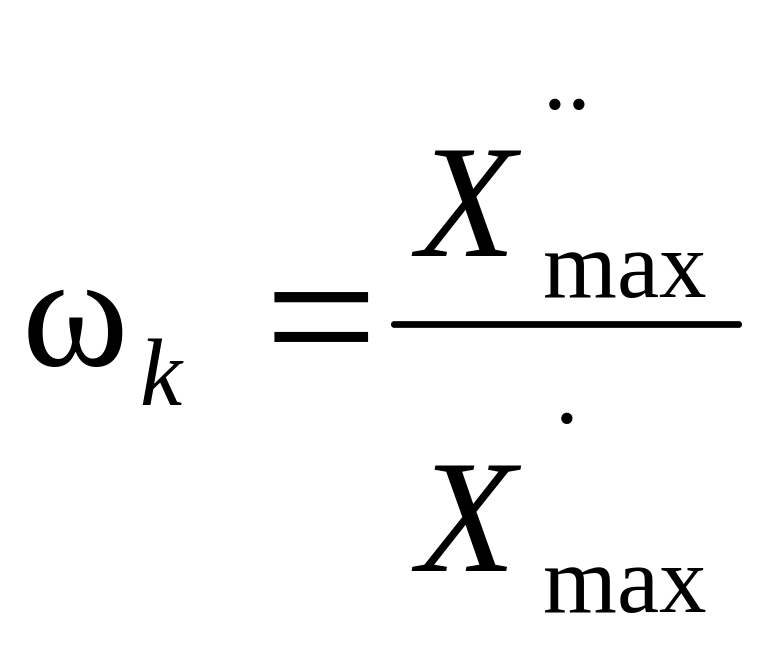ий:

и .

и

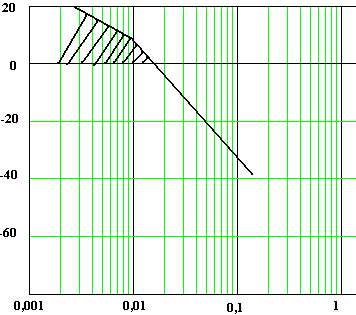
Рисунок 2.26 – Запретная зона желаемой ЛАЧХ

Так как максимальное ускорение не велико выбираем типовое ЛАЧХ типа: ;

Определяем необходимое значение запаса устойчивости по фазе.

γ = 73-10=63.

Определим частоту среза по формуле:

т.к. γ = 63, то с = 7;

.

Принимаем, что сопрягающую частоту создает постоянная времени 90 с неизменяемой части системы:

.

По соотношению из таблицы, определим:

Возьмем k = 9,тогда:

;

Вычисляем постоянную в радианах:

;

Примем, что постоянные времени 0,265 и 0,001с неизменяемой части создают сопрягающие частоты и ;

По формуле , определим сопрягающую частоту ω₃:

Для проверки расчета составим левую и правую части приближенного равенства:

;

.

Можно считать, что расчет выполнен правильно. Таким образом, передаточная функция системы, имеющей желаемую ЛАЧХ имеет вид:

;

.

Выбор корректирующего устройства

Из построенных графиков ЛАЧХ и ЖЛАЧХ найдем разность, т.е. ЛАЧХ последовательного корректирующего устройства:

.

По графику определим передаточную функцию: ;

;

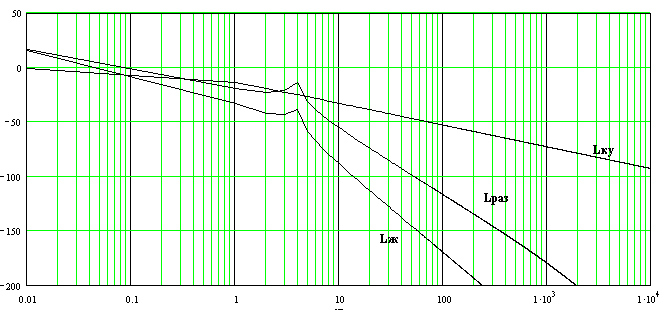
Рисунок 2.27 – ЛАЧХ и ЛФЧХ корректирующего устройства L_k(w), желаемой L_ж(w) и L_н(w) неизменяемой части системы

Выберим типовую корректирующее устройство по справочным данным, т.к. передаточная функция сложная разобьем на типовые корректирующие устройства: