Типы задач:

1. Расчёт курса, скорости и времени по известному ветру.

Рассмотрим порядок решения задачи на примере со следующими исходными данными:

V = 400;

ЗМПУ =232;

δ =290;

U = 70;

S = 164;

ΔМ= –4.

Необходимо найти:

- магнитный курс, при выдерживании которого ВС будет лететь по ЛЗП;

- путевую скорость;

- время полета на участке маршрута.

Решение задачи

1. Рассчитывается навигационное направление ветра:

δ_н = δ ± 180 °– ΔМ = 290 – 180 – (–4) = 114.

2. Рассчитывается угол ветра.

УВ= δ_н –ЗМПУ = 114 – 232 = – 118 = 242.

Очевидно, что при таком УВ ветер дует влево и назад относительно направления полета. Следовательно, УС должен быть отрицательным (будет сносить влево), а путевая скорость получится меньше истинной.

3. Находят угол сноса и путевую скорость с использованием теоремы синусов (3.8). Из нее следует:

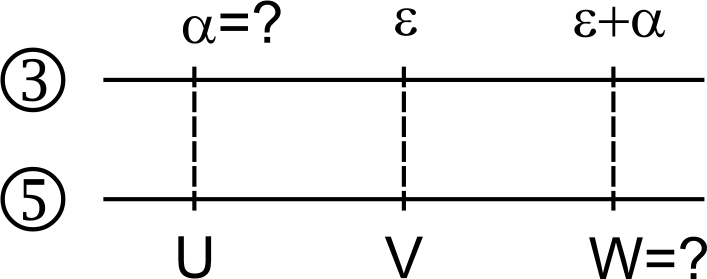
КУВ=УВ+УС;

.

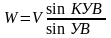Расчет по этим формулам можно выполнить как на калькуляторе, так и на НЛ-10М.

Угол сноса равен –9°.

КУВ = 242 + (–9) = 233.

Путевая скорость 362 (округлено до одного км/ч). \

4. Рассчитывают курс следования, который обеспечит выполнение полета по ЛЗП.

МК=ЗМПУ–УС.

МК=232– (–9)=241.

5. Рассчитывают время полета на участке.

.

При расчете на калькуляторе непосредственно по этой формуле время будет получено в часах, поскольку W измеряется в километрах в час. Чтобы получить время (как это требуется) в минутах, необходимо полученный результат умножить на 60 (количество минут в часе).

На НЛ-10М расчет времени выполняется с помощью ключа (см. рис.4.8), по которому время получается в минутах.

2. Определение ветра в полёте.

Дано:

V=680;

W=590;

МК=312;

УС=+8;

ΔМ= –4.

Найти: δ_н , δ, U.

Решение:

1. Находим эквивалентный ветер:

U_экв = W – V =590-680= –90 км/ч.

2. На НЛ-10М находим по ключу на рис. 3.12 острый угол ветра ε^* и скорость ветра U:

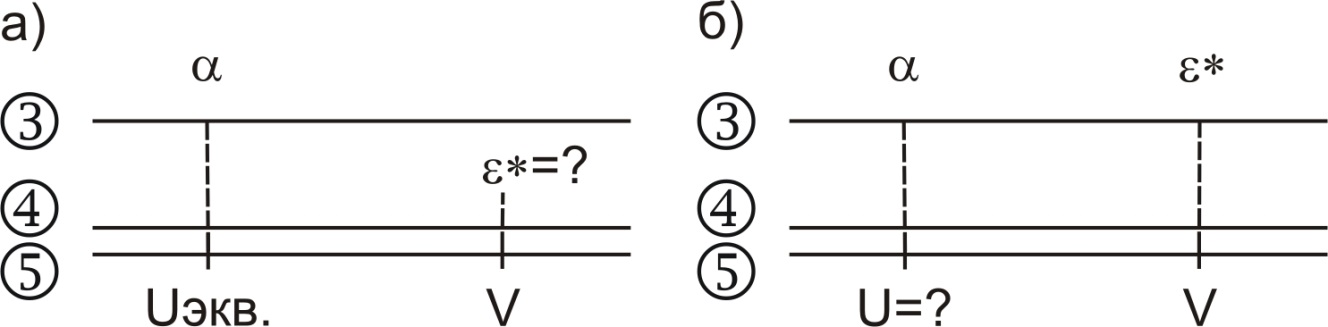
Рис. 3.12. Определение ветра

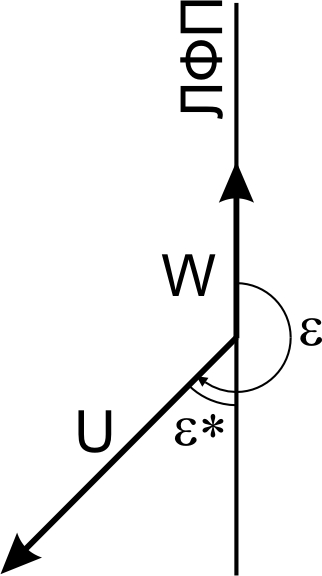
Рис. 3.13. Угол ветра и острый угол ветра

U=130 км/ч, ε^*=46°.

3. Находим ФМПУ:

ФМПУ=МК+УС=312+8=320°.

4. Поскольку W<V, то ветер дует назад, а так как УС>0, то ветер дует вправо. Следовательно, вектор ветра лежит во II четверти, если отсчитывать четверти от направления ЛФП по часовой стрелке (см.рис. 3.14). В этом случае острый угол ветра ε^* отсчитывается от направления, противоположного направлению W, то есть:

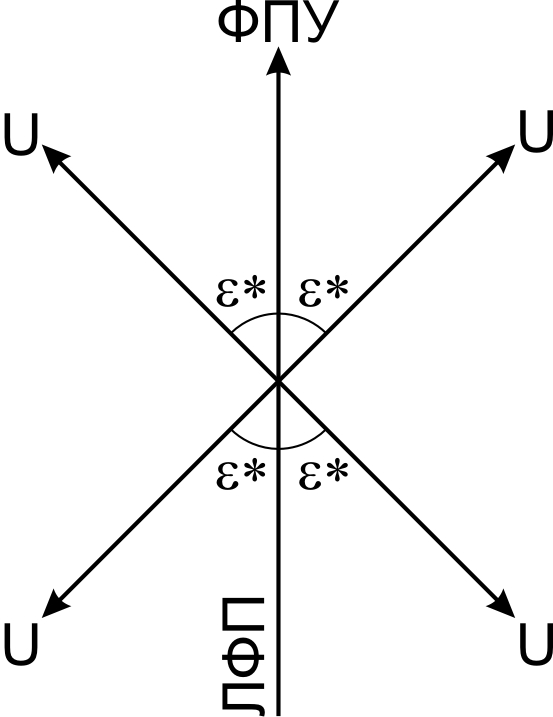
Рис. 3.14. Возможные направления ветра относительно ЛФП

ФМПУ±180 = 320 –180=140°.

Поскольку вектор ветра расположен от этого направления в сторону против часовой стрелки, то направление ветра будет меньше на величину ε^* :

δ_н =140 – 47 = 93°.

5. Метеорологическое направление ветра:

δ= 93+180 – 4=269°.

3. Преобразование курса.

От Ивана Мало Каши.

4. Расчёт истинной скорости по широкой стрелке.

Истинная скорость по показанию широкой стрелки КУС рас­считывается по формуле:

V_и = V_пр + ΔV_и + ΔV_a + ΔV_сж + ΔV_м,

где V_пр – показание широкой стрелки (приборная скорость);

ΔV_и – инструментальная поправка;

ΔV_a – аэродинамическая поправка;

ΔV_cж – поправка на изменение сжимаемости воздуха;

ΔV_м – методическая поправка на изменение плотности воздуха.

Пример . Барометрическая высота H = 8600 м; показание широкой стрелки V_пр=500 км/ч; ΔV_и = + 8 км/ч; ΔV_а = − 30 км/ч; показание термометра наружного воздуха на высоте полета t_пр = −38°. Определить истинную воздушную скорость.

Решение. 1. Находим величину поправки на изменение сжимаемости (см. табл. 7.1). При этом учитываем, что эта поправка всегда отрицательна. При необходимости интерполируем эту поправку в таблице по высоте и скорости. Получаем ΔV_сж = −19 км/ч.

2. Рассчитываем величину приборной исправленной скорости:

V_{пр. испр} = 500 + (+ 8) + (− 30) + (− 19) = 459 км/ч.

3. Для учета поправки на изменение плотности воздуха необходимо знать фактическую температуру на высоте t_H, для чего необходимо ввести поправку Δt в показания термометра t_пр. Но величина этой поправки (см. табл.7.2) и на шкале 16 НЛ-10М указана в зависимости от истинной скорости, которая неизвестна. Ведь именно она и должна быть получена в результате решения данной задачи. Получается замкнутый круг: для определения точного значения истинной скорости необходимо знать истинную скорость. На самом деле для определения поправки к термометру достаточно знать приближенную истинную скорость, хотя бы ее «грубое» значение. Обычно оно известно экипажу из опыта полетов. Если же нет, то приближенная истинная скорость может быть получена одним из следующих способов:

- по показаниям узкой стрелки КУС, которая и показывает приближенную истинную скорость;

- путем расчета в уме;

- путем расчета по неточной приборной температуре термометра.

В данном примере воспользуемся последним из перечисленных способов. Находим примерное значение истинной воздушной скорости Ṽ_и используя ключ на рис. 7.10, но вместо неизвестной пока t_Н подставляем t_пр . Получаем Ṽ_и = 735 км/ч.

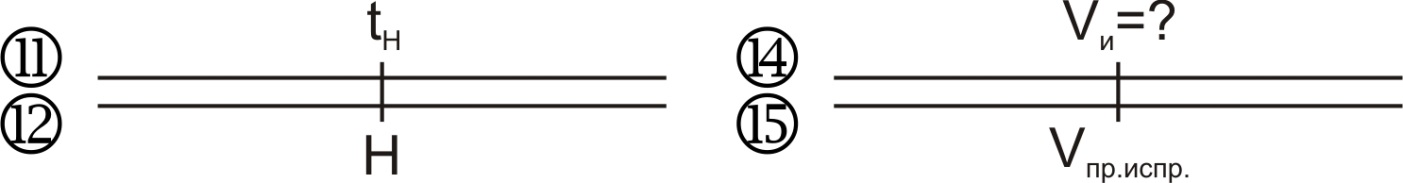
Рис. 7.10. Учет методической поправки на изменение плотности воздуха

4. Определяем поправку к показанию термометра наружного воздуха и фактическую температуру воздуха на высоте полета:

t_Н = t_пр - Δt.

В данном примере для Ṽ_и =735 км/ч получим из табл. 7.2 (или по шкале 16 НЛ-10М) Δt = 14°. Следовательно, t_н = −38 −14 = −52°. Для избежания ошибок необходимо обращать внимание на то, чтобы фактическая температура оказалась ниже (холоднее) приборной.

5. Используя теперь уже фактическую температуру t_н = −52°, рассчитываем по тому же ключу (см. рис. 7.10) истинную скорость: V_ист = 705 км/ч.

5. Контроль пути при полёте на/от радиостанции и исправление пути с углом выхода.

Вопрос 28,29,31.

6. Определение путевой скорости и угла сноса на контрольном этапе.

Вобщем я заебался, сами найдите ответ.

7. Определение места самолёта по двум радиостанциям (или VOR, или АРП).

Вопрос 30.

8. Полная прокладка.

Вопрос 16.

9. Штилевая прокладка.

Вопрос 16.

10. Определение МС по БРЛС угломерно-дальномерным способом.

Вопрос 41.