Параметры, определяемые с помощь инс. Бесплатформенные инс.
Параметры, определяемые с помощью ИНС. Инерциальные системы предназначены для определения координат места самолета. Но в процессе их определения можно получить значения многих других параметров, необходимых для навигации. Перечислим основные из этих параметров и рассмотрим, каким образом они могут быть получены.
1. Курс, крен и тангаж. Это параметры, определяющие угловое положение самолета относительно трех осей. В традиционных ИНС гироплатформа стабилизирована по меридиану и в горизонтальной плоскости, поэтому не составляет труда определить угловое положение ВС относительно гироплатформы, то есть три перечисленных параметра. В бесплатформенных системах эти параметры рассчитываются путем интегрирования угловых скоростей.
ИНС непосредственно измеряет истинный курс, то есть курс относительно текущего географического меридиана. Но, поскольку текущие счисленные координаты всегда известны, вычислитель ИНС (или центральный вычислитель навигационного комплекса самолета) может рассчитать и ортодромический курс относительно любого опорного направления.
В памяти современных ИНС хранится модель магнитного поля Земли, с помощью которой вычислитель может рассчитать магнитное склонение в точке расположения самолета. Тогда система может определить и магнитный курс, вычтя магнитное склонение из измеренного истинного курса.
У современных БИНС погрешности определения крена и тангажа составляют 0,05-0,1°, а истинного курса около 0,4°. Погрешность определения магнитного курса зависит еще и от точности модели магнитного поля и составляет порядка 1-1,5°.
2. Угловые скорости изменения курса, крена, тангажа. В бесплатформенных системах эти параметры непосредственно измеряются лазерными гироскопами (с погрешностью порядка 0,1º в секунду), а в традиционных ИНС при необходимости могут быть получены расчетным путем.
3. Ускорения самолета по трем перпендикулярным осям. В традиционных ИНС ускорения измеряются по осям земной системы координат (на север, на восток, вверх), а в БИНС – по строительным осям ВС (вперед, вправо, вверх) и затем пересчитываются в земную систему координат. Значения ускорений нигде не индицируются, а только используются для дальнейших расчетов.
4. Скорости перемещения ВС по трем осям земной системы координат: на север WN, на восток WE, вверх Wверт . Разумеется, скорости, как и ускорения могут быть фактически быть направлены и на юг, запад, вниз – это отразится в знаке перечисленных скоростей. Погрешности определения горизонтальных составляющих скорости составляют единицы километров в час, а вертикальной скорости порядка 0,2 м/с.
5. Путевая скорость W. Поскольку составляющие путевой скорости известны, то и путевая скорость (рис. 8.28) может быть определена по формуле:
.
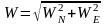6. Фактический путевой угол βФ. Фактический истинный путевой угол (см. рис. 8.28), может быть определен по формуле:
.
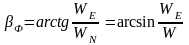Путем вычитания магнитного склонения может быть получен и магнитный путевой угол.
7. Угол сноса α. Поскольку фактический путевой угол βФ и курс γ известны, то в соответствии с навигационным треугольником скоростей
α= βФ – γ.
8. Географические координаты места самолета. В простейшем случае, если принять Землю за сферу, то по составляющим путевой скорости могут быть рассчитаны сферические широта φ и долгота λ места самолета по формулам (8.6). В вычислителе может быть запрограммирован алгоритм учета поправок в координаты за счет сжатия Земли или алгоритм расчета координат на поверхности земного эллипсоида. Возможно, в этом и нет особой необходимости. Ведь требуемая международными документами точность определения счисленных координат с помощью ИНС, которая и реализована в современных системах, составляет 1 морскую милю (1,852 км) за час полета, а поправки за счет сжатия Земли имеют гораздо меньшую величину.
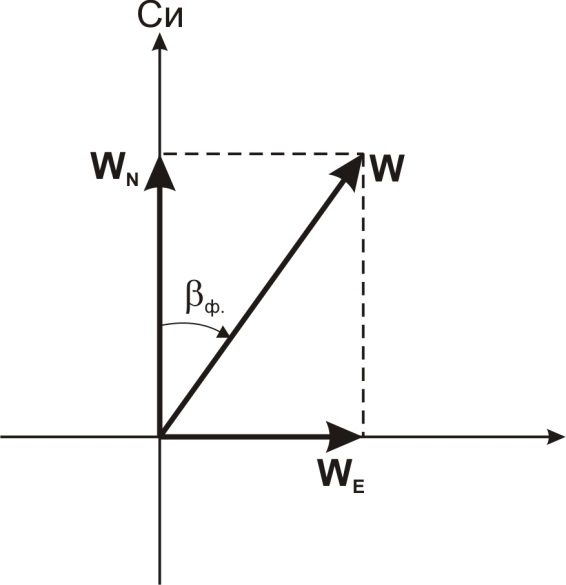
Рис. 8.28. К определению W и ФПУ
9. Высота полета. Высота является третьей пространственной координатой и, как и горизонтальные координаты (φ и λ), может быть рассчитана с помощью ускорения, измеряемого вертикальным акселерометром. Полученная таким образом высота, называемая иногда инерциальной высотой, имеет такой же порядок точности как и горизонтальные координаты. Разумеется, для высоты это совершенно неудовлетворительная точность и поэтому инерциальная высота пока не используется в навигации ни для эшелонирования, ни для предотвращения столкновений с препятствиями. Но она может использоваться в алгоритмах работы самой ИНС. Например, для расчета радиуса Земли с учетом высоты полета, необходимого для определения положения текущей горизонтальной плоскости.
Можно видеть, что перечисленный список определяемых ИНС параметров включает в себя почти все величины, необходимые для навигации. Тем не менее, ИНС самостоятельно не может определить, например, скорость и направление ветра, поскольку для этого необходимо знать еще и истинную воздушную скорость, которую система не измеряет. Для расширения возможностей современных ИНС на вход их вычислителей подается информация от других бортовых систем. Например, от системы воздушных сигналов может поступать истинная воздушная скорость и барометрическая высота. В этом случае возможно и определение ветра.
Вычислитель, входящий в состав ИНС, предназначен для решения своих специфических задач: определения счисленных координат и других параметров. Он имеет и необходимую для своей работы память. Но почему бы не «загрузить» этот вычислитель и память дополнительными функциями, полезными для навигации?
Даже первые образцы используемых в гражданской авиации ИНС имели возможность ввести в память географические координаты нескольких ППМ. Тогда появляется возможность определения еще целого ряда параметров. Например, следующих:
- заданного путевого угла и длины участка маршрута. Поскольку координаты начального и конечного ППМ каждого участка маршрута известны, можно математически рассчитать длину и направление ортодромической ЛЗП;
- линейного бокового уклонения и оставшегося до ППМ расстояния. Эта задача тоже решается чисто математически, поскольку координаты ВС и ППМ участка известны;
- оставшегося времени полета до ППМ и гринвичского времени его пролета;
- поправки в фактический путевой угол для выхода в ППМ,
а также других параметров. Разумеется, не во всех ИНС эти функции реализованы в полном объеме. В них нет необходимости, если эти же задачи решает центральный вычислитель навигационного комплекса, в который входит ИНС как один из датчиков.
Бесплатформенные инерциальные навигационные системы
На протяжении многих десятилетий усилия инженеров, разрабатывавших традиционные ИНС, были направлены на уменьшение собственного ухода гироскопов, удерживающих гироплатформу в заданном положении. Непрерывное совершенствование конструкции, меры по уменьшению трения в осях кардановых подвесов и даже изобретение новых видов гироскопов (ядерных, с жидкостным ротором и др.) делали ИНС все дороже и сложнее, но не приводили к существенному повышению их точности.
В начале 60-х годов был изобретен принцип работы так называемых лазерных гироскопов, широкое внедрение которых (спустя 20-30 лет) позволило решить многие проблемы. «Лазерный гироскоп» − не корректное название, поскольку это устройство вовсе не является гироскопом, в нем нет быстровращающихся частей. Называется он так только потому, что предназначен для решения той же задачи, для которой предназначен гироскоп в традиционной ИНС, – определения направлений в пространстве (верх-низ, север-юг, восток-запад) независимо от углового положения ВС.
ИНС, основанные на использовании лазерных гироскопов, называют бесплатформенными инерциальными системами (БИНС), поскольку в них отсутствует гироплатформа, которую необходимо удерживать в требуемом положении. Акселерометры в таких системах жестко закреплены на самолете и направлены по его строительным осям (вперед, вправо, вверх).
Кольцевой лазерный гироскоп представляет собой сложный квантовый оптико-механический прибор, включающий в себя лазер, систему зеркал и управляющие электронные системы.
Оптический квантовый генератор или лазер (англ. laser, сокр. от Light Amplification by Stimulated Emission of Radiation − усиление света посредством вынужденного излучения), — это устройство, использующее квантовомеханический эффект вынужденного излучения для создания когерентного, монохроматического, поляризованного и узконаправленного потока излучения. В отличие от обычного источника света, излучающего обычно целый спектр частот, лазер излучает на строго определенной частоте.
Лазерный гироскоп называется кольцевым, поскольку луч в нем, отражаясь от зеркал, проходит по замкнутому контуру в форме квадрата или треугольника (рис. 8.24).
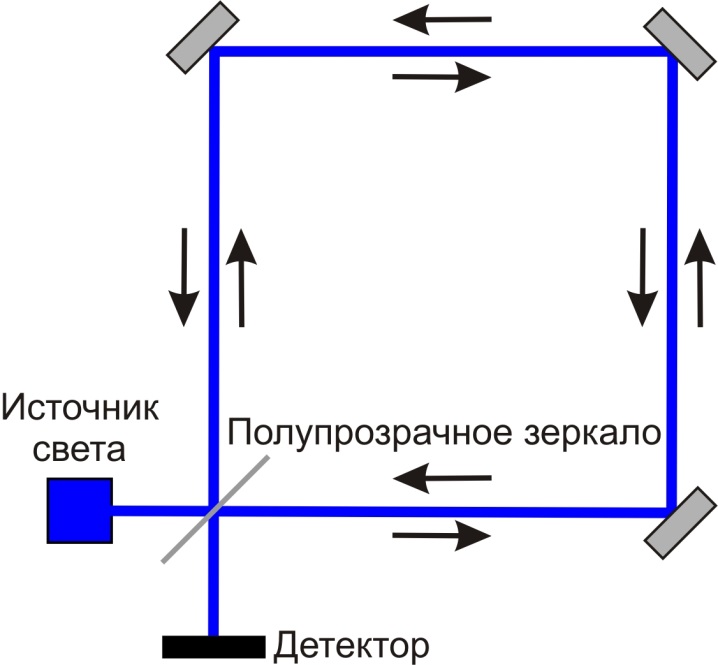
Рис. 8.24. Лазерный гироскоп
По кольцевому контуру проходят два луча лазера в противоположных направлениях навстречу друг другу. Если вся эта система лазера и зеркал неподвижна в инерциальной системе отсчета, то частоты обоих лучей, воспринимаемые детектором, будут одинаковы. Но если эта система будет вращаться вокруг оси, перпендикулярной плоскости траектории лучей, то измеряемые частоты лучей вследствие эффекта Доплера будут различаться, причем, тем сильнее, чем больше угловая скорость вращения. Таким образом, с помощью лазерного гироскопа можно измерить угловую скорость вращения. В БИНС используется три таких лазерных гироскопа, измеряющих угловые скорости вращения вокруг трех перпендикулярных осей (рис. 8.25).
Рис. 8.25. Моноблок из трех взаимно перпендикулярных треугольных лазерных гироскопов
Поскольку в любой момент времени известна угловая скорость, то в любой момент можно рассчитать угол, на который повернулась система по сравнению с первоначальным положением. Ведь угловая скорость – производная (скорость изменения) угла поворота. Следовательно, сам угол можно определить путем интегрирования угловой скорости. Осуществляется как бы счисление угла поворота. Эту задачу непрерывно решает вычислитель БИНС.
Если в начальный момент времени было известно, как направлены строительные оси ВС и ориентированные по ним акселерометры по отношению к земной системе координат (к горизонтальной плоскости, к направлению на север), то по рассчитанным углам поворота можно определить их ориентацию в любой текущий момент времени. Остается только пересчитать измеренные ускорения в связанную с Землей и повернутую относительно ВС прямоугольную систему координат. Таким образом, как и в традиционных ИНС, оказываются известными значения ускорений по направлениям север-юг, восток-запад, верх-низ.
Отсутствие в БИНС гироплатформы, вращающихся гироскопов и связанных с ними проблем позволило сделать это устройство более компактным (рис. 8.26). Дальнейшее совершенствование техники и технологии сделали БИНС и более дешевыми, и более точными. Достижение еще более высокой точности лазерных гироскопов сдерживается пока явлением «захвата лучей», то есть взаимодействием встречных лучей, которое приводит к рассеиванию света.
Вполне вероятно, что стремительное развитие научно-технического прогресса приведет к внедрению новых систем, основанных на пока не используемых в авиации принципах. Например, уже разработаны компактные датчики ускорений и вращений, основанные на применении электрически заряженной жидкости с ферромагнитными свойствами (рис. 8.27).
Рис. 8.26. Отечественный лазерный гироскоп КМ-11-1А
(фактический диаметр около 1,3 см)
Рис. 8.27. Датчик ускорений и углов поворота по трем осям