12.3. Розрахунок кіл з несинусоїдними електрорушійними силами і струмами

Розрахунок електричних кіл з несинусоїдними е.р.с. проводять у такій послідовності.

1. Несинусоїдна е.р.с. розкладається в гармонічний ряд:

е = Е0 + e1 + e2 + e3 + … .

(12.10)

2. Джерело несинусоїдної е.р.с. розглядається як послідовне з'єднання джерела постійної е.р.с. Е₀ і джерел синусоїдних е.р.с. з різними частотами (рис.12.4).

3. Розрахунок кола ведеться для кожної гармоніки окремо:

Е0	I0
;	;
;	;
;	,
і т.д.

4. Використовуючи принцип суперпозиції, знаходять загальний несинусоїдний струм:

i = I0 + i1 + i2 + i3 + … .

(12.11)

Закон Ома для k-й гармоники записывается так:

.

(12.12)

Если мгновенное значение напряжения задано для k-й гармоники, то мгновен­ное значение тока может быть записано в общем виде:

;
;
.

При расчётах каждой из гармоник можно пользоваться символическим (ком­плексным) методом и строить векторные диаграммы для каждой из них отдельно. Но недопустимо производить геометрическое сложение векторов и комплексов напряжений с токами разных гармоник.

Пример 12.1

Найти мгновенное значение тока в цепи, если известно: u = 200 sinωt + 100 sin 3ωt, r = 6 Ом, L = 25,5 мГн, f = 50 Гц.

Решение.

1. Составляем расчётную схему цепи (рис.12.5).

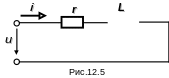
2. Находим ток первой гармоники:

;

;

,

где

ωL = 314 ∙ 25,5 ∙ 10 ^{– 3} = 8 Ом;

Закон Ома для k-ої гармоніки записується так:

.

(12.12)

Якщо миттєве значення напруги задане для k-ої гармоніки, то миттєве значення струму може бути записане в загальному вигляді:

;
;
.

При розрахунках кожної з гармонік можна користуватися символічним (комплексним) методом і будувати векторні діаграми для кожної з них окремо. Але неприпустимо робити геометричне додавання векторів і комплексів напруг зі струмами різних гармонік.

Приклад 12.1

Знайти миттєве значення струму в колі, якщо відомо: u = 200 sinωt + 100 sin 3ωt, r = 6 Ом, L = 25,5 мГн, f = 50 Гц.

Рішення.

1. Складаємо розрахункову схему кола (рис.12.5).

2. Знаходимо струм першої гармоніки:

;

;

,

де

ωL = 314 ∙ 25,5 ∙ 10 ^{– 3} = 8 Ом;

;

.

3. Находим ток третьей гармоники:

;

;

,

где

;

.

4. Находим мгновенное значение несинусоидального тока:

.

12.4. Мощность и коэффициент мощности при несинусоидальных токах

Активная мощность периодического переменного тока какой-либо формы находится как среднее значение мощности за период:

.

(12.13)

Если мгновенные значения напряжения и тока записать в виде рядов Фурье, то в этом случае получим:

,

т.е.

.

(12.14)

Таким образом, активная мощность несинусоидального тока равна сумме ак­тивных мощностей отдельных гармоник.

По аналогии с синусоидальными токами вводится понятие полной мощности:

S = UI,

;

.

3. Знаходимо струм третьої гармоніки:

;

;

,

де

;

.

4. Знаходимо миттєве значення несинусоїдного струму:

.
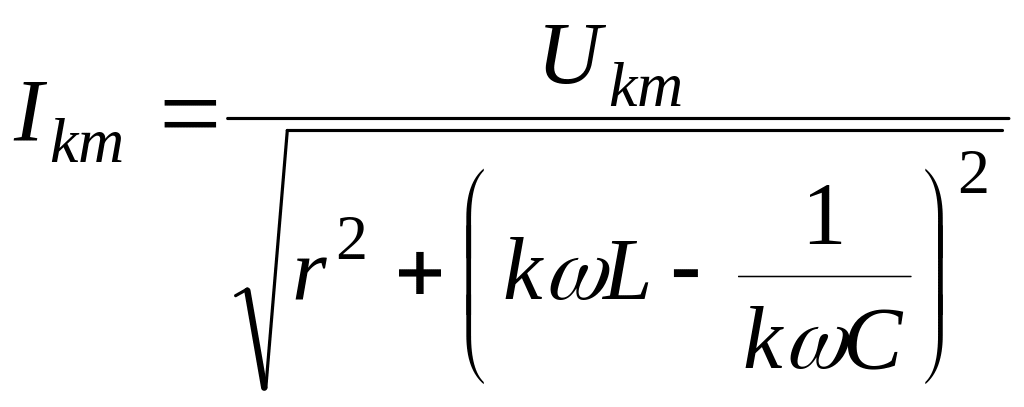