Тема 12. Несинусоидальные токи

12.1. Несинусоидальные периодические токи и их представление в виде тригонометрического ряда

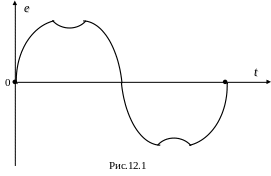
До сих пор мы рассматривали линейные цепи переменного тока с синусои­дальными э.д.с. Но на практике э.д.с. и токи довольно часто отличаются от сину­соидальных. Например, в генераторах переменного тока вследствие того, что ин­дукция распределяется в теле статора не по синусоидальному закону, э.д.с., кото­рые наводятся в обмотках, также несинусоидальны (рис.12.1).

Явления, которые происходят в линейных цепях при периодических, но неси­нусоидальных э.д.с. или токах, проще всего исследовать, если э.д.с. или токи раз­ложить в тригонометрический ряд Эйлера-Фурье:

,

(12.1)

где при k = 0, А_km = А₀, а φ_k = ψ₀ = 90º.

Первый член ряда А₀ называется постоянной составляющей или нулевой гар­моникой, второй член – основной синусоидой или первой гармони­кой, а все последние члены вида при k > 1 носят назва­ние высших гармоник.

Тригонометрический ряд после преобразования синуса суммы каждой гар­моники можно еще записать так:

(12.2)

где .

Тема 12. Несинусоїдні струми

12.1. Несинусоїдні періодичні струми та їх уявлення у вигляді тригонометричного ряду

Досі ми розглядали лінійні кола змінного струму із синусоїдними е.р.с. Але на практиці е.р.с. і струми досить часто відрізняються від синусоїдних. Наприклад, у генераторах змінного струму внаслідок того, що індукція розподіляється в тілі статора не за синусоїдним законом, е.р.с., які наводяться в обмотках, також несинусоїдні (рис.12.1).

Явища, які відбуваються в лінійних колах при періодичних, але несинусоїдних е.р.с. або струмах, найпростіше досліджувати, якщо е.р.с. або струми розкласти в тригонометричний ряд Эйлера-Фур'є:

,

(12.1)

де при k = 0, А_km = А₀, а φ_k = ψ₀ = 90º.

Перший член ряду А₀ називається постійною складовою або нульовою гармонікою, другий член – основною синусоїдою або першою гармонікою, а всі останні члени вигляду при k > 1 носять назву вищих гармонік.

Тригонометричний ряд після перетворення синуса суми кожної гармоніки можна ще записати так:

(12.2)

де .

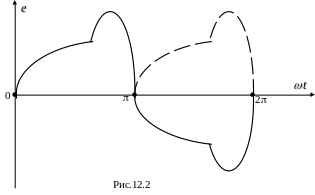
Если несинусоидальная функция соответствует условию:

f(ωt) = –f(ωt + π),

то в этом случае ряд не содержит чётных гармоник и постоянной составляющей. Одна из таких функций изображена на рис.12.2. Она расположена симметрично относительно оси абсцисс.

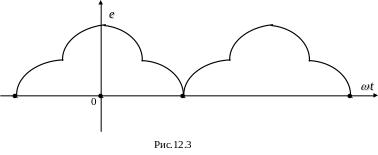
Если несинусоидальная функция соответствует условию:

f(ωt) = f(–ωt),

то ряд не содержит синусов. Одна из таких функций изображена на рис.12.3. Она расположена симметрично относительно оси ординат.

Возможные другие варианты несинусоидальных функций.

Якщо несинусоїдна функція відповідає умові:

f(ωt) = –f(ωt + π),

то в цьому випадку ряд не містить парних гармонік і постійної складової. Одна з таких функцій зображена на рис.12.2. Вона розташована симетрично відносно осі абсцис.

Якщо несинусоїдна функція відповідає умові:

f(ωt) = f(–ωt),

то ряд не містить синусів. Одна з таких функцій зображена на рис.12.3. Вона розташована симетрично відносно осі ординат.

Можливі інші варіанти несинусоїдних функцій.