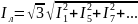30. Действующее значение несинусоидального тока

Несинусоидальный ток складывает­ся из постоянной составляющей и ряда гармоник: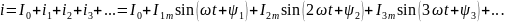

Это соответствует формуле ряда Фурье. А используя закон Джоуля-Ленца для выделения тепла, можно получить

г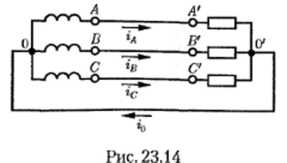 де (Q - теплота, выделяемая за один период Т при несинусоидаль­ном токе, действующее значение которого равно

Преобразуя данные формулы через выделенное тепло, и сокращая постоянные составляющие в этой формуле можно получить: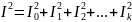

О тсюда следует, что действующее значение несинусоидального тока является средней квадратичной из постоянной составляющей и действующих значений синусоидальных составляющих этого тока:

Аналогичное выражение можно получить и для действующего значения несинусоидального напряжения:

Мощность в электрической цепи при несинусоидальном токе

После сокращения формулы теплового баланса( ) на Т получим уравнение активных мощно стен:

Активная мощность в цепи несинусоидального тока равна сумме активных мощностей, соответствующих постоянной составляю­щей и отдельным гармоникам.

31. Высшие гармоники и трехфазных цепях.

Рассмотрим известные схемы соединения трехфазных систем при несинусоидальных напряжениях. При этом будем полагать, что напряжения не содержат постоянных составляющих и четных гар­моник, т.е. рассматриваются кривые напряжения, симметричные относительно оси абсцисс, которые в практике встречаются наибо­лее часто.

Симметричные составляющие гармоник

Симметричная трехфазная система напряжений, как известно, характеризуется тем, что кривые напряжений во всех фазах по фор­ме одинаковы, но сдвинуты на одну треть периода (2π/3).

Основную гармонику напряжений можно выразить системой трех уравнений: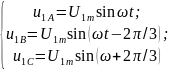

Р ассмотрим сначала гармоники, кратные трем, т.е. положим к = 3n, где n — целое число:

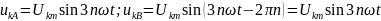
Гармоники, кратные трем, об­разуют симметричную систему нулевой последо­вательности.

На рис. 23.13, а гармоники напряжения, кратные трем, показаны тремя одинаковыми векторами, совпадающими по направлению.

Например, четвертые гармоники фазных напряжений (к—4) вы­ражаются уравнениями

Следовательно, гармоники 1,4,7,10,13 и т.д. образуют симмет­ричную систему прямой последовательности.

Векторы диаграммы нужно представлять вращающими­ся против движения часовой стрелки с угловой скоростью Kw, при этом порядок следования векторов прямой такой за вектором U_А следует вектор Uв а затем Uс.

Гармоники 2, 5, 8, 11, 14 и т.д. образуют симмет­ричную систему обратной последовательности. Порядок следования векторов диаграммы на рис. 23.13, в при вра­щении их против движения часовой стрелки обратный: за вектором U_А следует U_с и далее U_в

Соединение звездой

При соединении обмоток источника звездой (рис. 23.14) линей­ные напряжения равны разностям фазных напряжений двух смеж­ных фаз.

Совпадая по фазе, гармоники фазных напряжений, кратные трем (к = 3; 6; 9;...), при вычитании дадут нуль. Поэтому в линейных напряжениях гармоники, кратные трем, отсутст­вуют.

Таким образом, при симметричной нагрузке в нулевом проводе имеется ток, равный утроенной сумме токов высших гармоник ну­левой последовательности;

2 При отсутствии нулевого провода сумма фазных токов в лю­бом случае равна нулю, поэтому в составе.фазных токов гармоники, кратные трем, должны отсутствовать. Следовательно, фазные на­пряжения на нагрузке не могут содержать гармоник, кратных трем.

Такое смещение нейтрали, связанное с действием гармоник тока, кратных трем, может наблюдаться в электрических сетях напряже­нием 6-35 кВ с изолированной нейтралью.

Соединение треугольником

Обмотки генератора или трансформатора, соединенные тре­угольником образуют замкнутый контур. Результи­рующая ЭДС трех фаз в этом контуре равна нулю, если ЭДС каж­дой фазы не имеет гармоник, кратных трем, так как трехфазная сис­тема ЭДС каждой гармоники является симметричной системой прямой или обратной последовательности.

Вольтметр, включенный последовательно в контур обмоток покажет общее напряжение

В замкнутом треугольнике об­моток источника без нагрузки (внешняя цепь источника ра­зомкнута) результирующая ЭДС гармоник, кратных трем, вызыва­ет ток, который условно назовем внутренним или уравни­тельным (рис. 23.15, б).

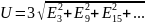
У равнительный ток вызыва­ет в обмотках источника падения напряжения, уравновешивающие ЭДС этих гармоник.

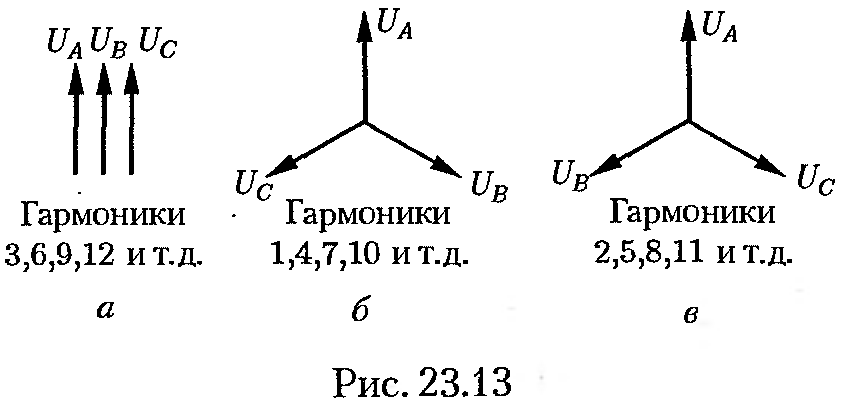Р езультирующая ЭДС гармоник, не кратных трем, является фазным (и линейным) напряжением источника при отсутствии нагрузки:

Таким образом, фазный ток генератора

Линейный ток во внешней цепи