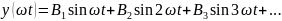28.Несинусоидальные напряжения, токи и их выражения.

1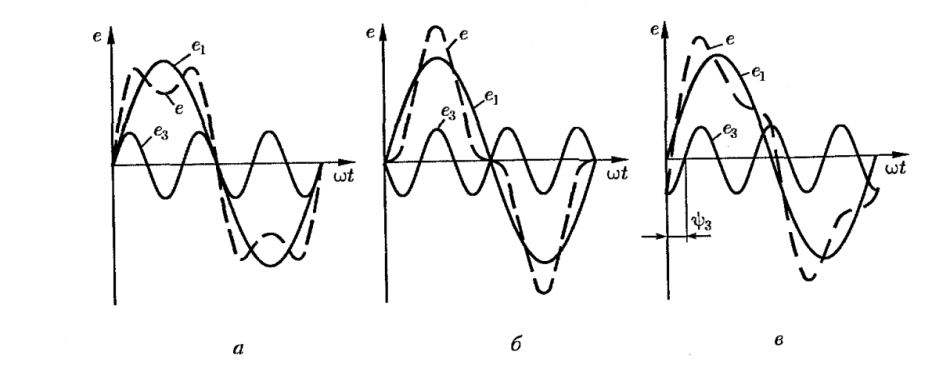 )Несинусоидальные напряжения и токи, причины их возникновения Конструкция генераторов переменного тока не позволяет получить синусоидальную ЭДС. Распределение магнитной индукции по полюсам является несимметричной. Наличие ферромагнитного сердечника приводит также к несинусоидальности. Таким образом, получаем кривые, имеющие несинусоидальную форму.

2)Выражение несинусоидальных токов и напряжений при помощи рядов Фурье. Коэффициенты ряда Фурье. Для того, чтобы определить ЭДС электрической цепи в расчетах используют формулу ряда Фурье, в основе которой лежит определение коэффициентов ряда, при этом участок несинусоидальной ЭДС разбивают на отдельные симметричные составляющие: 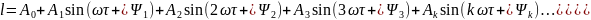В данной формуле ряда Фурье - постоянная составляющая; и тд- амплитуды переменных составляющих, которые называются гармониками. . Используя теорему ряда Фурье можно представить несинусоидальные ЭДС в ряд синусоидальных составляющих. На рисунке выделим соответствующие гармоники. Первая является основной, период которой равен периоду несинусоидальной ЭДС, все другие гармоники называются неосновными, номер которой соответствуют количеству колебаний в периоде несинусоидальных ЭДС. Используя теоремы синусов и косинусов можно выделить только нечетные колебания. Основные гармоники 1,3,5 образуют активные составляющие и выделяют активную мощность, все другие являются гармониками рассеивания и искажают первую гармонику. За исключением первой от всех высших гармоник стараются по возможности избавиться при помощи механических конструкций и различного рода фильтров. Используя правила сложения и вычитания синусоид можно получить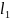: l= + ; l= +sin + sin

29. Симметричные несинусоидальные функции

Периодические функции, с которыми приходится встречаться в электротехнике, чаще всего имеют симметрию. Одни из них сим­метричны относительно оси абсцисс, другие — относительно оси ординат или начала координат.

Функция, симметричная относительно оси абсцисс

Н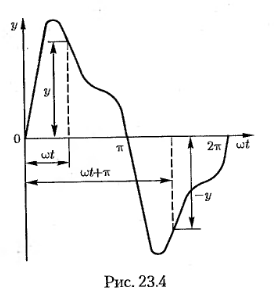 а рис. 23.4 показан график функции, симметричной относи­тельно оси абсцисс. При симметрии относительно оси абсцисс значения функции повторяются с обратным знаком через половину периода, поэтому отрицательная полуволна, сдви­нутая на половину периода, явля­ется зеркальным отображением положительной полуволны.

Такую форму имеет кривая тока в катушке с ферро­магнитным сердечником при си­нусоидальном напряжении.

Таким образом, кривая, симметричная относительно оси абсцисс, выражается тригонометрическим рядом следующего вида:

или

Функция, симметричная относительно оси ординат

Симметрию относительно оси ординат имеют кривые, у которых при изменении знака аргумента величина и знак функции не меня­ются:

Такую симметрию имеет, например, ток в нагрузке схемы однополупериодного выпрямления.

функция, симметричная от­носительно оси ординат, не со­держит синусов:

Функция, симметричная относительно начала координат

Симметрия относительно начала координат (рис. 23.6) соответ­ствует условию

В этом случае при изменении знака аргумента функция меняет знак, не меняя величины. Такая функция не содержит постоянной составляющей и косинусов.

Нетрудно заметить, что в данном случае в обеих половинах пе­риода имеются две равные по величине ординаты с разными знака­ми. Поэтому среднее значение функции за период» или постоянная составляющая, равно нулю. Отсутствуют и несимметричные отно­сительно начала координат косинусоидальные составляющие.

Функция имеет только ряд синусов, обладающих симметрией такого же характера, как и функция в целом: