
- •1.Получение синусоидальной эдс.
- •2.Уравнение и графики синусоидальных величин.
- •3.Действующее и среднее значение переменного тока
- •4.Мощность в цепи переменного тока.
- •5.Цепь с реальной катушкой индуктивности.
- •6.Цепь с реальным конденсатором.
- •7.Последовательное соединение катушки и конденсатора.( 8. Расчет неразветвленных цепей переменного тока.)
- •9. Выражение характеристик электрических цепей комплексными числами.
- •11. Проводимости в комплексной форме.
- •12. Мощность в комплексной форме.
- •13. Основные уравнения электрических цепей в комплексной форме.
- •14. Резонанс напряжений.
- •1 5.Резонанс токов
- •16.Компенсация реактивной мощности.
- •17.Круговые диаграммы
- •18.Построение круговой диаграммы по результатам опытов холостого хода и короткого замыкания.
- •19.Общие сведения о трехфазных системах
- •20.Соединение звездой при симметричной нагрузке
- •21.Соединение треугольником при симметричной нагрузке
- •22. Расчет симметричных трехфазных цепей.
- •28.Несинусоидальные напряжения, токи и их выражения.
- •29. Симметричные несинусоидальные функции
- •30. Действующее значение несинусоидального тока
- •31. Высшие гармоники и трехфазных цепях.
- •32.Токи в цепи с вентилями.
- •33. Эдс, магнитный поток и ток в цепи с нелинейной индуктивностью.
- •34. Полная векторная диаграмма и схемы замещения катушки с ферромагнитным сердечником.
- •35.Общие сведения о переходных процессах.Причины возникновения переходных процессов
22. Расчет симметричных трехфазных цепей.
Цель
расчета состоит в определении токов в
фазах приемника и проводах линии, а
также мощности приемника в целом и в
каждой фазе. Может быть поставлена и
обратная задача.
Соединение
звездой:
1)
Находим сопротивления фаз:

2)
Uф=
Uл/
3)Iф= Iл= Uф/Z
4) cosϕ=R/Z; sinϕ=XL/Z = -Xc/Z;
5) P=3UфIфcosϕ =∑P; Q=3UфIфsinϕ =∑Q; S=3UфIф=∑S
Соединение треугольником:
1) Находим сопротивления фаз:
2) Uф=Uл
3)Iф=
Uф/Z;
Iл= Iф
Iф
4) cosϕ=R/Z; sinϕ=XL/Z = -Xc/Z;
5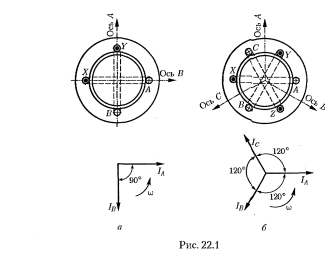 )
P=3UлIлcosϕ
=∑P;
Q=3UлIлsinϕ
=∑Q;
S=3UлIл=∑S
)
P=3UлIлcosϕ
=∑P;
Q=3UлIлsinϕ
=∑Q;
S=3UлIл=∑S
23.Расчет несимметричной трехфазной цепи при соединении источника и приемника звездой. Трехфазная цепь не симметрична, если комплексы сопротивления ее фаз неодинаковы. При соединении звездой трехфазная система представляет собой электрическую цепь с двумя узлами — нейтральными точками N и N̒. Наиболее удобным методом расчета в данном случае является метод узловою напряжения.
1)
Напряжение между нулевыми точками N
и N̒,
или узловое напряжение:
 2)
Напряжение на фазах приемника:
2)
Напряжение на фазах приемника:
3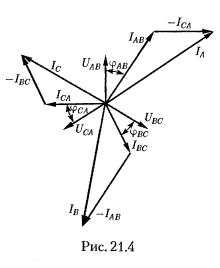
 )
а токи в фазах:
)
а токи в фазах:
 4)
Ток в нулевом проводе :
4)
Ток в нулевом проводе :
 Для
узловой точки N
или N̒
справедливо также уравнение по первому
закону Кирхгофа:
Для
узловой точки N
или N̒
справедливо также уравнение по первому
закону Кирхгофа: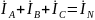 –это
уравнение можно использовать как
расчетное или поверочное.
Роль
нулевого провода
Нулевой
провод является уравнительным. Потенциалы
нейтрали источника и приемника с
помощью этого провода принудительно
уравнены, а поэтому звезда векторов
фазных напряжений приемника точно
совпадает со звездой фазных напряжений
источника.
Четырехпроводная
система применяется в электрических
сетях с напряжением 380/220 В при
электроснабжении от общего источника
силовой (электродвигатели) и осветительной
(электролампы) нагрузки. При несимметричной
нагрузке обрыв нулевого провода вызывает
значительное изменение токов и фазных
напряжений, что в большинстве случаев
недопустимо. Поэтому в нулевой провод
предохранители не устанавливаются.
Определение
мощности
При
несимметричной нагрузке нужно определить
мощность каждой фазы. Например, для
фазы А:
–это
уравнение можно использовать как
расчетное или поверочное.
Роль
нулевого провода
Нулевой
провод является уравнительным. Потенциалы
нейтрали источника и приемника с
помощью этого провода принудительно
уравнены, а поэтому звезда векторов
фазных напряжений приемника точно
совпадает со звездой фазных напряжений
источника.
Четырехпроводная
система применяется в электрических
сетях с напряжением 380/220 В при
электроснабжении от общего источника
силовой (электродвигатели) и осветительной
(электролампы) нагрузки. При несимметричной
нагрузке обрыв нулевого провода вызывает
значительное изменение токов и фазных
напряжений, что в большинстве случаев
недопустимо. Поэтому в нулевой провод
предохранители не устанавливаются.
Определение
мощности
При
несимметричной нагрузке нужно определить
мощность каждой фазы. Например, для
фазы А: Аналогично
определяются мощности других фаз.
Активная
мощность всей трехфазной цепи равна
сумме мощностей фаз:
Аналогично
определяются мощности других фаз.
Активная
мощность всей трехфазной цепи равна
сумме мощностей фаз:

Реактивная
мощность цепи равна алгебраич. сумме
реактивных мощностей фаз:
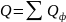
24.Расчет
несимметричной трехфазной цепи при
соединении Треугольником.
Трехфазная цепь при соединении приемника
треугольником и любой схеме соединения
фаз источника имеет разветвленную
многоконтурную схему. Расчет такой
цепи выполняется одним из известных
методов с учетом состава ее элементов
и схемы соединения.
Если трехфазная
система напряжений, приложенных к
приемнику, известна, то фазные токи в
несимметричном приемнике определяются
отдельно по формулам:
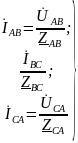 где
где
 -
полные сопротивления фаз.
-
полные сопротивления фаз.
Линейные токи можно определить графически(рисунок 21.4)
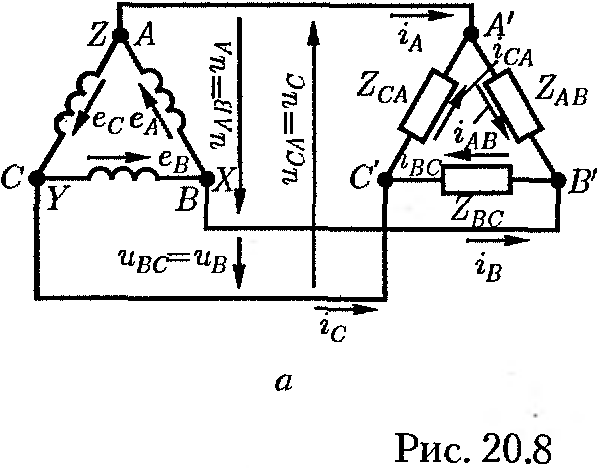 Мощность
в несимметричной трехфазной цепи при
соединении треугольником определяют
по тем же формулам, что и при соединении
звездой:
Мощность
в несимметричной трехфазной цепи при
соединении треугольником определяют
по тем же формулам, что и при соединении
звездой:
 25.
Симметричные составляющие несимметричной
трехфазной системы
Несимметричную трехфазную систему
токов ( напряжений или др синусоидальных
велечин) можно представить в виде трех
симметричных систем.
Разложение
несимметричной системы векторов на
симметричные составляющие применяются
для расчета и анализа несимметричных
режимов в трехфазных цепях.
Комплексы
симметричных составляющих
Первая
система имеет прямую последовательность
фаз (
25.
Симметричные составляющие несимметричной
трехфазной системы
Несимметричную трехфазную систему
токов ( напряжений или др синусоидальных
велечин) можно представить в виде трех
симметричных систем.
Разложение
несимметричной системы векторов на
симметричные составляющие применяются
для расчета и анализа несимметричных
режимов в трехфазных цепях.
Комплексы
симметричных составляющих
Первая
система имеет прямую последовательность
фаз (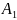 →
→ →
→ ,
рис 21.9, а), вторая- обратную(
,
рис 21.9, а), вторая- обратную( →
→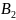 →
→ ,
рис 21.9 б). Третья система, называется
системой нулевой последовательности,
состоит из трех равных велечин,
совпадающих по фазе(
,
рис 21.9 б). Третья система, называется
системой нулевой последовательности,
состоит из трех равных велечин,
совпадающих по фазе( ,
,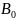 ,
, ,
рис 21.9, в )
Система величин:
прямой
последовательности
,
рис 21.9, в )
Система величин:
прямой
последовательности

Обратной
последовательности: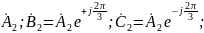 Нулевой
последовательности:
Нулевой
последовательности: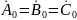
У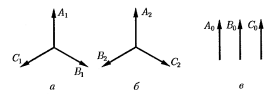 множение
на
множение
на
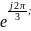 означает поворот вектора на 120 градусов
против движения часовой стрелки.
Обозначив
через
означает поворот вектора на 120 градусов
против движения часовой стрелки.
Обозначив
через
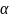 и будем называть это выражение поворотным
множителем.
26.
Получение вращающегося магнитного
поля
Вращающееся
магнитное поле можно получить с помощью
неподвижной системы обмоток, если в
них имеются синусоидальние токи, не
совпадающие по фазе. На рис. 22.1 схематично
показаны две такие системы простейших
обмоток: двухфазная (а) и трехфазная
(б), имеющие по одной катушке на фазу.
Оси катушек двухфазной системы взаимно
перпендикулярны, оси катушек трехфазной
системы пересекаются под углом 120° друг
к другу. Синусоидальные токи в
катушках имеют одинаковые амплитуды
и частоту, но по фазе сдвинуты
относительно друг друга в первом случае
на 90°, а во втором — на 120°.
и будем называть это выражение поворотным
множителем.
26.
Получение вращающегося магнитного
поля
Вращающееся
магнитное поле можно получить с помощью
неподвижной системы обмоток, если в
них имеются синусоидальние токи, не
совпадающие по фазе. На рис. 22.1 схематично
показаны две такие системы простейших
обмоток: двухфазная (а) и трехфазная
(б), имеющие по одной катушке на фазу.
Оси катушек двухфазной системы взаимно
перпендикулярны, оси катушек трехфазной
системы пересекаются под углом 120° друг
к другу. Синусоидальные токи в
катушках имеют одинаковые амплитуды
и частоту, но по фазе сдвинуты
относительно друг друга в первом случае
на 90°, а во втором — на 120°.
Стороны катушек, где начала витков, обозначены А, В, С. Противоположные стороны, где концы витков X, У, Z, отстоят от соответствующих начал по окружности статора на 180°.
Условно-положительное направление токов в обмотках отмечено крестиками в начале витков и точками в конце. Этим условно-положительным направлениям токов по правилу буравчика соответствуют условно-положительные направления осей магнитных потоков, совпадающих с осями одноименных катушек. Магнитное поле такой системы обмоток с токами образуется наложением полей отдельных фаз.
2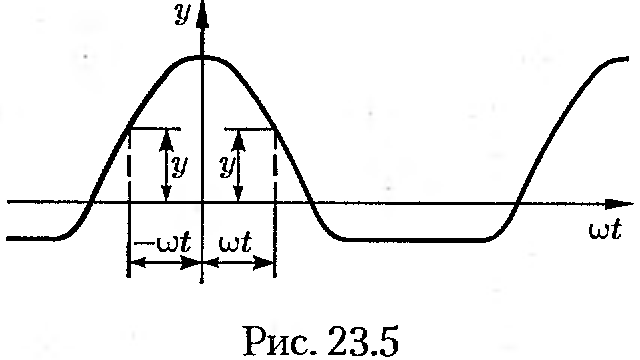 7.
Пульсирующее магнитное поле
При переменном токе в катушке i=
Iт
sin
7.
Пульсирующее магнитное поле
При переменном токе в катушке i=
Iт
sin
 в любой момент времени пространственное
распределение магнитной индукции
остается синусоидальным. Но в каждой
точке воздушного зазора величина
ее изменяется с течением времени по
тому же закону, по какому изменяется
ток.
в любой момент времени пространственное
распределение магнитной индукции
остается синусоидальным. Но в каждой
точке воздушного зазора величина
ее изменяется с течением времени по
тому же закону, по какому изменяется
ток.
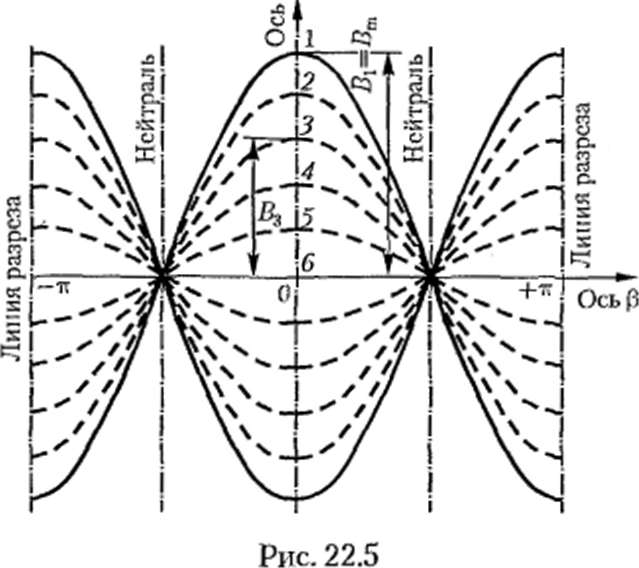
Магнитное поле в этом случае «пульсирует», поэтому оно и называется пульсирующим. В воздушном зазоре образуется стоячая волна магнитной индукции.
На рис. 22.5 показано распределение магнитной индукции в различные моменты времени (кривые 1…6).
 Уравнение
магнитной индукции пульсирующего поля
легко получить, подставив в уравнение
B=Bmcos
Уравнение
магнитной индукции пульсирующего поля
легко получить, подставив в уравнение
B=Bmcos выражение переменного тока
выражение переменного тока
B= Вт sin cos
где
Вт
— магнитная индукция на оси А
при токе в обмотке
i= Iт (кривая
1 на рис. 22.5). При том же токе Im
в обмотке в пункте, стоящем от оси
А
по окружности на угол
=
 /3,
наибольшая величина магнитной индукции
равна
Втcos
/3=
Вт
/2. При
=
/2
магнитная индукция равна нулю при любом
токе катушке.
/3,
наибольшая величина магнитной индукции
равна
Втcos
/3=
Вт
/2. При
=
/2
магнитная индукция равна нулю при любом
токе катушке.
