1 5.Резонанс токов

Так же как и резонанс напряжений, резонанс токов возникает, когда частота источника энергии равна резонансной частоте , а .

Режим электрической цепи при параллельном соединении участков с индуктивностью и ем­костью, характеризующийся ра­венством индуктивной и емкостной проводимостей, называют резонансом токов.

Сначала рассмотрим этот ре­жим для схемы идеализирован­ной цепи (рис. а). В этой схеме параллельно резистору R включены идеальные катушки L и конденсатор С, потери энергии в которых не учитываются.

Реактивные проводимости за­висят от частоты вынужденных колебаний. Для рассматривае­мой схемы:

активная проводимость G=1/R

Реактивные проводимости ;

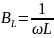При резонансе токов ; ;

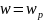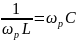
Отсюда определяют резонансную частоту

Выражение для резонансной частоты в данном случае такое же, какое было получено при рассмотрении резонанса напряжений и для частоты собственных колебаний в контуре без потерь.

Резонанс токов, так же как и резонанс напряжений, можно полу­чить изменением параметров L и С или изменением частоты источ­ника энергии.

16.Компенсация реактивной мощности.

Реактивную мощность установок, потребляющих электрическую энергию, надо по возможности сокращать. В тех случаях, когда естественные меры не могут обеспечить оптимальной величины реактивной мощности установки, принимают искусственные меры для ее компенсации.

Одной из таких мер является включение параллельно к прием­никам батареи конденсаторов.

Для определения мощности и емкости батареи конденсаторов должны быть известны: напряжение сети U, реактивная мощность установки до ( Q1) и после ( Q2) компенсации.

Можно установить батарею конденсаторов мощностью Qc= Qv тогда Q2 = 0. Полная компенсация реактивной мощности освобож­дает сеть от реактивного тока.

О днако технико-экономические расчеты показывают, что пол­ная компенсация в большинстве случаев не является оптимальным решением вопроса, так как компенсационное устройство оказывает­ся более сложным и дорогим, чем при некоторой оптимальной вели­чине реактивной мощности Q2, которую определяют на основе тех­нико-экономического сопоставления вариантов¹.

Мощность батареи конденсаторов: Qc= Q1- Q2 ; емкость:

До включения конденсаторов ток в подводящих проводах Iд отстает по фазе от напряжения на угол ϕ1. После включения батарей реактивная составляющая I1р то­ка двигателя частично компенсируется емкостным током Ic, в свя­зи с чем ток в подводящих проводах уменьшается до I, а угол сдвига фаз — до ϕ2 (в обменном энергетическом процессе между генерато­ром и приемником участвует меньшее количество электромагнит­ной энергии).

17.Круговые диаграммы

Для построения окружности, которую называют круговой диаграммой токов, нужно определить ток короткого замыкания Iк, отложить на чертеже в определенном масштабе МI отрезок ОА, соответствующий этому току, и построить на нем, как на диаметре, полуокружность. Ток короткого замыкания устанавливается в цепи

при R = 0, поэтому является чисто индуктивным, отстает от напряжения на 90.

Исходя из этого, определяют направление вектора напряжения. Для выяснения зависимости тока и других величин от активного сопротивления нужно выполнить дополнительные построения в некотором масштабе MR по направлению вектора тока

отложить индуктивное сопротивление X,. Можно, в частности, сопротивление XL выразить тем же отрезком ОА; тогда масштаб сопротивлений MR не будет произвольным:

Из точки А в этом случае проводят прямую AR, перпендикулярную вектору Iк. На этой прямой от точки А в том же масштабе Мк откладывают величины активного опротивления R. Отложив сопротивление R отрезком А В и проведя прямую ОВ, получим треугольник

сопротивлений, гипотенуза которого ОВ выражает полное сопротивление цепи Z.