
- •1.Получение синусоидальной эдс.
- •2.Уравнение и графики синусоидальных величин.
- •3.Действующее и среднее значение переменного тока
- •4.Мощность в цепи переменного тока.
- •5.Цепь с реальной катушкой индуктивности.
- •6.Цепь с реальным конденсатором.
- •7.Последовательное соединение катушки и конденсатора.( 8. Расчет неразветвленных цепей переменного тока.)
- •9. Выражение характеристик электрических цепей комплексными числами.
- •11. Проводимости в комплексной форме.
- •12. Мощность в комплексной форме.
- •13. Основные уравнения электрических цепей в комплексной форме.
- •14. Резонанс напряжений.
- •1 5.Резонанс токов
- •16.Компенсация реактивной мощности.
- •17.Круговые диаграммы
- •18.Построение круговой диаграммы по результатам опытов холостого хода и короткого замыкания.
- •19.Общие сведения о трехфазных системах
- •20.Соединение звездой при симметричной нагрузке
- •21.Соединение треугольником при симметричной нагрузке
- •22. Расчет симметричных трехфазных цепей.
- •28.Несинусоидальные напряжения, токи и их выражения.
- •29. Симметричные несинусоидальные функции
- •30. Действующее значение несинусоидального тока
- •31. Высшие гармоники и трехфазных цепях.
- •32.Токи в цепи с вентилями.
- •33. Эдс, магнитный поток и ток в цепи с нелинейной индуктивностью.
- •34. Полная векторная диаграмма и схемы замещения катушки с ферромагнитным сердечником.
- •35.Общие сведения о переходных процессах.Причины возникновения переходных процессов
11. Проводимости в комплексной форме.
Выражения проводимостей ветвей в комплексной форме можно получить, представив каждый элемент (катушку и конденсатор) схемой параллельного соединения активной и реактивной проводимостей (см. рис.):
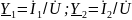
Для первой ветви (катушки)
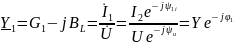
где
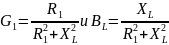 – активная и индуктивная проводимости.
– активная и индуктивная проводимости.
Для второй ветви (конденсатора)
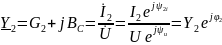
где
 – активная и емкостная проводимости.
– активная и емкостная проводимости.
Результаты этих преобразований показывают, что полная проводимость ветви электрической цепи в комплексной форме выражается комплексным числом, действительная часть которого равна активной проводимости, а мнимая часть равна реактивной проводимости этой ветви, причем индуктивная проводимость отрицательна, а емкостная — положительна.
12. Мощность в комплексной форме.

В алгебраической форме
Рис.
15.4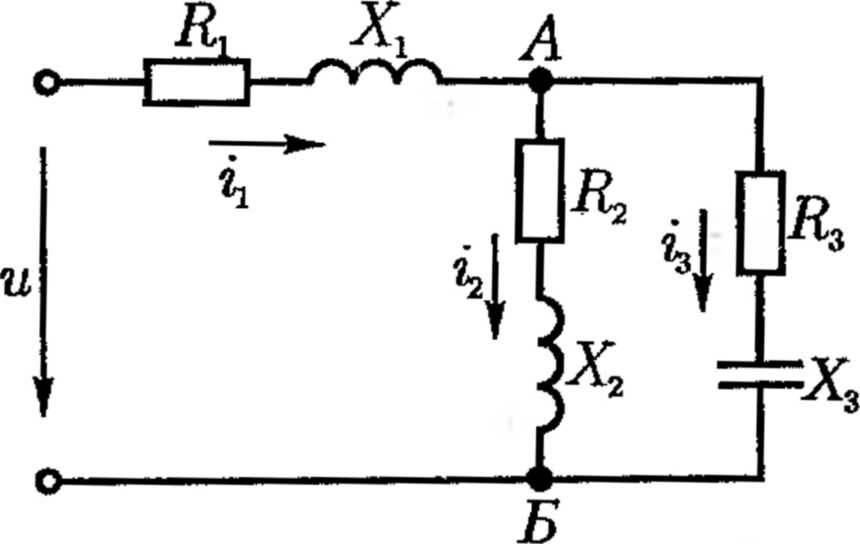
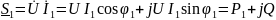
Действительная часть полученного комплекса выражает активную мощность, а мнимая (без множителя j) — реактивную мощность первой ветви.
Для ветви с активным сопротивлением и емкостью
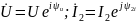

В алгебраической форме
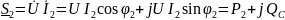
Реактивная мощность в цепи с емкостью имеет отрицательный знак в отличие от положительного знака реактивной мощности в цепи с индуктивностью. Модуль комплекса мощности в той и другой ветви равен полной мощности:
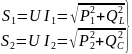
13. Основные уравнения электрических цепей в комплексной форме.
Законы Кирхгофа
Согласно
первому закону Кирхгофа, алгебраическая
сумма комплексов токов в электрическом
узле равна нулю:

Согласно
второму закону Кирхгофа, в
контуре электрической цепи алгебраическая
сумма комплексов в ЭДС источников равна
алгебраической сумме комплексов падений
напряжений:
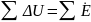
Преобразование схем

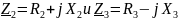

Ток
в неразветвленной части цепи
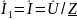
Напряжения
на участках цепи

Токи
в параллельных ветвях

Метод узлового напряжения
С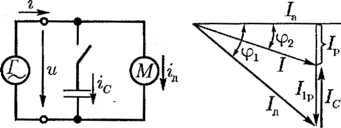 хему
с двумя узлами можно рассчитать,
определив узловое напряжение по формуле:
хему
с двумя узлами можно рассчитать,
определив узловое напряжение по формуле:
 .
В числителе ее записана алгебраическая
сумма произведений комплексов ЭДС и
проводимостей всех ветвей, а в знаменателе
— сумма комплексов проводимостей
ветвей.
.
В числителе ее записана алгебраическая
сумма произведений комплексов ЭДС и
проводимостей всех ветвей, а в знаменателе
— сумма комплексов проводимостей
ветвей.
Комплекс
тока определяют по формуле

14. Резонанс напряжений.
П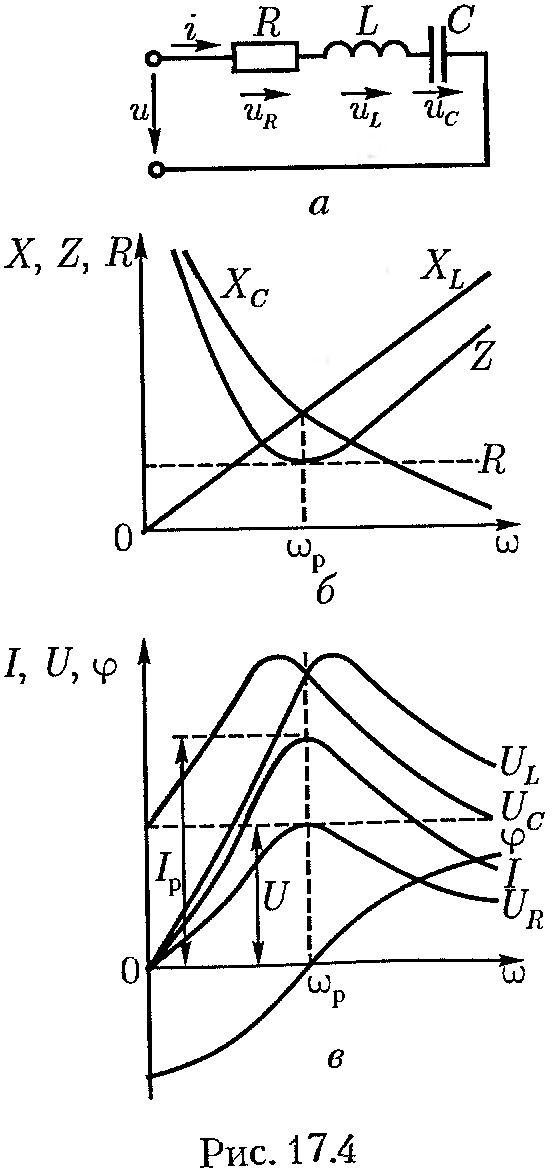
 ри
рассмотрении различных режимов
электрических цепей был отмечен случай
равенства реактивных сопротивлений
ри
рассмотрении различных режимов
электрических цепей был отмечен случай
равенства реактивных сопротивлений
 при последовательном соединении
элементов, содержащих индуктивность
и емкость.
при последовательном соединении
элементов, содержащих индуктивность
и емкость.
В этом случае электрическая цепь находится в режиме резонанса напряжений, который характеризуется тем, что реактивная мощность цепи равна нулю, ток и напряжение совпадают по фазе.
Условие возникновения резонанса
Резонанс
напряжений возникает при определенной
для данной цепи частоте источника
энергии (частоте вынужденных колебаний),
которую называют резонансной
частотой
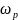 .
.
При резонансной частоте, как будет показано далее, .
Режим электрической цепи при последовательном соединении участков с индуктивностью и емкостью, характеризующийся равенством индуктивного и емкостного сопротивлений, называют резонансом напряжений.
Резонанс
напряжений рассмотрим сначала на схеме
идеализированной цепи (рис. 17.4, а), в
которой последовательно с резистором
 включены идеальные (без потерь) катушка
включены идеальные (без потерь) катушка
 и конденсатор
и конденсатор
 .
.
Реактивные
сопротивления
и
(рис. 17.4, б) зависят от частоты вынужденных
колебаний
 :
:
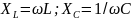
Приравнивая
реактивные сопротивления и учитывая,
что
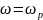 получим
получим

Отсюда
резонансная частота

В
радиотехнике качество резонансного
контура считается тем выше, чем больше
отношение
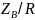 ,
называемое добротностью
контурa
,
называемое добротностью
контурa
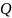 :
:

Чем меньше мощность потерь энергии в контуре (этому соответствует меньшее значение ), тем больше добротность контура.
Большему
значению добротности соответствуют
больший ток
 при резонансе и более острая резонансная
кривая.
при резонансе и более острая резонансная
кривая.
На
рис. 17.5 показаны две резонансные кривые
тока, построенные в относительных
единицах при двух значениях добротности.
По горизонтальной оси отложены отношения
изменяющейся частоты источника энергии
к резонансной частоте
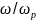 ,
а по вертикальной — отношения тока при
данной частоте к току при резонансной
частоте
,
а по вертикальной — отношения тока при
данной частоте к току при резонансной
частоте
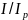 .
.
