1.Получение синусоидальной эдс.

Н а основании закона эл. магн. индукции 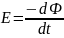, если проводник расположить в магн. поле и придать ему вращательное движение, то в этом проводнике наведётся ЭДС, велечина которой определяется , следовательно используя тригонометрические выражения sinα или cosα данную ЭДС можно представить как sin-идальную величину с периодом изменения Т =2π, а период взятый с опр. временем t и действующий n-раз можно получить мгновенную характеристику в заданных пределах.

2.Уравнение и графики синусоидальных величин.

Анализ электрических цепей переменного тока невозможно про­водить без выражения ЭДС токов, напряжений их уравнениями. Для наглядности применяются графики этих величин в прямо­угольной системе координат.

На рис положение витков соответствует началу отсче­та времени (t = 0) и определяется для каждого из них углом, отсчи­танным от нейтрали до плоскости витка: для первого витка этот угол Ψ_а = 0, для второго — Ψ_в< 0 и третьего Ψс > 0.При вращении ротора ЭДС бу­дет наводиться во всех витках, но уравнения ЭДС не будут одина­ковыми. Действительно, при t = О ЭДС в витках

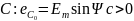
Эта зависимость ЭДС от начального положения витка учитыва­ется введением в уравнение начального угла.

С учетом начального угла ЭДС витка С выражается уравнением

И т.д. Таким образом, в общем виде уравнение ЭДС должно быть запи­сано так:

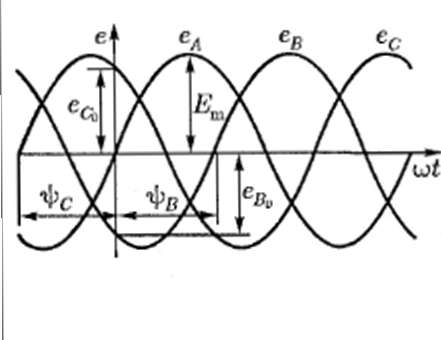Из этого уравнения можно определить величину ЭДС в любой момент при произвольном начальном положении витка.

3.Действующее и среднее значение переменного тока

Действующе значение переменного тока

Действующе значение переменного тока I численно равно вели­чине постоянного тока, который в одном и том же элементе цепи за время периода Т выделяет столько же теплоты, сколько при тех же условиях выделяет переменный ток.

Действующее значение синусоидального тока меньше его амплитуды в раза.

Действующие значения тока измеряется электроиз­мерительными приборами. Номинальные токи и напряжения элек­тротехнических устройств выражаются действующими значениями, для которых в дальнейшем будем строить векторные диаграммы.

Отношение амплитуды к действующему значению называется коэффициент амплитуды Кл. Для синусоидальной функции этот коэффициент равен ; если кривая тока или напряже­ния имеет более острую форму, чем синусоида, то Кл > , в против­ном случае Кл < , (при прямоугольной форме Кл = 1).

Среднее значение переменного тока

Средним значением переменного тока (ЭДС, напряжения) назы­вается среднее арифметическое из всех мгновенных величин за полупериод.

Среднее значение равно высоте прямоугольника с основанием π(в угловой мере), площадь которого равна площади S, ограниченной положительной полуволной тока и осью абсцисс

Для определения площади S нужно сложить в пределах полупе­риода элементарные площади dS, одна из которых на рисунке пока­зана при некотором угле ωt и мгновенном значении тока i.

dS = dl sinωt

Такие же рассуждения можно привести для последующих и пре­дыдущих изменений угла и ωt на dωt. Следовательно, сумму S элемен­тарных площадей dS, взятую за полупериод можно приравнять проекции полуокружности на ее диаметр: S = 2 Im.

Таким образом

Среднее значение синусоидального тока

Iср = 2 Im/π

Отношение действующею значения к среднему называется ко­эффициентом формы кривой Кф.

Кф = I/ Iср

Для синусоиды

Кф