6.Гидромеханические процессы и аппараты.Класиф.Неоднор систем и методов их разделения.

Простые в-ва назыв. фазами или компонентами(ж.ф, тв.ф), а сложные смеси – системы из нескольких фаз или компонентов.В зависим. от состава сложн. системы дел.: -гомогенные(имеющие во всех своих частях одинак. св-ва: вязкость, плотн.,;это- р-ры щелочей, кислот, газов смеси.); -гетерогенные(явл. не однородными в своем объеме, сост. из основной дисперсной (сплошной) фазы, и взвешенной. Содерж. сплошн. фазы>50%, на практике 90%.

В зависимости от размера и составл. частиц взвеш. фазы след. классификация неоднор систем: (1)Г-Т (dч<5мкм-дым, аэрозоль; >5мкм – пыль); (2)Г-Ж (<5мкм – туман(аэрозоль); >5мкм – аэрозоль); (3)Ж-Т(суспензия:>100мкм-грубая, 0.1-100мкм-тонкая; коллоидные р-ры <0.1мкм); (4)Ж-Ж(эмульсия); (5)Ж-Г(пена, барбатажный слой); (6)Т-Т(сплав).

Методы раздел. неоднор.ситем в зависим. от движ. силы и состава ситемы: (1) Сила тяжести(если внешн.дисперсная среда Ж-осаждение, Г-осаждение); (2) Инерционная(центробежная) (Ж-центрифугирование, Г-центробежная сепарация); (3) Разность давлений (Ж-фильтрование, Г-фильтрование); (4) Электрич. силы (Ж-разделение электрокосмосом, Г-электрофильтрация); (5) Поверхностные силы (Ж-флотация, Г-мокрая очистка).

Р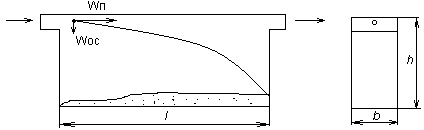 аздел. неоднор. систем в поле сил тяжести. Относятся процессы разделения: суспензий, эмульсий, запыленных газов. Рассм. пример осажд. частиц в проточном отстойном аппарате прямоуг. формы. Если скорость сплошной среды вместе со взвешенными частицами принять постоянной, то время пребывания частиц в камере составит: . Согласно рис. в наиб. неблагоприятном полож. будут нах. частицы в левом верхнем углу, кот осядут только если , , продольную скорость выражаем через объемный расход: , подставим , или , имеем зависимость , F-площадь осаждения. Из этой формулы высота камеры не играет решающей роли, а производительность определяется площадью и скор. осажд.

7.Определение скорости осажд. Частиц, вывод формулы Стокса.

Согласно з-ну Ньютона, сопротивление среды движущемуся в ней тела опред. зависимостью: , -коэф. сопротивления.S-площадь проекции тела на плоскость -ой направлению его движения. Что бы происходило движение частицы в сплошной фазе сумма сил действующих на частицы должна быть силам сопротивления: . В поле сил тяжести, на кажд. элементарную частицу будет действовать сила тяж., за вычетом силы Архимеда и силы сопротивления. G-A=R, , d-диаметр частиц, -плотность материала. . Под действ. этих сил частица в нач. период будет перемещ. с ускорением в этом случ. исп. принцип Даламбера, получим ДУ движ частицы: ; . Установлено, что скор. движения частиц в реальн. среде очень быстро достигает своего предела: , т.е.: . т.е . Имеет место 3 режима движения: ламинарный, переходной, турбулентный. Для ламинарного режима осаждения: , если подставим то получим ф-лу Стокса: , . Она применима для но и .

Для , , . Для турбул. режима .

8.Определение скорости осажд. Или диаметра частиц графическим методом с использованием Ar,Re,Ly.

Л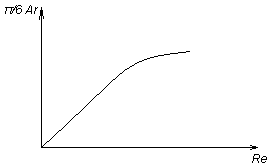 ященко предложил свой метод, в ур-ии он домножил прав. и лев. части на комплекс: , В этом ур-ии , , . В критерий Ar не вх. скорость зато есть диаметр частиц, следовательно по Ar ищем Re а затем скорость.

Иногда нужно опред. не скор. осажд. а min d частиц, кот могут улавливаться в конкр. аппарате. Опред d по скор. – обратная задача. Для таких задач Лященко предложил исп. нов. безразмерный комплекс: .

9.Универс. метод определения скорости осаждения частиц по графику Ly=f(Ar), стесненое осаждение.

О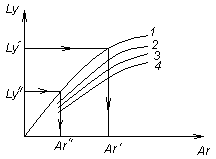 бобщая результаты эксперим. исследований, была предложена универс. зависимость Ly=f(Ar) c пом. кот можно реш. прям. и обр задачи. Прям. задача d-Ar-Ly-Wос, обр. Wос-Ly-Ar-d. Скор. осажд. частиц нешарообр. формы < чем шарообр. Что бы ее опред нужно скор. шарообр. умнож. на поправочн. коэф.- коэф. формы, он всегда <1. Для частиц неправильн. формы Re и Ar расч. по эквивалентному диаметру .

Приведенные закономерности осажд. частиц в поле сил тяж. оказыв. справедлив.для сильно разбавл. суспензий в больш. объеме. В реальности осущ. стесненное осажд. т.е. когда совместно движ. большое кол-во частиц влияющих друг на друга, и скор. осажд ниже чем для одиночн. С гидродинамич т. зрения стесненное осажд. аналогично псевдоожиж., когда скор. движ.=скор. своб. летания частиц. Тогда для всех режимов: 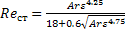. 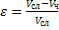- порозность слоя. .