56.Теплопередача через плоскую стенку при постоянных температурах.

Т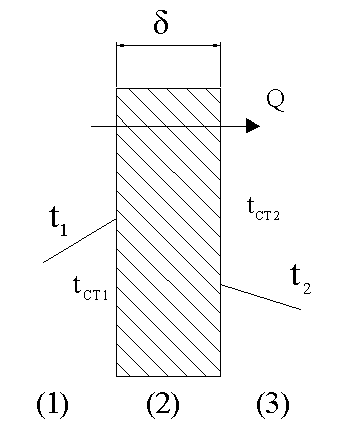 еплопередача-теплообмен между двумя средами разделёнными стенкой или поверхностью контакта. Количество переданной теплоты от одного к другому при стационарном теплообмене определяют по основному уравнению теплопередачи. Вывод которого рассмотрен для случая когда две среды разделены плоской стенкой толщиной с коэффициентом теплопроводности . коэффициент теплоотдачи со стороны горячего теплоносителя, -холодного. Принимаем, что высота и ширина достаточно большие, по сравнению с толщиной, температурное поле принимается однородным. При установившемся процессе кол-во теплоты переносимое в каждой из трёх зон будет выражаться зависимостью:

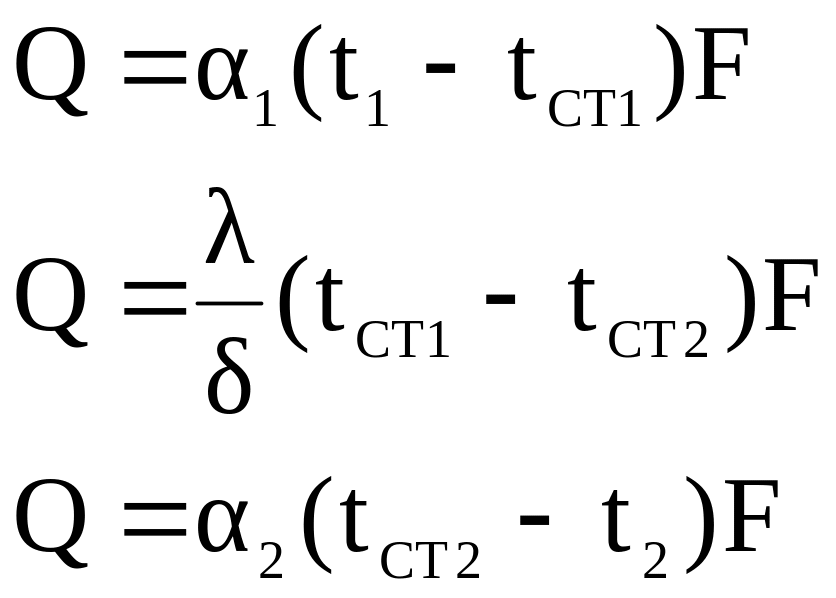из системы находим частные температурные напоры или термические сопротивления на соответствующих участках.

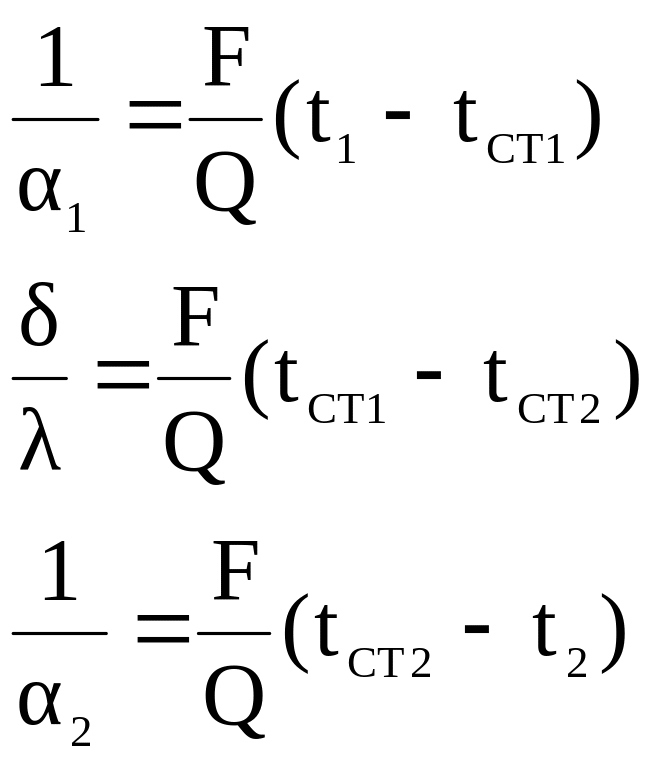общее сопротивление = ;

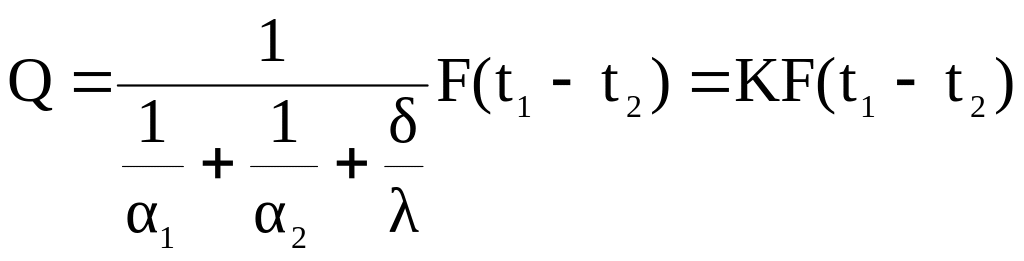, где K=коэффициент теплопередачи, (Вт/м²К). К характеризует скорость теплопереноса от одного теплоносителя к другому через разделяющую их стенку поверхностью 1м² в течении 1с при . Для многослойной стенки (с загрязнениями) , где - сумма термических сопротивлений стенки и возможных загрязнений по обе стороны стенки.

, если пренебречь термическим сопротивлением стенки, то , так как сумма слагаемых больше каждого из них, то , отсюда , то есть К меньше наименьшего из .

57.Уравнение теплопередачи при переменных температурах теплоносителей. Определение средней разности температур. Выбор направления тока жидкости.

Н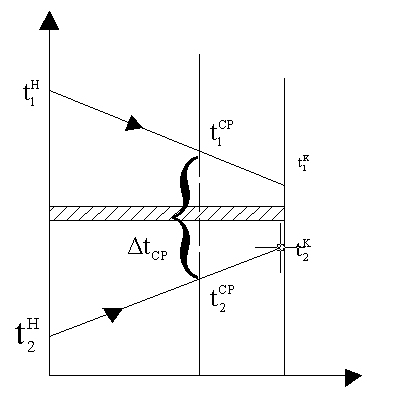 а практике чаще всего теплоносители перемешиваются вдоль стенки теплообменника и их температура непрерывно изменяется при нагревании и охлаждении сред. Следовательно в любой точке изменяется и величина теплового потока Q.Если t обоих сред меняется не очень существенно, то их изменения принимают линейными: ;

Если , то пользуются логарифмической зависимостью:

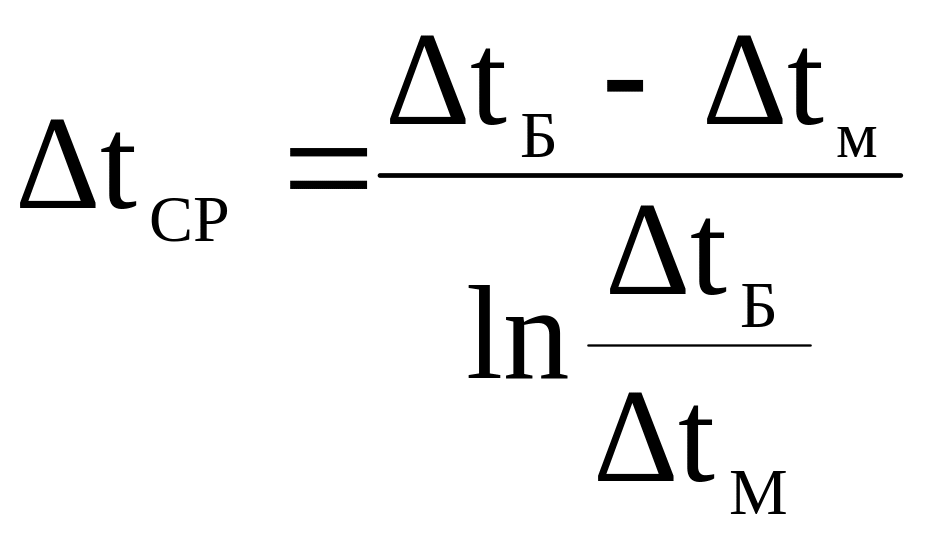при коэффициенте передачи равном константе . При теплообмене теплоносители могут перемещаться относительно друг друга по-разному:

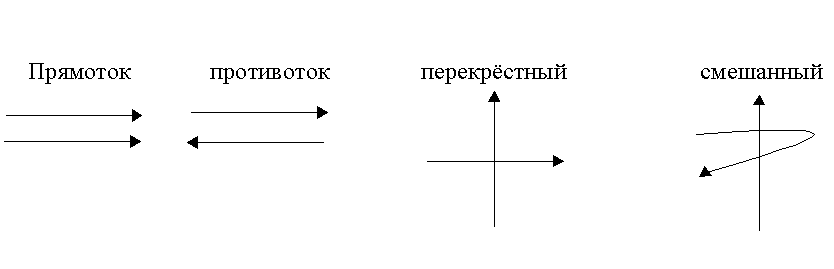
По экспериментальным данным максимальная сила движения при противотоке, min – прямотоке. При проектировании выгоднее предусматривать противоток, так как при большой движущей силе мат.затраты на проведение процесса меньше будут. Для перекрёстного и смешанного значение движущей силы определяют через для противотока с поправочным коэффициентом

58. Сложный теплообмен. Зависимость коэффициента теплопередачи от частных коэффициентов теплоотдачи.

Если теплообмен происходит между твёрдой стенкой и газообразной средой, например воздухом, то тепло передаётся совместно конвекцией и излучением, подобные процессы переноса тепла носят название сложная теплоотдача.

K=коэффициент теплопередачи, (Вт/м²К). К характеризует скорость теплопереноса от одного теплоносителя к другому через разделяющую их стенку поверхностью 1м² в течении 1с при . Для многослойной стенки (с загрязнениями) , где - сумма термических сопротивлений стенки и возможных загрязнений по обе стороны стенки.

, если пренебречь термическим сопротивлением стенки, то , так как сумма слагаемых больше каждого из них, то , отсюда , то есть К меньше наименьшего из .

59 Прямые источники тепла промежуточные теплоносители. Нагревание водяным паром, и парами высококипящих жидкостей, топочными газами и электрическим током

Прямые ист. тепла: 1)дымовые газы,2)электрич.ток. Промеж. теплоносители: 1) вод. пар, 2) минеральные масла, 3) спец. теплоносители: перегретая вода, высококипящие жидкости и их пары, расплавленные неорганич. соли и их смеси и др. Для нагревания может быть использовано тепло отходящих газов и жидкостей высокой температуры. Требования: 1) хорошие тепло-физ. свойства (↑r, ↑c, ↓μ, ↑ρ, ↑λ), 2) термостойкость и термостабильность, 3) неагрессивность, 4) доступность и ↓ стоимость. Вод. пар имеет ↑ теплосодержание по сравнению с другими теплоносителями. При таком нагревании можно точно регулировать tºС нагрева, изменением давления пара. Из-за хорошей теплоотдачи аппараты могут иметь меньшие пов-ти нагрева, чем при нагревании дымовыми газами. Но получить ↑ tºС нагрева сложно, т.к. для этого нужно резко ↑ давление пара, на производстве нагревание водяным паром ведут до температур не > 180ºС. Получают его в котлах рекуператорах, пропускают через турбины, после турбины пар называют мятым. Как правило, он перегрет. Его увлажняют, чтобы он стал насыщ., и используют как теплоноситель. Недостаток: для получения более высоких tºС необходимо давление > 16атм, что ведет к утолщению стенок и подорожанию. Прим. обогрев глухим паром (отдает тепло через стенку) и острым (непосредственно через соприкосновение). Для получения температур >180ºС исп. перегретую воду или пары высококипящих жидкостей, обладающих низкой упругостью. Их нагревают или испаряют при помощи электрического тока или дымовых газов, после чего они отдают тепло нагреваемому веществу через стенку, для этого требуются специфич. нагревательные системы. Топочные газы (исп. при нагревании от 180ºС до 1000ºС) получают сжиганием топлива в топках или печах. При нагреве до 400ºС дымовые газы разбавляют воздухом или инертными газами. Недостатки: ↓коэффициенты теплопередачи(10-60Вт/м²*К), жесткие условия теплообмена приводят к перегреву и высоким температурным напряжениям, необходима чистка теплообменных поверхностей аппаратов. Электричесский ток– широкий диапазон температур нагрева (до1500ºС). Электоронагреватели могут быть прямого действия (нагреваемое тело непосредственно или через трансформатор подключается к цепи) косвенного (тепло выделяется в спец. элементах и передается теплопроводностью и конвекцией. Достоинства: легко организовать разный подвод тепла. Недостатки: требуется спец. электротехнич. оборудование, кол-во подводимого тепла одинаково и может произойти расплавление стенок).

60Типы теплообменных аппаратов .Поверхностные теплообменники. Кожухотрубный, спиральный, пластинчатый…

По принципу действия: 1) поверхностные, 2) смешения, 3) регенеративные. Поверхностные по конструктивному действию бывают: а) типа труба в трубе, б) кожухотрубные, в) спиральные, г) змеевиковые, д) пластинчатые. Теплообменники смешения: е)барботеры, ж) полочные, з) насадочные, и) распыливающие. Регенеративные: к) с движущейся насадкой, л) с неподвижной. Подробнее а): состоит из нескольких элементов расположенных один под другим,внутренние трубы одного элемента соединены с внутренними трубами другого, внешние аналогично. Для удобства их соединяют калачами или коленами. Достоинство: подбором диаметров труб можно обеспечить любую максимально допустимую скорость для веществ, участвующих в теплообмене и т.о. достигнуть ↑ коэфф. теплопередачи. б): для сравнительно больших поверхностей теплообмена. В кожухе приварены трубные решетки, в которых находится пучок труб. Бывают одноходовые и многоходовые (размещают горизонтально). В а) и б) теплоноситель подается в межтрубное пространство.в): пов-ть теплообмена образуется 2-мя свернутыми в спираль металлич. листами. Достоинства: компактность, большие коэфф. теплопередачи, меньшее гидравлич. сопрот. Недостатки: сложная конструкция.г): спирально согнутая труба. Достоинства: хороший коэфф. теплопередачи. Недостатки: ↑ гидравлич. сопрот., в нижней части скапливается конденсат, что приводит к ухудшению теплообмена. Исп. в агрессивных средах.

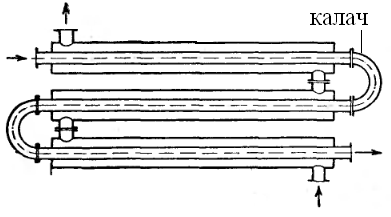
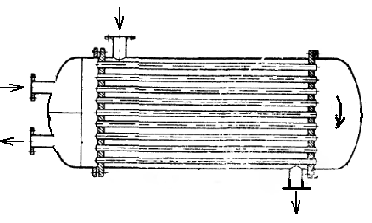
а) б)

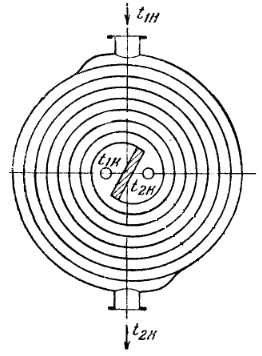
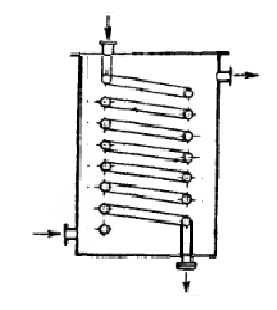
в) г)

д ): на пучки труб надеты пластины для увеличения теплопередачи. Исп. при нагреве воздуха паром д)

61Теплообменники смешения

Теплообменники смешения: барботеры, полочные, насадочные, распыливающие.

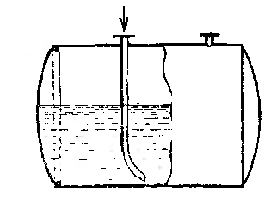
В тех случаях, когда вместе с негревом жидкость нужно перемешивать, исп так называемые барботеры- трубы с небольшими отверстиями.

Полочный барометрический конденсатор:

П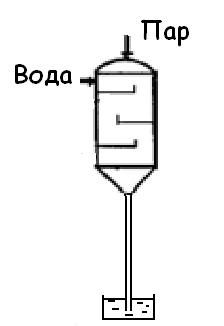 ар и охлаждающая вода смешиваются путем впрыскивания воды в паровое пр-во, пар отдает тепло воде, нагревает ее и конденсируется. Прим. для сжижения паров воды или жидкостей не представляющих ценности. При сжижении пара создается вакуум.

Распыливающий:

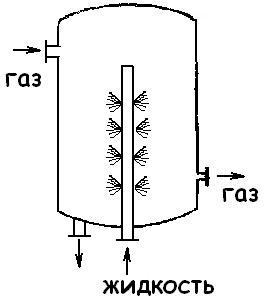
62 Основы процесса выпаривания. tºС кипения растворов

Выпаривание - процесс концентрирования жидких растворов практически нелетучих веществ путем частичного удаления растворителя испарением при кипении. Выпариванию подвергают р-ры тв. веществ (водные растворы щелочей, солей и др.), а также высококипящие жидкости, облад. при tºС выпаривания малым давлением пара, — некоторые минеральные и органические кислоты, многоатомные спирты и др. Выпаривание можно проводить 2 способами: 1) частичное удаление растворителя из всего объема раствора при его tºС кипения (кипение); 2) удаление растворителя с поверхности при tºС меньше tºС кипения раствора (испарение). Кипение –это процесс перехода жидкости в парообразное состояние при такой tºС, когда упругость паров жидкости равна давлению окр. среды. Испарение– это процесс перехода жидкости в парообразное состояние при такой tºС, когда упругость паров жидкости ниже давления окр. среды. В ряде случаев выпаренный р-р подвергают последующей кристаллизации в выпарных аппаратах, спец-но приспособ. для этих целей. Концентрирование р-ров методом выпаривания –распростр-ый технологич. процесс в пром-ти. Т.к. многие вещества, например NaOH, KOH и др., получают в виде разбавленных водных р-ров, а на дальнейшую переработку и транспорт они должны поступать в виде концентрированных продуктов. На выпаривание расходуется большое кол-во тепла. Тепло можно подводить любыми теплоносителями. Но чаще используют насыщ вод. пар, кот. называют греющим, или первичным. Первичным служит либо пар, получаемый из парогенератора, либо отработанный пар. Пар, образующийся при выпаривании кипящего раствора, называется вторичным. Тепло, необходимое для выпаривания раствора, обычно подводится через стенку, отделяющую теплоноситель от раствора. В некоторых производствах концентрирование растворов осуществляют при непосредственном соприкосновении выпариваемого р-ра с топочными газами или другими газообразными теплоносителями.

63 Общая и полезная разность температур при выпарке. Температурная, гидростатическая и гидравлическая депрессия.

Основной движущей силой, опред. интенсивность процесса выпаривания и производительность выпарной установки явл. разность температур между теплоносителем и упариваемым раствором. Разность между температурами греющего и вторичного паров называют общей разностью температур выпарного аппарата: Полезная разность температур- разность между tºС конденсации первичного пара и tºС кипения р-ра Полезная < общей на величину tºС-ных потерь. . Величину наз. температурной депрессией и определяют как повышение tºС кипения раствора по сравнению с tºС кипения чистого растворителя при данном давлении где , - температуры соответственно кипения раствора и чистого растворителя; последняя численно равна температуре вторичного пара при данном давлении. При других давлениях находят с помощью уравнения Тищенко. называют гидростатической депрессией, она характеризует повышение температуры кипения раствора с увеличением давления гидростатического столба жидкости. проявляется в аппаратах с кипением р-ра в кипятильных трубах нагревательной камеры. Тогда за tºС кипения р-ра принимают tºС кипения в средней части кипятильных труб. Тогда где - tºС кипения растворителя при давлении в средней части кипятильных труб, К; - температура вторичного пара при давлении в аппарате , К. Давление в средней части кипятильных труб определяют по выражению где - высота кипятильных труб, м; - плотность парожидкостной смеси в аппарате, кг/м³. - гидравлическая депрессия, потери напора на трение и местное сопротивление.

, где

t₁- tºС над р-ром, - tºС вторичного пара.

64 Технические методы выпаривания. Удельный расход греющего пара при них.

Процессы выпаривания проводят под вакуумом, при повышенном и атмосферном давлениях. Выбор давления связан со свойствами выпариваемого раствора, экономичностью установки и возможностью использования тепла вторичного пара. При выпаривании под вакуумом становится возможным проводить процесс при более низких температурах. Повышается движ. сила процесса, снижается требуемая пов-ть теплообмена и металлоемкость, можно исп. первичный пар более ↓ пар-ров. Выпаривание под атмосферным давлением, а иногда и выпаривание под вакуумом проводят в одиночных выпарных аппаратах (однокорпусных выпарных установках). При выпаривании под атмосферным давлением (проводят в однокорпусных выпарных установках) вторичный пар используется и обычно удаляется в атмосферу. Такой способ выпаривания является наиболее простым, но наименее экономичным. Экономия вторичного пара может быть также достигнута в однокорпусных выпарных установках с тепловым насосом. В таких установках вторичный пар на выходе из аппарата сжимается с помощью теплового насоса (например, термокомпрессора) до давления, соответствующего температуре первичного пара, после чего он вновь возвращается в аппарат. Выпаривание под давлением ↑ атмосферного дает возможность использовать в качестве греющего агента, кроме первичного пара, вторичный пар самой выпарной установки, что снижает расход первичного греющего пара. Удельный расход греющего пара кг/кг d=D/W, где D-расход греющего пара, W- кол-во удаленной влаги. d-экономичность установки, чем она меньше, тем лучше. При однократной выпарке и идеальных условий процесса = 1,04. С учетом потерь d=1.1- 1.2 кг/кг, значит процесс энергоемкий, с целью ↓ энерго затрат нужно применять многократную выпарку или выпарку с тепловым насосом.

65 Материальный и тепловой балансы одно- и многократной выпарки.

Материальный баланс однократной выпарки по общему кол-ву продуктов: по нелетучему продукту: где , – расходы соответственно исходного и упаренного растворов кг/с, и - концентрации растворенного продукта в исходном и упаренном растворе, кг продукта на 1 кг раствора; — кол-во удаленной влаги, кг/с. Тогда , значит и

Тепловой баланс включ в себя приход расход тепла выпарной уст. Приход теплоты= теплоте поступающей с исходным р-ром и греющим агентом. Расход- теплота с уходящим р-ром, теплота с конденсатом греющего пара, теплота фазового перехода растворителя в пар и тепловые потери. Пусть , .

Пусть , =cоnst .

Тогда ,

где , - теплоемкости соответственно исходного и упаренного растворов и растворителя, Дж/кг; ^I_{’ и} ^I’’- энтальпии паров и жидкости соответственно;r- теплота фазового перехода.

Материальный баланс для многократной выпарки по общему кол-ву продуктов отличается тем, что в каждом корпусе удаляется какое-то кол-во влаги: , где n- кол-во корпусов.

Тогда ,значит

Тепловой баланс будет включать уравнения баланса для каждого корпуса при соответствующих температурах и ур-ие мат баланса по выпариваемой воде:

66 Схемы и работа многокорпускных выпарных установок.

Многократное выпаривание проводят в нескольких последовательно соединенных аппаратах, в которых давление поддерживается т. о., чтобы вторичный пар предыдущего корпуса использовать в качестве греющего пара в каждом следующем корпусе. Следствие экономии греющего пара. Общий расход свежего греющего пара на процесс уменьшается почти пропорционально числу корпусов. В зависимости от взаимного направления движения раствора и греющего пара из корпуса в корпус различают прямоточные и противоточные выпарные установки, и установки с параллельной (смешанной) подачей р-ра в аппараты (р-ор параллельно подается во все корпуса, упаренный р-ор удаляется из всех корпусови имеет = конц-ию). Наиб. распростр. прямоточные выпарные установки (рис. 2), в которых греющий пар и выпариваемый р-ор направляют в 1 корпус, затем частично упаренный р-ор самотеком перетекает во 2 корпус, и т. д.; вторичный пар 1 корпуса направляют в качестве греющего пара во 2 корпус, и т.д.

Преимущества: нет насосов; tºС кипения р-ра и давления вторичных паров в каждом последующем корпусе ниже, чем в предыдущем, поэтому раствор в корпуса (кроме 1-го) поступает перегретым. Теплота, которая выд. при охлаждении р-ра до tºС кипения в следующем корпусе, идет на доп. испарение раств-ля из этого же раствора (самоиспарение).

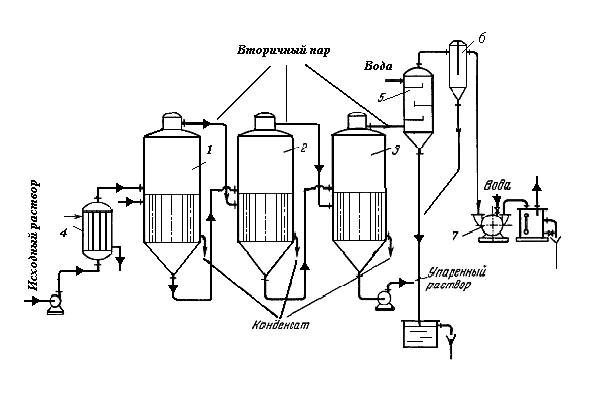
Многокорпусная прямоточная выпарная установка: 1 – 3 – корпуса установки; 4 – подогреватель исходного раствора; 5 – барометрический конденсатор; 6 – ловушка; 7 – вакуум-насос.

Недостатки: понижение температуры кипения и повышение концентрации раствора от 1 корпуса к последнему. Это приводит к ↑ µ р-ра и, след, к ↓ интенсивности теплоотдачи при кипении, ↓ коэффициента теплопередачи и, как следствие, к ↑ общей пов-ти теплопередачи. Если же греющий пар поступает в 1 корпус, а жидкий р-ор — в последний и переходит из последнего корпуса к 1, то установка называется противоточной. Для упаривания растворов с ↑µ и большой в целях ↑ коэфф теплопередачи. Но нужны насосы для перекачки раствора, движ. по направлению ↑ давлений.

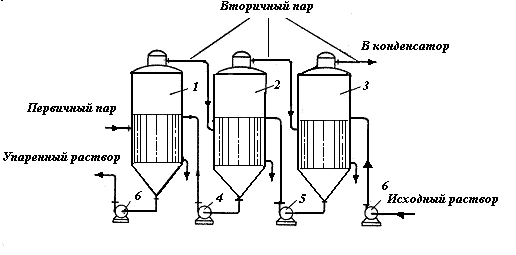
Рис. 3 Многокорпусная противоточная выпарная установка: 1 – 3 – корпуса установки; 4 – 6 – насосы.

Смешанный ток исп для насыщ р-ров, в кот. тв. фаза затрудняет перетекание из корпуса в корпус, и где не нужна ↑ конц-ция

67 Общая и полезная разность температур при многократном выпаривании. Распределение полезной разности температур по корпусам при F₁=F₂=…=F_i

Суммарную полезную разность температур многокорпусной установки находят из уравнения где - общая разность температур многокорпусной установки, равная разности между температурой греющего пара в первом корпусе и температурой вторичного пара, поступающего из последнего корпуса в барометрический конденсатор : , величина характеризует суммарные температурные потери во всех корпусах установки: 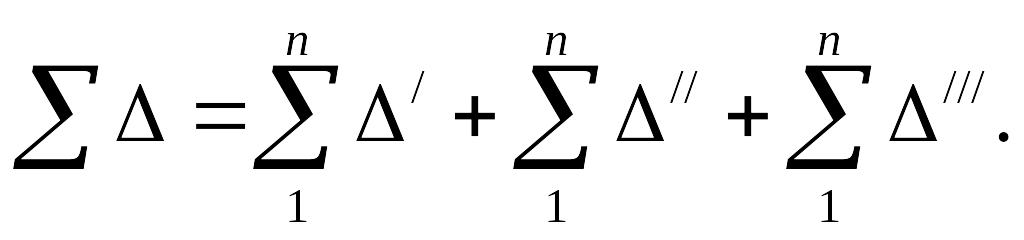температурная (обусл разными tºС кипения р-ра и чистого р-ля при одном давлении) , гидростатической (обусл давлением столба жидкости), гидродинамическая (обусл потерями напора на трение и местное сопротивление) депресси . Для определения полезной разности в каждом корпусе общую полезную разность распределяют между выпарными аппаратами различными способами.

При = пов-тях теплопередачи: полезная разность tºС в корпусе ,суммарная полезная разность температур

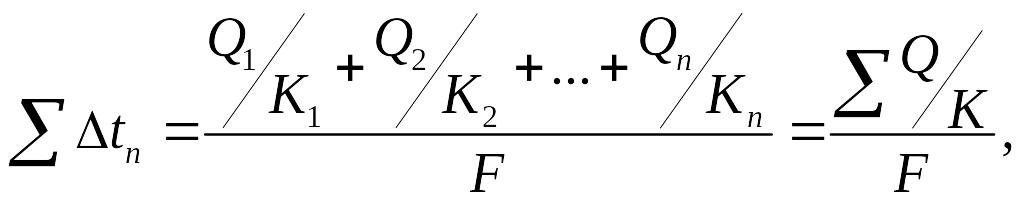
Тогда для произвольного корпуса:

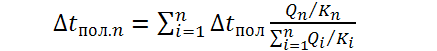Таким образом, при равенстве поверхностей теплопередачи в каждом корпусе суммарная полезная разность температур распределяется пропорционально отношению тепловой нагрузки к коэффициентам теплопередачи в каждом корпусе.

68 Распределение полезной разности температур по корпусам при F₁+ F₂ +…+F_i =F_min

Согласно этому способу распределения (дается без вывода), для любого п-го корпуса:

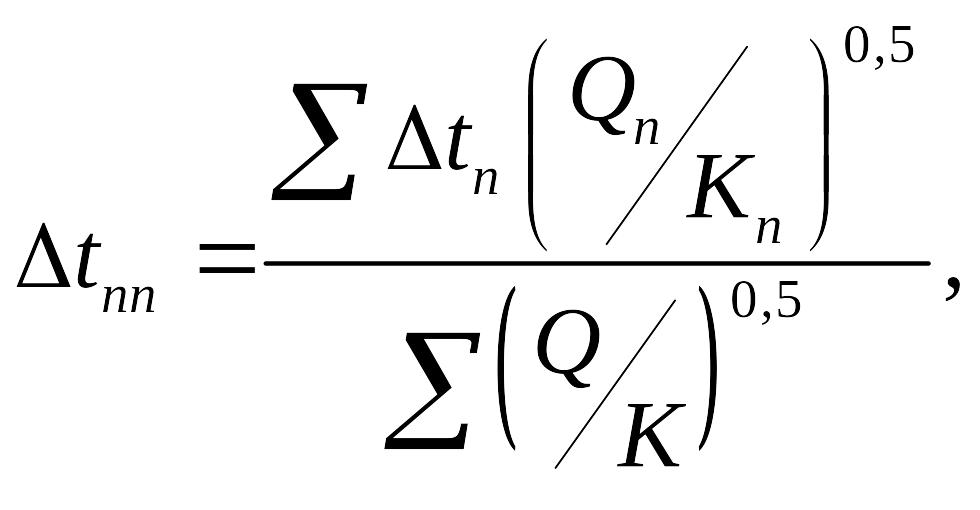
т.е. при минимальной суммарной поверхности теплопередачи многокорпусной установки общая полезная разность температур распределяется пропорционально квадратному корню из отношения тепловой нагрузки к коэффициенту теплопередачи в каждом корпусе. Этот метод предусматривает не равные пов-ти теплообмена, что удорожает изготовление и эксплуатацию, оно выгодно если ВА сост из дорогих мат-ов

80. Движущая сила диффузионного процесса. Возникновение массооб процесса, его направление и предел перехода в-ва из 1-й фазы во 2-ю зависит от степени отклонения с-мыот равновесия. По направлении переноса массы в с-ме можно судить о взаимном положении рабочей и равновесной линий. Рассм 2 случая:

1. рабочая линия располагается выше равновесной. Концентрация Х соот-ет, что рабочая меньше равновесной, а у У наоборот. При этом , - распределенный компопнент переходит из 2-х(абсорбция)

2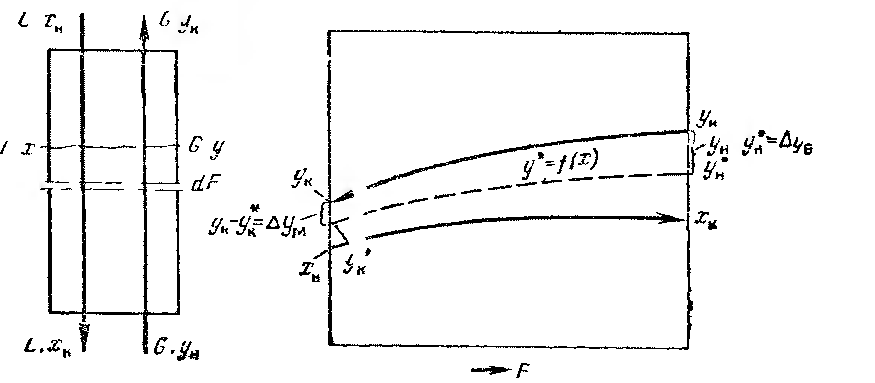 . Рабочая линия распологается ниже равновестной.

При стремлении с-мы к состоянию равновесия распр-й компонент переходит из жидкой фазы в газовую(десорбция) Движущей силой процесса масообмена условно называют разность между рабочей и равнов концентрациями переходного компонента в данной фазе. Знак и указывает на направление переноса массы.

81. Кинетика массообмена. Молекулярная диффузия. 1-й и 2-й з-н Фика. Учение об механизме и скорости переноса распред-го в-ва из 1-й фазы во 2-ю назыв кинетикой массооб-х процессов. При этом перенос в-ва в пределах 1-й фазы к границе раздела фаз и обратно наз-ся массоотдача. Перенос в-ва как внутри так и через пов-ть их контакта наз-ся массапередачей. Согласно исследованиям в неподвижных средах в-во переносится только за счет молекулярной диффузии, а в движущихся фазах за счет молекулярной и конвективной диффузий. 1-й з-н Фика: Молекулярная диффузия в газах и жидкостях происх в рез-те хаот-го движения молекул, не связанного с движением газа или жидкости. При мол диф-зии распред-ое в-во m переносится из зоны с высокой в зону с более низкой концентрациейза счет броуковского движ молекул, до достижения равнофазного равновесия . Рассм молекул перенос на упрощ-ой схеме в с-ме г-ж: в фазе G концен-я распр-го компонента выше равновесной следовательно этот компонент перех из г в ж фазу. Выделим 2 элемент-е площади пов-тью dF. Расст-е между ними . На 1-й концентр распр-го компонента- L1, на 2-й-L2 .L1>L2 тогда grad концентр-ии: кинетика переносав этом случае подчиняется 1-му з-ну Фика, который аналогичен з-ну теплопроводности: кол-во продифундирующего в-ва пропор-на градиенту концентр-ии площади перпендикуларной направлению дифуз-го потока и времени. , D- коэф-т молек-ой диф-зии. Способ выражения концентрации и её размерность опр-ют размерность коэф-та диффузии: Коэф-т молекул-ой диф-ии явл-ся индивидуальным с-вом каждого в-ва.

2-й з-н Фика: согласно 1-му з-ну Фика для каждой входной грани можно записать кол-во кол-во проходящего через неё в-ва за счет молекулярной диф-зии.

; ;

Кол-во в-ва, проходящее через противоположные грани составит:

; ; Или можно записать по-другому изменение в-ва в напрвлении каждой оси составит: ; ; Суммарное кол-во распред-го в-ва в обьеме парал-да =сумме изменений по 3-м направлениям: ; Приравняем обе части и получи 2-й з-н Фика: Данное Ур-е описывает изменение концентрации во времени в элементарном обьеме с изменением концентрации по направлению.

82. конвективный перенос. Ур-е массоотдачи. Для описания механизма массопереноса множество упращенных теор-их моделей. В основу большинства из них положены 1 и те же допущения: 1. Сопр-я массопереносу складыв-ся из сопрот-й каждой из фаз и сопр-я на границе раздела фаз. Допуская, что сопр-е на пов-ти раздела фаз =0 принимаем, что процесс массопереноса в каждой из фаз происходит независимо друг от друга и общее сопр-ие рассматривают как сумму всех сопрот-й. 2. На пов-ти раздела фаз равновесие устан-ся почти мгновенно и равновесная конценирация на пов-ти отличается от соот-ей концентрации в ядре потока. Ур-е массоотдачи : з-н массоотдачи гласит: кол-во в-ва перенесённог от пов-ти раздела фаз в воспринимающую среду пропорц-но разности концентрации у пов-ти фаз и потока восприним-ей фазы, пов-ти фазового контакта и времени: Коэф-т хар-ет такое кол-во в-ва переходит от границы раздела фаз в ядро потока через пл-дь пов-ти 1 в течении 1 сек при разности концентрации=1. При расчете конкретного процесса массопереноса обычно принимают, что коэф-т массоотдачи сохраняет свое значение вдоль пов-ти контакта. Тогда предыдущее Ур-е можно переписать: (G); Входящие в Ур-е разности концентраций выражают собой движущую силу процесса в фазах G и L.

83. ДУ конвективного переноса в-ва. В движущей среде массоперенос осущ-ся как за счет молекул-ой диф-ии так и за счет конвективного переноса. Концентрация распред-го в-ва в элементарном объеме изменяется не только за счет хаот-го движ молекул но и за счет макродвижений турбулентных пульсаций в самой среде, т к среда перемещается в направлении всех 3-х осей х,у,z. Со скоростямиWx,Wy,Wz, то изменение концентрации распред-го в-ва необходимо выражать субстациональной прозв-й учитывающей изменение величины во времени и изменение связанное с перемещением в простр-ве. Если в Ур-ии молекулярной диффузии заменить локальное изменение концентр-ии на полное, то получим ДУ конвективного массопереноса: Данное Ур-е выражает распределение концентрации в-ва движущейся в стационарной среде, при неустан-ся процессе массообмена.

85.Основное Ур-е массопередачи. Выражение движущей силы процессов массопередачи и её осреднение. Всоот-ии с общими кинет-ми законами химико-технолог-х прочесов основной з-н массопередачи можно сфор-ть следующим образом. Скорость процесса массопередачи проп-на движущей силе и обратно проп-на сопротивлению. R- сопротивление процессу массопереноса. Если вместо R взять обратную величину, хар-ю скорость процесса 1\R=K то предыдущее Ур-е примет вид: или Отношение кол-ва распред-го в-ва между фазами к 1 времени для всей пов-ти контакта фаз Ур-е массопередачи примет вид: Согласно основному Ур-ю массопередачи кол-во в-ва М переходящее из фазы в фазу за 1 времени проп-но пов-ти контакта фаз и движущей силе процесса. Коэф-т К выражает собой кол-во в-ва переходящее из 1-й фазы во 2-ю за 1 времени через 1 пов-ти контакта фаз при движущей силе =1: Движ-я сила процесса может быть выражена в любых единицах.

86. связь между коэф-ми массопередачи и массоотдачи. Зав-ть К от установим рассматривая массоперенос распр-го в-ва из фазы G в фазу L на упрощенной модели. Рассмотрим случай, когда равновесная линия прямая т е описывается Ур-ем , m- тангес угла наклона линии равновесия к горизонтали. За 1 времени из фазы G к выделенному элементу пов-ти dF переносится кол-во в-ва равное: за это время от элемент-й пов-ти dF в фазу L переносится кол-во в-ва: тогда для всей пов-ти контакта фаз можно записать: ; При линейной зав-ти между равновесными концентрациями распред-го в-ва в фазах: либо по аналогии , где - концентрация распредел-го в-ва в фазе G равновесна с конц-й в фазе L. Из последних 2-х Ур-й выразим концентрацию в фазе L через конц-ю в фазе G: ; Подставим в Ур-е массотдачи: Выразив движущие силы по фазам: ; сложив левые и правые части Ур-я получим движ-ую силу процесса в целом , Отсюда получаем зав-ти между коэф-ми массоотдачи и массопередачи: ;

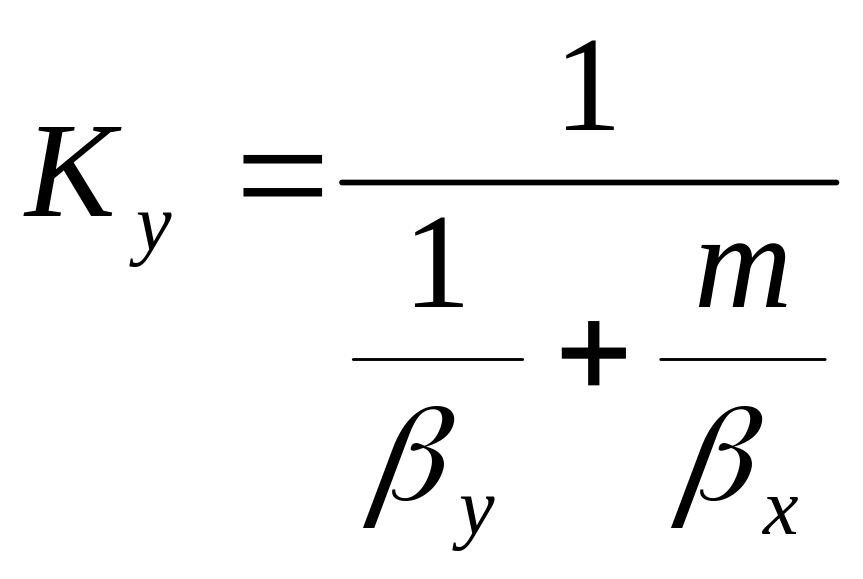- общее сопротивление массопереносу, - диф-е сопр-е газовой фазы, - диф-е сопр-е жидкой фазы, т е по правтлу адитивности общее диф-е сопр-е массопереноса = сумме диф-ых сопр-й газовой и жидкой фаз. При выражении коэф-та массопередач концентрации фазы L по аналогии можно получить ;

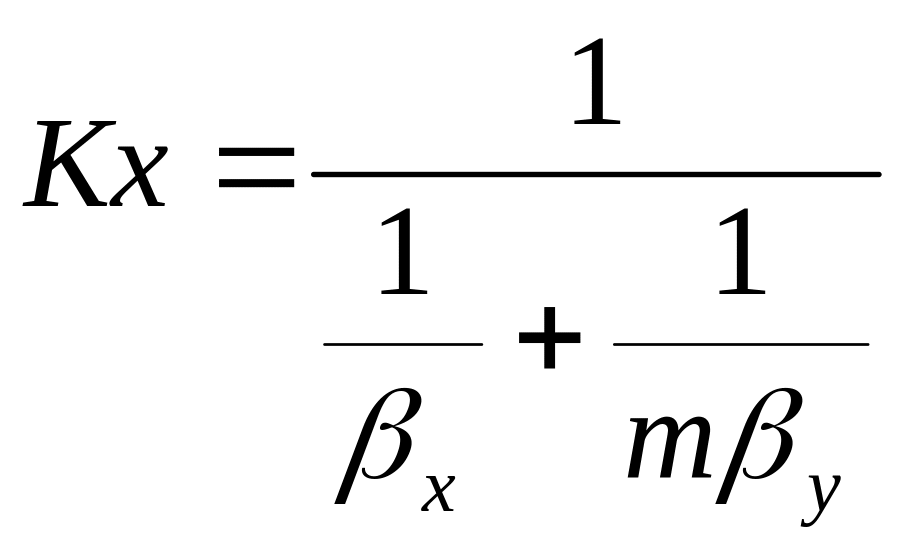m- коэф-т распределения .

87. Подобие диффузионных процессов. При выборе условий и критериев диф-го подобия исходят из ДУ молекулярного и конвективного массопереноса в-ва. В свою очередь сходство ДУ массо и тепло переноса дает основание пологать, что критерий диф-го и теплового подобия имеет одинаковый вид. В этом легко убедиться, анализируя условия массообмена у границы разделе фаз. Кол-во распред-го в-ва, переносимого от пов-ти контакта в ядро потока можно выразить с помощью Ур-я массоотдачи в свою очереть массоперенос в пограничном слое, где приобладает молекул-я диф-я, описывается Ур-ем Фика: . Приравниваем правые части Ур-ий, получим выражение, хар-е граничные условия при массопереноса . Это выражение явл-ся з-ном сохранения в-ва. Переходя к конкретным хар-ым величинам и отбрасывая знаки мат-их операторов будем иметь: Разделив левую часть на правую получим безразмерный комплекс , который в подобных системах идентичен и назван диффузионным числом Нуссельта (Nu’) - диф-е число Нуссельта.Диф-й критерий Нуссельта хар-ет соотношение хар-го размера в толщине пограничного слоя. Для установления диф-го подобия в ядре потока, за исходную позицию берут ДУ конвективного массообмена. Для кратности изложения запишем одномерное, нестац-е Ур-е диффузии:

Проводя замену членов ДУ конечной величины отбросив при этом знаки математ-их операторов получим: . Разделив правую часть Ур-я на 1-е слогаемое в левой части получим безразмерный комплекс , который для подобных процессов идентичный, и назван диф-ым числом Фурье: - идентичное число Фурье. Число Фурье хар-ет подобие нестационарных процессов. Поделив 2-е слагаемое предыдущего выражения на правую часть, получим безразмерный комплекс , который для диф-ых процессов идентичен и назван диф-ым критерием Пекле: 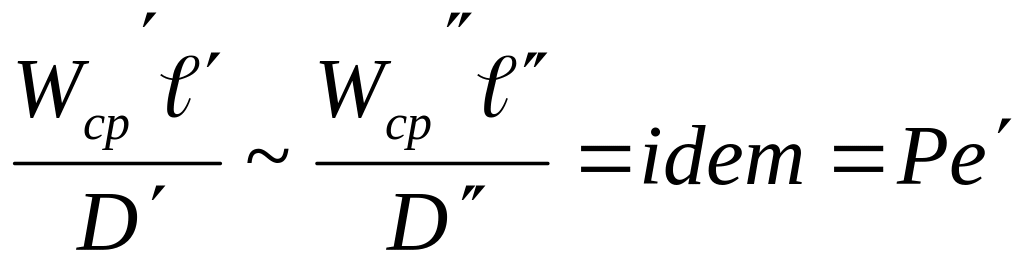- диф-е число Пекле. Число Пекле хар-ет соотношение массовых потоков за счет конвекции и диффузии. Если умножить числитель и знаменатель в числе Пекле на отношение , то получим: , где - число Прандля диф-е, хар-ие физ-е св-ва в-в в фазах и указывет на соотношение между толщинами гидродинамического и диф-ых слоев.Полученные из ДУ числа подобия позволяют записать критериальное Ур-е в неявной форме: . Из всех чисел диф-го подобия, включающих первоначальные величины в число Nu входит величина , которая сама зависит от нескольких переменных и явл-ся искомой. Следовательно критерий Nu явл-ся определенным критерием, а остальные- определяющие. В связи с этим критериальные Ур-я представляют в таком виде: . Явный вид данного Ур-я устан-ся как правило при обработке эксперем-ых данных, различными методами.

88.вывод критериев диф-го подобия Nu, Pe,Pr При выборе условий и критериев диф-го подобия исходят из ДУ молекулярного и конвективного массопереноса в-ва. В свою очередь сходство ДУ массо и тепло переноса дает основание пологать, что критерий диф-го и теплового подобия имеет одинаковый вид. В этом легко убедиться, анализируя условия массообмена у границы разделе фаз. Кол-во распред-го в-ва, переносимого от пов-ти контакта в ядро потока можно выразить с помощью Ур-я массоотдачи в свою очереть массоперенос в пограничном слое, где приобладает молекул-я диф-я, описывается Ур-ем Фика: . Приравниваем правые части Ур-ий, получим выражение, хар-е граничные условия при массопереноса . Это выражение явл-ся з-ном сохранения в-ва. Переходя к конкретным хар-ым величинам и отбрасывая знаки мат-их операторов будем иметь: Разделив левую часть на правую получим безразмерный комплекс , который в подобных системах идентичен и назван диффузионным числом Нуссельта (Nu’) - диф-е число Нуссельта.Диф-й критерий Нуссельта хар-ет соотношение хар-го размера в толщине пограничного слоя. Для установления диф-го подобия в ядре потока, за исходную позицию берут ДУ конвективного массообмена. Для кратности изложения запишем одномерное, нестац-е Ур-е диффузии:

Проводя замену членов ДУ конечной величины отбросив при этом знаки математ-их операторов получим: . Разделив правую часть Ур-я на 1-е слогаемое в левой части получим безразмерный комплекс , который для подобных процессов идентичный, и назван диф-ым числом Фурье: - идентичное число Фурье. Число Фурье хар-ет подобие нестационарных процессов. Поделив 2-е слагаемое предыдущего выражения на правую часть, получим безразмерный комплекс , который для диф-ых процессов идентичен и назван диф-ым критерием Пекле: - диф-е число Пекле. Число Пекле хар-ет соотношение массовых потоков за счет конвекции и диффузии. Если умножить числитель и знаменатель в числе Пекле на отношение , то получим: , где - число Прандля диф-е, хар-ие физ-е св-ва в-в в фазах и указывет на соотношение между толщинами гидродинамического и диф-ых слоев.Полученные из ДУ числа подобия позволяют записать критериальное Ур-е в неявной форме: . Из всех чисел диф-го подобия, включающих первоначальные величины в число Nu входит величина , которая сама зависит от нескольких переменных и явл-ся искомой. Следовательно критерий Nu явл-ся определенным критерием, а остальные- определяющие. В связи с этим критериальные Ур-я представляют в таком виде: . Явный вид данного Ур-я устан-ся как правило при обработке эксперем-ых данных, различными методами.

89. Вид критериальных зав-тей в явной и неявной форме. При выборе условий и критериев диф-го подобия исходят из ДУ молекулярного и конвективного массопереноса в-ва. В свою очередь сходство ДУ массо и тепло переноса дает основание пологать, что критерий диф-го и теплового подобия имеет одинаковый вид. В этом легко убедиться, анализируя условия массообмена у границы разделе фаз. Кол-во распред-го в-ва, переносимого от пов-ти контакта в ядро потока можно выразить с помощью Ур-я массоотдачи в свою очереть массоперенос в пограничном слое, где приобладает молекул-я диф-я, описывается Ур-ем Фика: . Приравниваем правые части Ур-ий, получим выражение, хар-е граничные условия при массопереноса . Это выражение явл-ся з-ном сохранения в-ва. Переходя к конкретным хар-ым величинам и отбрасывая знаки мат-их операторов будем иметь: Разделив левую часть на правую получим безразмерный комплекс , который в подобных системах идентичен и назван диффузионным числом Нуссельта (Nu’) - диф-е число Нуссельта.Диф-й критерий Нуссельта хар-ет соотношение хар-го размера в толщине пограничного слоя. Для установления диф-го подобия в ядре потока, за исходную позицию берут ДУ конвективного массообмена. Для кратности изложения запишем одномерное, нестац-е Ур-е диффузии:

Проводя замену членов ДУ конечной величины отбросив при этом знаки математ-их операторов получим: . Разделив правую часть Ур-я на 1-е слогаемое в левой части получим безразмерный комплекс , который для подобных процессов идентичный, и назван диф-ым числом Фурье: - идентичное число Фурье. Число Фурье хар-ет подобие нестационарных процессов. Поделив 2-е слагаемое предыдущего выражения на правую часть, получим безразмерный комплекс , который для диф-ых процессов идентичен и назван диф-ым критерием Пекле: - диф-е число Пекле. Число Пекле хар-ет соотношение массовых потоков за счет конвекции и диффузии. Если умножить числитель и знаменатель в числе Пекле на отношение , то получим: , где - число Прандля диф-е, хар-ие физ-е св-ва в-в в фазах и указывет на соотношение между толщинами гидродинамического и диф-ых слоев.Полученные из ДУ числа подобия позволяют записать критериальное Ур-е в неявной форме: . Из всех чисел диф-го подобия, включающих первоначальные величины в число Nu входит величина , которая сама зависит от нескольких переменных и явл-ся искомой. Следовательно критерий Nu явл-ся определенным критерием, а остальные- определяющие. В связи с этим критериальные Ур-я представляют в таком виде: . Явный вид данного Ур-я устан-ся как правило при обработке эксперем-ых данных, различными методами