§ 12.4. Исследование систем методом функций Ляпунова

С помощью функций Ляпунова обычно оценивается, прежде всего, устойчивость некоторого положения равновесия. В случае положительного результата ищется область притяжения этого положения; в некоторых случаях может оцениваться длительность времени затухания нормы решения, соответствующего некоторым начальным условиям. Для решения этих задач необходимо, во-первых, найти положения равновесия исследуемой системы, во-вторых, записать её уравнения в отклонениях от заданного положения равновесия (см. §§ 10.2, 12.2) и, в третьих, построить или выбрать функцию Ляпунова для исследуемой системы. Так как указанные задачи проще всего решаются при функции Ляпунова в виде квадратичной формы, то функцию Ляпунова выбирают чаще всего именно в этой форме, т.е. в виде (12.12) при соответствующем n.

Покажем на конкретных примерах методику исследования устойчивости с помощью функций Ляпунова.

Пример 12.3. Исследовать устойчивость положения равновесия системы, если её уравнения в отклонениях имеют вид

, .

Решение. Так как уравнения системы в отклонениях и положение равновесия заданы, то сразу переходим к выбору функции Ляпунова. Возьмем функцию , т.е. в виде квадратичной формы. Ее производная вдоль траекторий рассматриваемой системы, согласно (12.16), (12.17), определяется выражением

или

.

Полученная функция является определенно-отрицательной при всех . Следовательно, функция является функцией Ляпунова для рассматриваемой системы. Причём она удовлетворяет условиям теоремы 12.1 при всех . Поэтому положение равновесия рассматриваемой системы является аттрактором и асимптотически устойчиво в целом. ■

Пример 12.4. Исследовать методом функций Ляпунова устойчивость линейной системы, уравнение свободного движения которой в отклонениях имеет вид

. (12.19)

Решение. В данном случае можно говорить об устойчивости системы, поскольку она является линейной. Положением равновесия её является точка . В случае линейных систем функция Ляпунова ищется обычно в виде квадратичной формы , где Р – симметрическая матрица.

Найдем ее производную по времени на траекториях системы (12.19). Дифференцируя её по времени, как сложную функцию двух аргументов и , получим

.

В соответствии с уравнением (12.19) , поэтому

, (12.20)

где С – симметрическая матрица. Из выражения (12.20) вытекает следующее равенство:

, (12.21)

которое называется уравнением Ляпунова. В нём Р и С – симметрические матрицы, причем С всегда положительно-определённая матрица, т.е. С > 0.

При исследовании устойчивости динамических систем в уравнении Ляпунова обычно задаются матрицей C, а матрицу P находят как решение этого уравнения. Ляпунов доказал следующее утверждение.

Теорема 12.7. Если при С > 0 решение уравнения (12.21) – матрица P является положительно-определённой, то линейная система (12.19) асимптотически устойчива в целом. Если же матрица Р окажется отрицательно-определённой, то система (12.19) является неустойчивой. ■

Отметим, что математическое обеспечение современных ЭВМ имеет специальные программы для решения уравнения Ляпунова. Например, в системе MATLAB это программа “Lyap”.

Уравнение Ляпунова (12.21) часто применяется для исследования устойчивости и построения области притяжения (рис. 12.5) положения равновесия нелинейных систем

вида

, (12.22)

где А – устойчивая матрица, – нелинейная вектор-функция, причём . Если , то её производная вдоль траекторий системы (12.22) определяется выражением

. (12.23)

Здесь матрицы Р и С из уравнения Ляпунова (12.21).

Если удаётся показать, что в некоторой области , включающей точку , модуль первого слагаемого в (12.23) больше модуля второго слагаемого, то в этой области, очевидно, будут выполнены условия теоремы 12.1. Следовательно, при всех начальных условиях таких, что решения системы (12.22) не выходят из области , свободное движение этой системы будет затухающим.

В этом случае положение равновесия нелинейной системы (12.22) будет асимптотически устойчивым в большом. Указанная область является областью устойчивости или областью притяжения положения равновесия рассматриваемой нелинейной системы (12.22). На рис. 12.5 область притяжения – это не заштрихованная область.

Пример 12.5. Исследовать устойчивость положения равновесия системы, показанной на рис. 12.6, двумя (первым и вторым) методами Ляпунова, если , а y – выходная переменная.

Решение. Прежде всего, найдем уравнения заданной системы в переменных состояния. В соответствии с рис. 12.6 имеем равенства, , . Переходя к оригиналам, получим . Отсюда , так как . Пусть , тогда . Следовательно, уравнения рассматриваемой системы в форме (12.4) имеют вид

, . (12.24)

Для определения положений равновесия (особых точек) заданной системы, следуя примеру 10.1, запишем уравнения особых точек: , . Отсюда следует, что положением равновесия исследуемой системы является точка , а уравнениями в отклонениях – выражения (12.24).

Метод первого приближения. Для исследования устойчивости этим методом необходимо, как показано выше, сначала построить уравнения первого приближения. С этой целью по формулам (12.8) находим

, , , .

Итак, уравнение первого приближения (12.7) заданной системы (12.24) имеет вид

.

Характеристический полином этой системы

,

а его корни , . Так как один из корней равен нулю, то сделать какое-либо заключение об устойчивости или неустойчивости системы (12.24) по уравнениям первого приближения, в соответствии с теоремой 12.3, нельзя.

Метод функций Ляпунова. В качестве функции Ляпунова возьмем функцию . Ее производная по времени вдоль траекторий системы (12.24) определяется следующим образом:

.

Очевидно, функции и не удовлетворяют ни четвёртой ни пятой теоремам Ляпунова. При этом функция является бесконечно большой, а функция обращается в нуль при и любом . Таким образом, функция из условия Барбашина (12.18) здесь имеет вид при . Подставляя эту функцию в условие Барбашина (12.18), с учетом уравнений системы (12.24), получим . Это неравенство, очевидно, выполняется на линии, где , т.е. при всех и . Таким образом, функция удовлетворяет всем условиям теоремы Барбашина-Красовского при всех и . Следовательно, в силу этой теоремы положение равновесия исследуемой нелинейной системы (рис. 12.6) асимптотически устойчиво в целом. ■

Заметим, что в ряде случаев установить наличие целых траекторий системы на поверхности достаточно сложно. Следующий пример подтверждает это.

Пример 12.7. Исследовать устойчивость положения равновесия системы, свободное движение которой описывается уравнением:

. (12.25)

Решение. Прежде всего, представим уравнение (12.25) в переменных состояния. Пусть , а 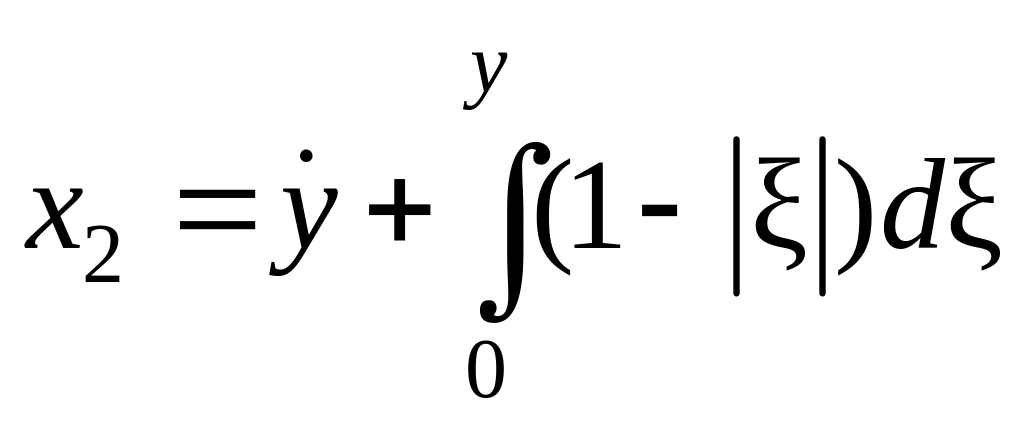. Их производные по времени

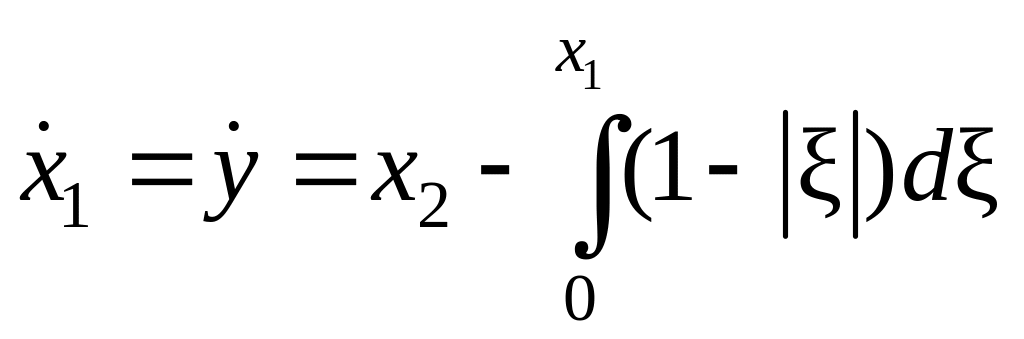, а .

Подставляя во второе равенство выражение для из уравнения (12.25), получим

.

Итак, уравнению «вход-выход» (12.25) можно поставить в соответствие следующие уравнения в переменных состояния:

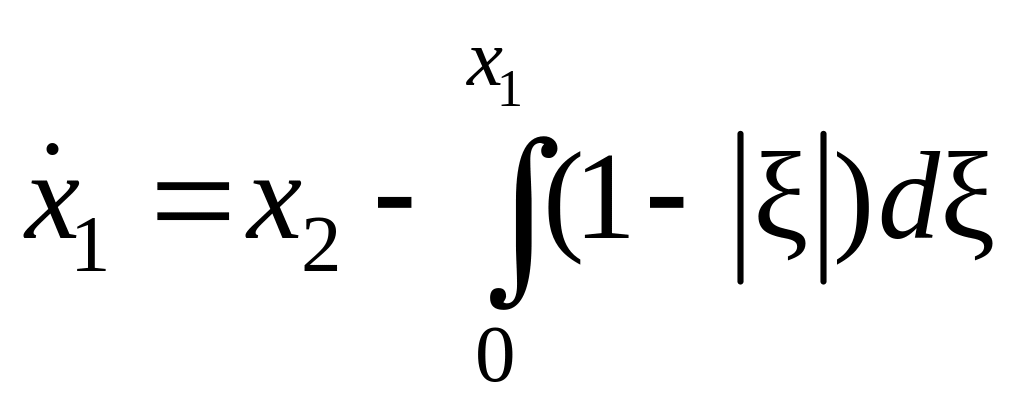, . (12.26)

Положением равновесия системы (12.26) очевидно также является точка . В качестве функции Ляпунова и в этом примере возьмём бесконечно большую функцию . Её производная по времени вдоль траекторий системы (12.26) описывается следующим выражением:

.

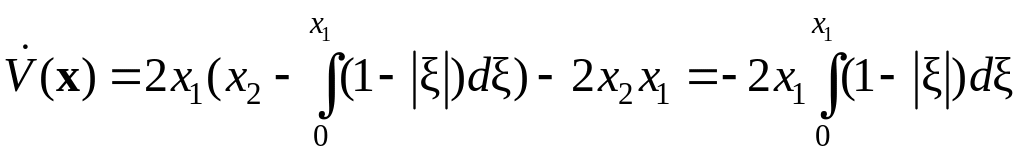Произведение

,

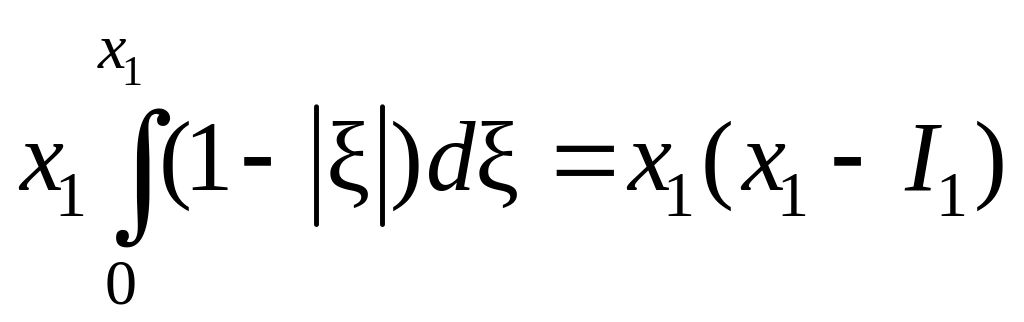где

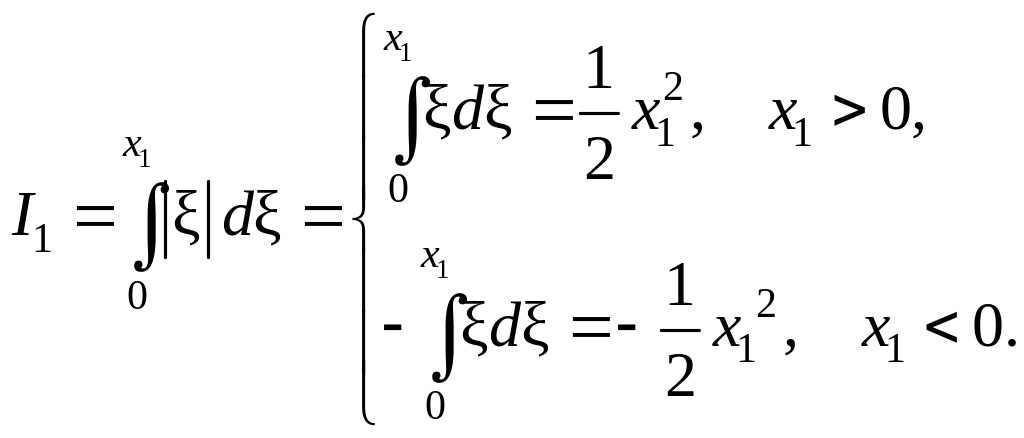
Следовательно,

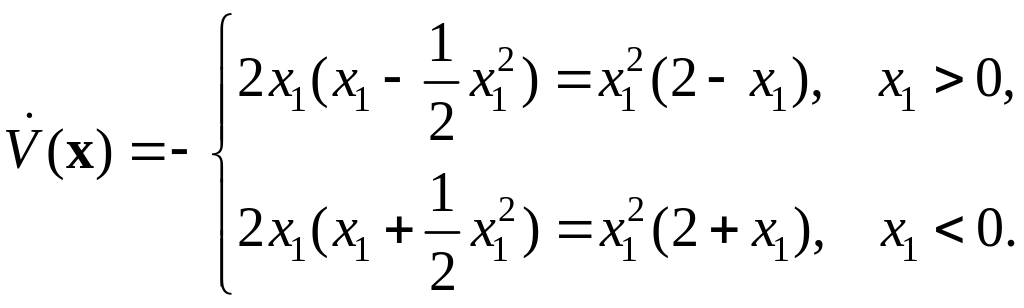
Полученная функция также является отрицательно полуопределенной, причем функция обращается в нуль на линиях и , при . Следовательно, функция из условия Барбашина (12.18) здесь имеет вид . Соответственно, функция Барбашина

.

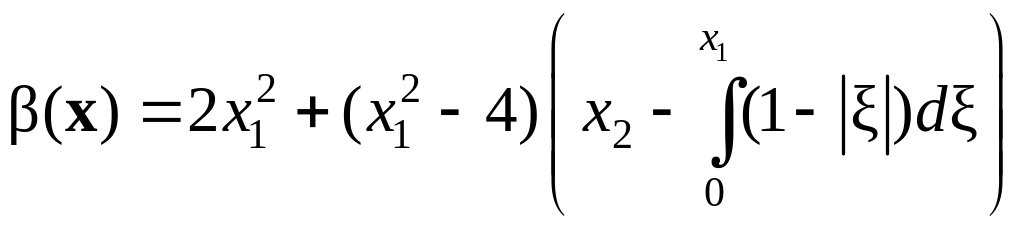На линии , эта функция , а на линии , функция тоже, т.е. условие (12.18) выполняется во всех точках, где . Легко убедиться также, что точки линий и , не являются решениями системы (12.26), подставив эти значения и в уравнения. Следовательно, можно сделать вывод, что в полосе , выполняются все условия теоремы Барбашина-Красовского.

Однако помимо непериодических решений, полоса может включать точки циклов рассматриваемой системы, которые являются решением системы (12.26). Так как определение последних затруднительно, то определить область устойчивости рассматриваемой системы с помощью данной функции Ляпунова и теоремы Барбашина-Красовского достаточно сложно. Можно лишь утверждать, что в силу теоремы Барбашина-Красовского положение равновесия системы (12.26), а значит и уравнения (12.25) является асимптотически устойчивым в области , , где m – некоторое число. Его значение можно установить дополнительными исследованиями.

Действительная область притяжения системы, описываемой уравнением (12.25), легко определяется (поскольку порядок системы равен двум) по фазовому портрету, который построен в MATLAB и приведён на рис. 12.7, где , а . Как видно, она ограничена неустойчивым циклом и включает отрезок оси . ■