§ 12.2. Метод первого приближения

А.М. Ляпунов в своей докторской диссертации, в частности, нашел и теоретически обосновал условия применимости метода первого приближения (применявшегося и ранее) для исследования устойчивости движений нелинейных систем n-го порядка. При исследовании нелинейных систем этим методом по уравнению (12.4) строятся, как отмечалось в § 10.2, уравнения первого приближения:

, , (12.7)

где

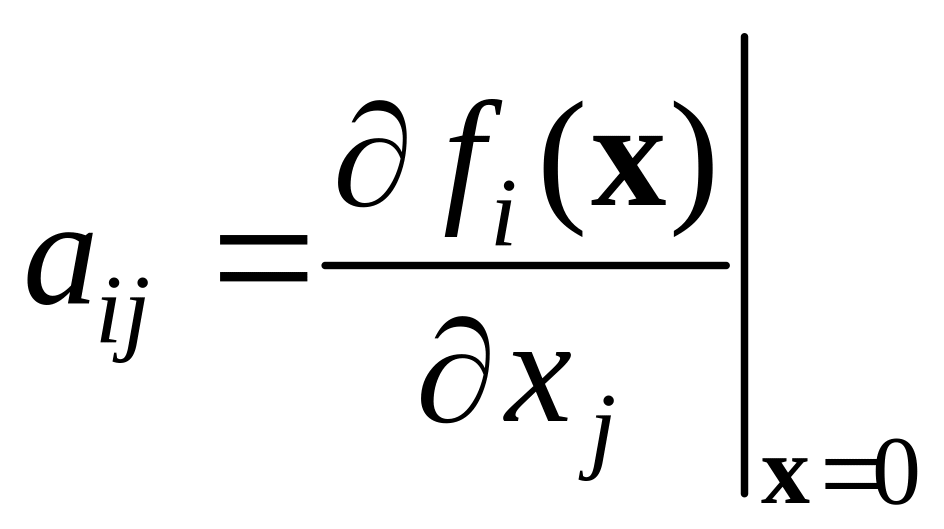, . (12.8)

Ляпуновым были доказаны теоремы, позволяющие установить устойчивость или неустойчивость невозмущенного движения нелинейной системы (12.1) или, что тоже самое положения равновесия системы (12.4), путем исследования её уравнений первого приближения (12.7), (12.8). Обычно этот способ называют или первым методом Ляпунова, или методом первого приближения, или методом линеаризации. Он может быть применен к исследованию нелинейной системы (12.4), если только – непрерывная, дифференцируемая вектор-функция, а отклонения малы по норме, т.е. , где – некоторое малое число.

Далее под нормой будет пониматься одно из следующих выражений:

или . (12.9)

Уравнения (12.7) часто называются линейными уравнениями в отклонениях или уравнениями первого приближения.

Теоремы Ляпунова метода первого приближения. Обозначим через , корни характеристического уравнения системы первого приближения (12.7). А. М. Ляпунов доказал следующие теоремы.

Теорема 12.1 (об асимптотической устойчивости). Если вещественные части всех

корней характеристического уравнения системы первого приближения (12.7) строго меньше нуля, т.е.

, (12.10)

то невозмущенное движение нелинейной системы (12.1) и положение равновесия системы (12.4) асимптотически устойчивы в малом. ■

Определение. Если при , где – достаточно малое число, выполняются условия

, , (12.11)

где – некоторое число, зависящее от , то положение равновесия системы (12.4) называется асимптотически устойчивым в малом. ■

Ситуация, соответствующая условиям (12.11), показана на рис. 12.2.

Определение. Область начальных значений, при которых выполняются условия (12.11), называется областью притяжения или областью асимптотической устойчивости положения равновесия системы (12.4). ■

Например, областью притяжения на рис. 12.3 является внутренняя область замкнутой кривой, показанной пунктирной линией. Само положение равновесия (0, 0) в данном случае называется аттрактором (т.е. притягивающим положением равновесия).

Определение. Если областью притяжения положения равновесия некоторой системы является все фазовое пространство, то она называется асимптотически устойчивой в целом. ■

Отметим, что любая матрица , корни характеристического уравнения которой удовлетворяют условию (12.10), называется устойчивой матрицей. При этом условии система (12.7) является асимптотически устойчивой в целом.

Теорема 12.2 (о неустойчивости по первому приближению). Если среди корней характеристического уравнения системы первого приближения (12.7) найдётся хотя бы один с положительной вещественной частью, т.е.

, , (12.12)

то невозмущенное движение нелинейной системы (12.1) и положение равновесия системы (12.4) являются неустойчивыми, т.е. условия (12.11) не выполняются. ■

Теорема 12.3 (о невозможности исследования устойчивости по первому приближению). Если среди корней характеристического уравнения системы первого приближения имеется один или несколько с нулевыми вещественными частями, а остальные корни имеют отрицательную вещественную часть, то об устойчивости или неустойчивости невозмущенного движения нелинейной системы (12.1) и положения равновесия системы (12.4) сказать ничего нельзя. ■

Пример 12.1. Исследовать зависимость устойчивости положения равновесия от параметра α системы, которая описывается следующими уравнениями в отклонениях:

, .

Решение. Прежде всего, построим систему первого приближения (12.7) в окрестности заданного положения равновесия. С этой целью найдем коэффициенты матрицы с помощью соотношений (12.8):

, ,

, .

Следовательно, система первого приближения в данном случае имеет вид

.

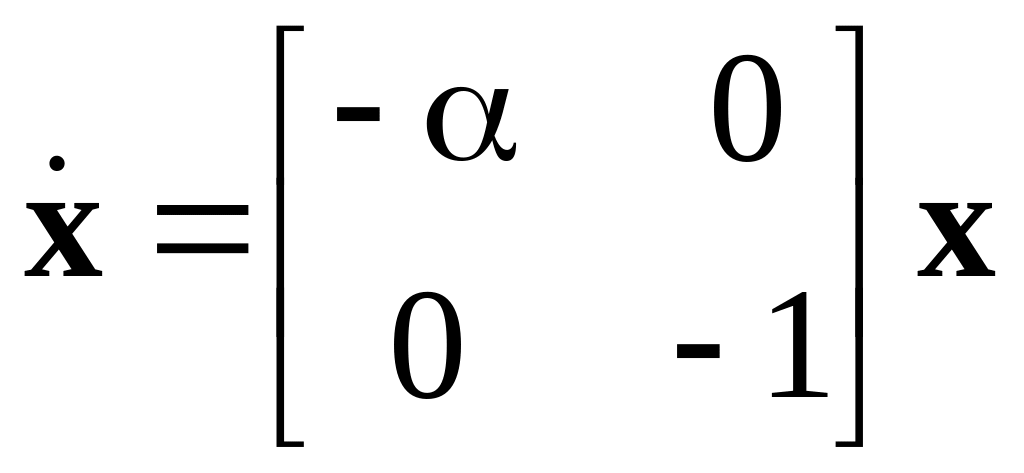Корни характеристического уравнения системы первого приближения в этом примере, очевидно, равны , . Применяя теперь теоремы Ляпунова, приходим к следующим выводам:

а) при , все корни характеристического уравнения имеют отрицательную вещественную часть. Поэтому, в соответствии с теоремой 12.1, положение равновесия исследуемой нелинейной системы асимптотически устойчиво в малом;

б) при , один корень характеристического уравнения имеет положительную вещественную часть, т.е. в соответствии с теоремой 12.2, положение равновесия исследуемой нелинейной системы является неустойчивым;

в) при , один корень характеристического уравнения равен нулю, поэтому в соответствии с теоремой 12.3, нельзя сделать каких-либо заключений об устойчивости или неустойчивости положения равновесия рассматриваемой нелинейной системы. ■

Большим преимуществом первого метода Ляпунова является простота процедуры исследования устойчивости положения равновесия. Это связано с тем, что к исследованию устойчивости положений равновесия нелинейных систем фактически применяются критерии устойчивости линейных систем. Однако метод первого приближения может использоваться, если только нелинейности системы являются дифференцируемыми функциями по всем своим аргументам.

Недостатком метода первого приближения является также и то, что приведенные выше теоремы позволяют оценить лишь устойчивость в малом, т.е. только лишь в сколь угодно малой области отклонений состояния системы от её положения равновесия. При этом определить величину этой области данный метод не позволяет.