Если условия (11.16) или (11.17), (11.18) выполняются по отношению к некоторой нелинейной системе, то в этой системе возможны периодические движения, которые называются автоколебаниями, т.е. собственными периодическими движениями системы. Другими словами, такая система является генератором незатухающих периодических колебаний.

Если в системе существуют автоколебания, то возникает задача определения их параметров (амплитуды и частоты). Для решения этой задачи условие (11.16) записывается следующим образом:

. (11.19)

В соответствии с равенством (11.19) для установления факта отсутствия автоколебаний или их возможного существования достаточно на комплексной плоскости построить годограф Найквиста и годограф . Если эти годографы не пересекаются (рис. 11.11, случай системы с ), то автоколебаний в системе не возникнет, и можно заключить, что положение равновесия рассматриваемой нелинейной системы устойчиво. В этом случае исследование заданной нелинейной системы методом гармонической линеаризации завершается. Если же годографы и пересекаются, то автоколебания возможны. При этом их параметры определяются значениями амплитуды и частоты , которые соответствуют точкам пересечения этих годографов.

Чаще всего точек пересечения годографов, как видно на рис. 11.11, несколько. В случае системы с и это точки, соответствующие , и , . Поэтому для определения амплитуды и частоты автоколебаний, которые действительно устанавливаются в системе, необходимо оценить устойчивость всех возможных автоколебаний. Однако, прежде чем переходить к оценке устойчивости автоколебаний, необходимо найти их параметры. Обычно для этого необходимо решить нелинейное алгебраическое уравнение, в которое переходит условие (11.19) после подстановки в него соответствующих выражений.

§ 11.3. Оценка устойчивости автоколебаний

Для решения этой задачи целесообразно воспользоваться критерием Найквиста. Как известно, по этому критерию, если система находится на границе устойчивости, то годограф Найквиста системы проходит через точку комплексной плоскости, т.е. выполняется условие , где – комплексный коэффициент передачи системы в разомкнутом состоянии. Именно эта ситуация имеет место и в нелинейной системе, когда её характеристики соответствуют годографам и (см. рис. 11.11). При этом в точках пересечения этих годографов выполняется условие , причем левая часть этого равенства, очевидно, представляет собой комплексный коэффициент передачи рассматриваемой системы в разомкнутом состоянии.

Примем для определённости, что с увеличением соответствующая этому значению амплитуды точка годографа перемещается в направлении от к , как

показано на рис. 11.11 и на рис. 11.12,а стрелкой.

Предположим также, что в рассматриваемой системе установились колебания с частотой и амплитудой . Так как системы всегда подвержены различным воздействиям,

то амплитуда колебаний может стать, скажем, меньшей чем . Тогда точка на годографе , соответствующая этим новым колебаниям с амплитудой , будет располагаться вне годографа (см. рис. 11.12,а), т.е. не будет охватываться им. В соответствии с критерием Найквиста, это новое состояние нелинейной системы соответствует устойчивой линейной системе, в которой всякие колебания затухают. Следовательно, с течением времени амплитуда колебаний будет уменьшаться, т.е. движение системы будет все более отклоняться от автоколебаний с параметрами , .

Аналогично, если амплитуда под действием возмущений примет значение , большее чем , то соответствующая ей точка на годографе будет охватываться годографом Найквиста . В этом случае, в соответствии с тем же критерием Найквиста, нелинейная система будет эквивалентна линейной неустойчивой системе, в которой амплитуда колебаний нарастает с течением времени. Следовательно, и в этом случае движение системы будет все более отклоняться от автоколебаний с параметрами и . Поэтому эти колебания будут неустойчивыми и, существовать продолжительное время в нелинейной системе они не могут.

В то же время, повторяя приведённые рассуждения, можно убедиться, что автоколебания с параметрами , в рассматриваемой системе являются асимптотически устойчивыми, так как возникающие отклонения амплитуды колебаний от будут уменьшаться до нулевых значений. Поэтому в рассматриваемой нелинейной системе с и установятся автоколебания с параметрами и .

Заметим, что аналогичная ситуация имеет место в системе второго порядка, фазовый портрет которой имеет два цикла, вложенных друг в друга, как показано на рис. 11.12,б. При этом внутренний цикл является неустойчивым, а внешний – устойчивым. Поэтому, если начальные условия таковы, что изображающая точка при лежит внутри внутреннего цикла, то последующее движение будет затухающим и автоколебаний не возникает. Говорят, система не возбуждается.

Если же начальные условия (начальный толчок) таковы, что изображающая точка при

окажется вне внутреннего цикла, но внутри внешнего, то в дальнейшем амплитуда колебаний нарастает и движение системы постепенно приближается к периодическому, которое соответствует внешнему устойчивому циклу. В результате в системе устанавливаются автоколебания.

Для исследования устойчивости автоколебаний гармонически линеаризованных систем можно также применять вытекающий из изложенного следующий критерий.

Критерий устойчивости автоколебаний. Если при увеличении амплитуды колебаний годограф нелинейного элемента пересекает годограф линейной части извне вовнутрь, то точке пересечения соответствуют неустойчивые автоколебания, если же – изнутри вовне, то – устойчивые автоколебания. ■

Для завершения исследования свойств нелинейной системы методом гармонической линеаризации необходимо, если выполняется условие (11.19), проверить выполнимость гипотезы фильтра. Для этого необходимо вычислить и сравнить значения и , где – частота устойчивых автоколебаний.

Если , то гипотеза фильтра будет выполняться, и в системе будут существовать автоколебания с параметрами, близкими к полученным в результате расчетов. В противном случае никаких выводов о свойствах системы на основе проведённых в соответствии с методом гармонической линеаризации расчетов сделать нельзя.

Пример 11.1. Проверить возможность существования автоколебаний в системе, структурная схема которой приведена на рис. 11.13. Передаточные функции линейных звеньев и параметры нелинейного элемента определяются следующими выражениями:

, , .

Если колебания возможны, то определить их параметры. Оценить устойчивость возможных автоколебаний; проверить, выполняется ли гипотеза фильтра, и сделать выводы о свойствах движений данной системы.

Решение. В соответствии со схемой на рис. 11.13 и формулой (11.12) можно записать

, . (11.20)

Так как – вещественная положительная функция, то пересечение годографов и возможно лишь на отрицательной вещественной полуоси, которую годограф пересекает при , как показано на рис. 11.14. На этом рисунке годограф (11.20) для наглядности условно показан в виде двух прямых, параллельных полуоси и соединенных дугой. На самом деле обе эти ветви годографа совпадают с полуосью , а точки и совпадают с точкой ω_π. Отметим, что переход с одной ветви на другую происходит при . В связи с тем, что в рассматриваемой системе точки и совпадают с точкой ω_π, сначала найдем частоту ω_π. На этой частоте мнимая часть комплексного коэффициента равна нулю, поэтому, полагая в знаменателе первого выражения (11.20) разность , найдём отсюда .

Взаимное расположение годографов и , фигурирующих в условии (11.19), показано на рис. 11.14. Из условия их пересечения при и выражений (11.20) имеем уравнение

.

Графическое решение этого уравнения показано на рис. 11.15. Как видно, это уравнение имеет два корня: и (найдены аналитически). Следовательно, в системе возможны автоколебания либо с амплитудой и частотой , либо с амплитудой и частотой .

Анализ устойчивости этих автоколебаний с помощью приведённого выше критерия приводит к выводу, что автоколебания с меньшей амплитудой неустойчивы, а с большей – устойчивы. Поэтому заключаем, что в данной системе могут установиться автоколебания с частотой и амплитудой . Условием возникновения автоколебаний являются достаточно большие начальные условия.

Однако эти заключения будут справедливы, если выполняется гипотеза фильтра. Для проверки гипотезы фильтра найдём значение амплитудно-частотной характеристики линейной части системы на частоте автоколебаний и и сравним результаты.

Имеем , а , т.е. в четыре раза больше, чем . Следовательно, гипотеза фильтра выполняется, но недостаточно полно. Можно заключить, что автоколебания возникнут, но их амплитуда будет несколько отличаться от расчетной. ■

Пример 11.2. Найти ошибку , обусловленную автоколебаниями, возникающими в системе, рассмотренной в примере 11.1.

Решение. Для определения указанной ошибки примем во внимание, что определённые в соответствии с методом гармонической линеаризации параметры и – это амплитуда и частота переменной на входе нелинейного элемента.

С другой стороны, в соответствии со схемой рассматриваемой системы, приведенной на рис. 11.13, переменная является выходной переменной линейного звена с передаточной функцией

.

Ко входу этого звена приложено отклонение рассматриваемой системы, которое имеет колебательный характер. Амплитуда этого отклонения и является, очевидно, искомой ошибкой. Следовательно, можно записать равенство

.

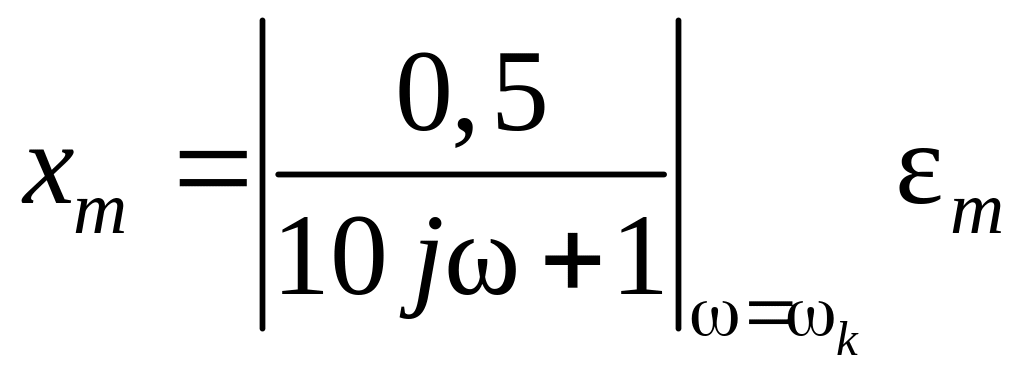Отсюда, с учетом найденных значений частоты и амплитуды автоколебаний, находим . Как видно, несмотря на то, что зона нечувствительности нелинейного элемента всего лишь 0,01, ошибка, обусловленная автоколебаниями, возникающими в рассматриваемой системе, довольно значительна. В данном случае она более чем в 60 раз превышает зону нечувствительности нелинейного элемента. ■

В связи с этим при проектировании систем автоматического управления всегда стремятся исключить возможность существования автоколебаний. Для этой цели можно воспользоваться частотными методами коррекции, которые позволяют изменить годограф линейной части нелинейной системы в окрестности частоты (см. рис. 11.14) так, чтобы годографы линейной и нелинейной частей системы не пересекались.

В заключение этой главы отметим, что метод гармонической линеаризации может применяться для анализа нелинейных систем не только второго, но и более высоких порядков. Его можно использовать, в частности, для исследования свойств несимметричных автоколебаний, т.е. автоколебаний с постоянной составляющей [15].

Г л а в а 12

ИССЛЕДОВАНИЕ НЕЛИНЕЙНЫХ СИСТЕМ МЕТОДАМИ ЛЯПУНОВА