3. Лопаточный коэффициент полезного действия

3.1. Вводные замечания и определения

Лопаточным коэффициентом полезного действия (кпд) называют от­ношение полезной работы на лопаточном венце полностью уплотненной ступени к располагаемой работе, величина которой определяется состо­янием рабочего тела перед ступенью и давлением за ступенью.

Обозначим:

- лопаточный кпд;

- полезная работа (полезно использованный перепад энтальпий);

- располагаемая работа (располагаемый перепад энтальпий).

Тогда по определению:

. (3.1)

Полезно использованный в ступени перепад энтальпий [см. форму­лу (2.27)]

или с учетом формулы (2.2)

, (3.2)

где - располагаемый перепад энтальпий в ступени, определенный по статическим параметрам перед ней и статическому давлению за ней; - перепад энтальпий, соответствующий кинетической энергии потока на входе в ступень; - необратимые потери ме­ханической энергии в сопловых лопатках («потери в соплах»); - то же в рабочих лопатках; - перепад энтальпий, со­ответствующий кинетической энергии потока на выходе из ступени, или, как чаще говорят, потери с выходной скоростью.

Выражение (3.2) является уравнением баланса энергии для турбинной ступени. С другой стороны, в соответствии с турбинным уравнением Эйлера для 1 кг рабочего тела полезная работа опре­деляется формулой (1.8). Следует отметить, что уравнения (3.2) и (1.8) - лишь различные формы записи одной и той же физической ве­личины и могут быть преобразованы одно в другое путем алгебраичес­ких выкладок.

Решение вопроса о выборе величины располагаемого перепада в ступени не однозначно. За располагаемый перепад принимают в разных случаях: величину , названную выше (рис.3.1,а), величину (рис.3.1,б), величину (рис.3.1,в).

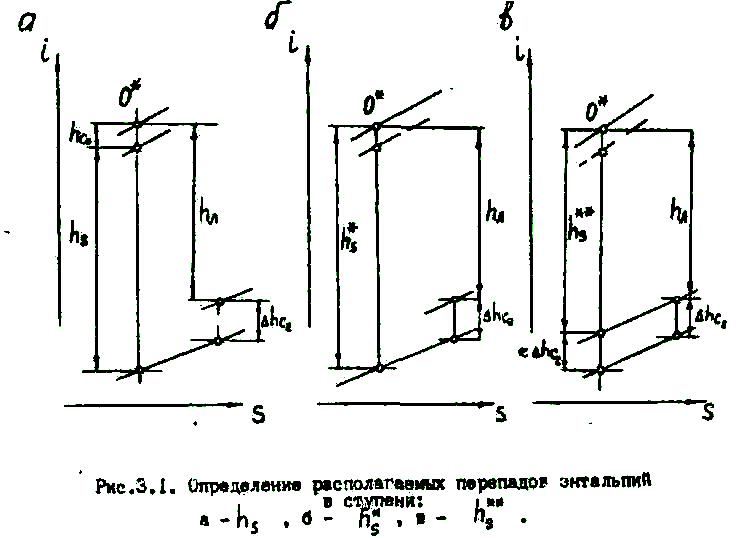
В общем случае, при работе турбинной ступени в группе, в ней используется кинетическая энергия потока, поступающего из предыду­щей ступени.

С этой точки зрения выбор располагаемых перепадов, показанных на рис.3.1, соответствует предельным теоретически возможным случаям.

Поэтому выражение для располагаемого перепада иногда записывается в таком виде:

, (3.3)

где - коэффициент использования в данной ступени кинетичес­кой энергии потока, выходящего из предыдущей ступени; - коэф­фициент использования в последующей ступени кинетической энергии потока, выходящего из данной ступени.

Практически кинетическая энергия потока на входе в ступень используется в различной степени. Для простоты целесообразно огра­ничиться приведенными предельными трактовками .

Располагаемые перепады и другие величины, определенные на ба­зе формулы (3.3) для рассмотренных выше предельных случаев, пока­заны в табл.3.1.

Принятым различным трактовкам располагаемого перепада ступени соответствуют и отвечающие им трактовки кпд , и . Фор­мулы, определяющие в этих случаях величину упомянутых кпд, теорети­ческой скорости и связь последней с выбранным располагаемым перепа­дом, принимают следующий вид:

, ,

, ,

, .

При конкретных записях расчетных выражений мы будем использо­вать энергетическую и кинематическую формы их представления.

Рассмотрим энергетическую форму представления кпд. Для этого преобразуем формулу (3.2):

(3.4)

Располагаемые перепады и лопаточные КПД ступени Таблица 3.1

№ рис.	Параметры		Коэффициенты		Располагаемый перепад	Изоэнтропическая скорость	Лопаточный КПД
	Во входном сечении 0-0	В выходном сечении 2-2
3.1,а	В точке 0 статич-ие Р0, i0	В точке 2S статич-ое давл-ие Р2	0	0			по статическим параметрам перед и за ступенью
3.1,б	В точке 0* заторм-ые Р*0, i*0	В точке 2S статич-ое давл-ие Р2	1	0			по начальным параметрам тормож-ия и конечному стат-ому давлению
3.1,в	В точке 0* заторм-ые Р*0, i*0	В точке 2’* дав-ие тор-ия Р*2	1	1			по начальным и конечным парамет-ам торможения

Введем относительные величины потерь, отнесенные к располага­емым перепадам в ступени.

Например:

, , .

При использовании этих величин выражение (3.4) примет вид:

.

(3.5)

Используя общее определение лопаточного кпд (3.1) и выражения (3.5), легко получить формулы, представляющие различные трактовки этого кпд в энергетической форме:

(3.6)

Исходя из приведенного ранее выражения (1.8), мы можем пред­ставить три рассмотренные трактовки лопаточного кпд также в кине­матической форме в соответствии с трактовкой понятия располагаемого перепада:

(3.7)

Напомним, что выражения (3.6) и (3.7) отличаются лишь формой представления. В каждой из записанных групп формул трактовка кпд отвечает той, которая показана в последнем столбце табл.3.1.

Установим области рационального применения и взаимосвязь раз­личных трактовок понятия кпд.

Все трактовки понятия «лопаточный кпд», данные выше, одинаково правомочны, однако для объективного суждения об экономичности сту­пени каждую из этих трактовок рационально применять в зависимости от конкретных условий: трактовку - для ступеней, выходная скорость которых не используется (точнее - кинетическая энергия, соответствующая выходной скорости); - для ступеней, у кото­рых эта выходная скорость используется в проточной части за ними; - для ступеней, выходная скорость, в которых равна или близ­ка к входной скорости. В этом случае кпд близок по величине к , но применять его при тепловых расчетах групп ступеней удобнее.

Установим связь между , и . Напомним, что

, ,

,

,

.

Поэтому:

,

. (3.8)

Кроме того,

, (3.9)

. (3.10)

Одним из факторов, существенно влияющих на кпд турбинной сту­пени, является степень реактивности. Прежде чем говорить об этом влиянии, остановимся на зависимости степени реактивности от геомет­рических и режимных параметров ступени.

Запишем уравнение энергии (1.11) для контрольных сечений 0-0 и 1-1 соплового венца адиабатической ступени при изоэнтропическом течении:

.

Обозначим разность энтальпий (рис.3.2):

.

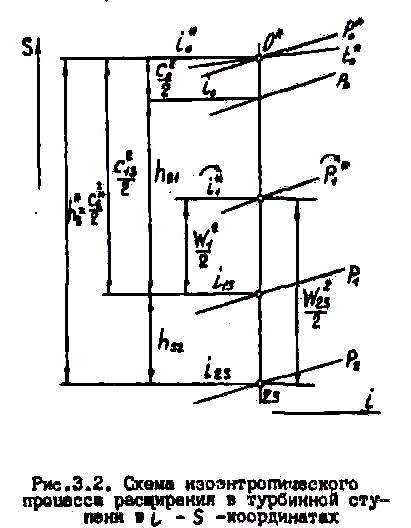
Эта разность является при­ращением кинетической энергии пара при его рас­ширении в сопловом венце. Ей соответствует конкрет­ное падение статического давления от Р₀ перед венцом до Р₁ за венцом. Аналогично, запись урав­нения энергии для контроль­ных сечений 1 и 2 рабочего венца в относительном дви­жении дает:

.

Величина называется реактивным перепадом на рабочем венце по статическим давлениям перед и за ним и характеризует увеличение кинетической энергии в рабочих лопатках.

Для соплового венца вместо перепада чаще используют величину .

Относительная величина реактивного перепада, как было сказано ранее, называется термодинамической степенью реактивности. Так как , а , то:

. (3.11)

Одним из основных геометрических параметров ступени, опреде­ляющих величину , является отношение площадей узких сечений каналов рабочих и направляющих лопаток . При одномерном течении в уплотненной ступени массовые расходы пара через рабочий и сопловой венцы равны: или, используя уравнение не­разрывности:

,

. (3.12)

Отношение зависит от и от отношения давле­ний . Если характеризовать последнее приведенной ско­ростью , то как показывают расчеты, при в зависимости от величины > 0 отношение < 1,1…1,15. Следовательно, в указанном диапазоне изме­нения , который соответствует большинству ступеней цилиндров высокого давления (ЦВД) и цилиндров среднего давления (ЦСД) современных конденсационных турбин, влияние сжимаемости не является решающим. Поэтому, пренебрегая для простоты этим влиянием, положим >0,97; и перепишем уравнение (3.12) так:

. (3.13)

Учитывая формулы (3.12) и (2.18)

,

.

Из треугольников скоростей (рис.1.4)

.

После преобразований получим из (3.13):

. (3.14)

На режимах работы турбинной ступени, мало отличающихся от расчетного, отношение меняется сравнительно мало. При учете этого обстоятельства оказывается, что выражение (3.14) при связывает отношение площадей и угол определяющие геометрию ступени «в главном», с режимными парамет­рами: и . При умеренных значениях влия­ние этого угла в выражении (3.14) не существенно.

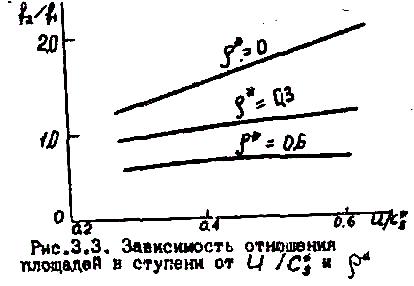
Для большей наглядности рассмотрим зависимость , построив соответствующие графики, приняв =16°, и не учитывая сжимаемость. Эти графики показаны на рис.3.3. Анализируя их, можно сделать следующие выводы:

- при фиксированном значении и заданной конструкции соп­лового аппарата ( =const) с уменьшением отношения сте­пень реактивности в сту­пени возрастает. Влияние на ее величину является решающим;

- при фиксированном значении степени реактивности отношение с увеличением отношения становится больше. Интенсивность роста отношения площадей максимальна при =0 и уменьшается по мере возрастания . Большим степеням реактивности соответствуют малые величины отношения и наоборот.

Следует отметить, что при таком подходе к рассмотрению вопроса каждому отношению соответствует своя ступень, а при фиксированном значении угла - свои профили рабочих лопаток. У кон­кретной ступени, работающей при переменных , отношение не меняется. Зависимость степени реактивности от для этого случая будет рассмотрена в последующих разделах курса.

Все сказанное выше о степени реактивности, включая и рассмотрение формулы (3.14), относилось к случаю, когда сжимаемость не оказывала влияния на работу ступени ( 0,97; ).

В общем случае с учетом сжимаемости и формулы (3.12)

,

где - отношение площадей, найденное без учета сжимаемости.

В результате рассмотрения вопроса о степени реактивности мы приходим к выводу, что при проектировании ступеней отношение есть функция от , , , . При работе ступени .

В дозвуковых ступенях при определяющей явля­ется связь ; ; .

В случае малых относительных высот лопаток (при больших отно­шениях , о влиянии которых на работу ступени в курсе будет сказано особо), обычно выдерживается соотношение: 1,1…1,15 и лишь при больших относительных высотах 1.

В соответствии с уравнением неразрывности

(3.15)

или при :

. (3.16)

Учитывая формулы (1.29) м (1.30), из выражений (3.15) и (3.16) имеем:

, то есть

Обозначим . Эта величина обычно лежит в пределах 0,9 < < 1,5.

Нижний предел относится к ступеням, срабатывающим малые перепады давлений при дозвуковых скоростях, верхний предел - к сверхзвуковым ступеням с большими перепадами давлений. Величина меняющаяся в указанных, сравнительно узких пределах, характеризует степень расширения рабочей среды в рабочих лопатках, скорректированную на отношение высот лопаток . Значения , , , , и полностью определяют треугольники скоростей и позволяют наглядно провести анализ влияния отдельных факторов на кпд ступени. Перейдем к этому анализу.