
- •Раздел 2
- •1.1. Основные уравнения одномерного движения
- •Уравнение состояния
- •Уравнение неразрывности
- •Уравнение количества движения
- •1.2. Газодинамические характеристики лопаточных венцов
- •1.3. Треугольники скоростей
- •Из рассмотренных треугольников скоростей вытекают следующие очевидные соотношения:
- •2. Тепловой расчет осевой турбинной ступени
- •2.1. Рабочий процесс в соплах, его построение в I - s – диаграмме и определение скоростей
- •2.2. Процесс в рабочих лопатках, его построение
- •2.3. Определение проходных площадей и высот облопачивания
- •3. Лопаточный коэффициент полезного действия
- •3.1. Вводные замечания и определения
- •3.2. Лопаточный кпд чисто осевой активной
- •Анализ формулы Банки
- •3.3. Лопаточный кпд турбинной ступени в общем случае
- •4. Ступени с колесами скорости
- •4.1. Назначение и устройство колес скорости
- •4.2. Рабочий процесс в колесах скорости
- •Основные характеристики ступеней
- •4.3. Некоторые практические данные по колесам скорости
- •Типовая комбинация кс-1а
- •5.1. Нерасчетные режимы работы одиночных ступеней
- •Ступени с малыми дозвуковыми скоростями
- •5.2. Нерасчетные режимы ступеней паровой турбины при работе их в составе отсека
- •Оглавление
1.3. Треугольники скоростей
Одним из наиболее распространенных способов расчета турбинной ступени по одномерной теории является расчет, в котором кинематика потока определяется путем построения треугольников скоростей.
При рассмотрении сложного абсолютного движения рабочей среды в проточной части ступени его разлагают на переносное и относительное движение. За абсолютное принимается движение в неподвижной системе координат, связанной с корпусом турбины. Переносное движение связано с равномерным вращением ротора n (об/с), вследствие которого рабочее тело в межлопаточных каналах рабочих лопаток переносится в окружном направлении с окружной скоростью u (число оборотов ротора составляет n=50 об/с или 3000 об/мин для стран с частотой тока в сети f=50 Гц). Относительным является движение рабочего тела по отношению к рабочим лопаткам (например, между сечениями 1 и 2 - движение вдоль межлопаточных каналов относительно поверхности лопаток).
Обозначим:
![]() - скорость рабочей среды в абсолютном
движении;
- скорость рабочей среды в абсолютном
движении;
![]() - скорость рабочей среды в относительном
движении;
- скорость рабочей среды в относительном
движении;
![]() - скорость переносного движения.
- скорость переносного движения.
Очевидно, что упомянутые составляющие скорости образуют векторный треугольник;
![]() .
(1.26)
.
(1.26)
Если
рассматривать движение в ступени,
используя систему координат:
z
- направление
оси вращения; r
- радиальное направление;
![]() -
направление по окружности, то скорость
рабочей
среды в общем случае может быть
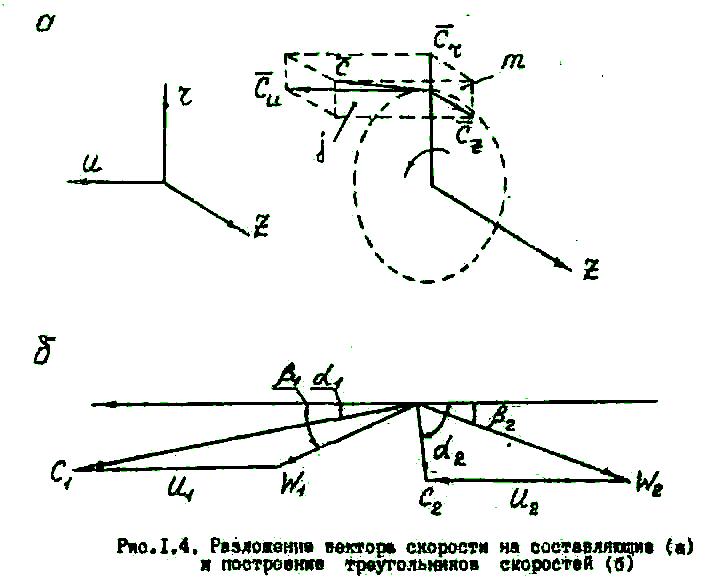
представлена, как на рис.1.4, а:
-
направление по окружности, то скорость
рабочей
среды в общем случае может быть
представлена, как на рис.1.4, а:
![]() (1.27)
(1.27)
Составляющие
![]() и
и
![]() лежат в плоскости, проходящей через
ось Z.
Эту плоскость мы в дальнейшем будем
называть меридиональной, обозначая
индексом m.
Плоскость, нормальную к меридиональной,
в которой лежат составляющие скорости
лежат в плоскости, проходящей через
ось Z.
Эту плоскость мы в дальнейшем будем
называть меридиональной, обозначая
индексом m.
Плоскость, нормальную к меридиональной,
в которой лежат составляющие скорости
![]() и
обозначим индексом j.
и
обозначим индексом j.
В
зависимости от вида ступени (осевая,
осерадиальная, радиальная) соотношения
между составляющими скорости
различны, равно как и соотношения между
проекциями ее на плоскостях m
и j.
Для рассматриваемого нами простейшего
случая осевой ступени при наличии в
ней радиального равновесия рабочей
среды радиальная составляющая скорости
![]() .
Поэтому проекция скорости
на плоскость m
равна
,
то есть
.
Поэтому проекция скорости
на плоскость m
равна
,
то есть
![]() ,
а вектор скорости
,
а вектор скорости
![]() (1.28)
(1.28)
вектор скорости лежит в плоскости j.
Учитывая
сказанное и то, чти вектор
лежит в плоскости j,
из (1.23) получаем
![]() .
.
Таким образом, для осевой ступени векторный треугольник скоростей, определяемый выражением (1.26), лежит в плоскости j. В дальнейшем мы будем опускать обозначения векторов при скоростях u, С и W.
В одномерной теории турбинной ступени в соответствии с формулами (1.26) и (1.28) строятся треугольники скоростей для контрольных сечений 1-1 и 2-2. Для удобства их часто совмещают на одном чертеже (рис.1.4, б).
Треугольник скоростей, относящийся к контрольному сечению 1-1, является входным для рабочих лопаток и выходным для сопловых. Треугольник скоростей, построенный для сечения 2-2, является выходным для рабочих лопаток.
При построении треугольников скоростей принято использовать следующие обозначения (см. рис.1.4, б):
![]() -
абсолютная скорость в сечении 1-1 выхода
потока из сопловых лопаток, входа потока
на рабочие лопатки;
-
абсолютная скорость в сечении 1-1 выхода
потока из сопловых лопаток, входа потока
на рабочие лопатки;
- средний угол между направлением потока в сечений 1-1 в абсолютном движении и направлением окружной скорости;
![]() -
относительная скорость в сечении 1-1
входа потока на рабочие лопатки;
-
относительная скорость в сечении 1-1
входа потока на рабочие лопатки;
- средний угол между направлением потока в сечении 1-1 в относительном движении и направлением окружной скорости;
![]() -
абсолютная скорость в сечении 2-2 выхода
потока из рабочих лопаток, а также
входа потока на сопловые лопатки
следующей ступени;
-
абсолютная скорость в сечении 2-2 выхода
потока из рабочих лопаток, а также
входа потока на сопловые лопатки
следующей ступени;
![]() -
средний угол между направлением потока
в сечении 2-2 в абсолютном движении и
отрицательным направлением окружной
скорости;
-
средний угол между направлением потока
в сечении 2-2 в абсолютном движении и
отрицательным направлением окружной
скорости;
- средний угол между направлением потока в сечении 2-2 в относительном движении и отрицательным направлением окружной скорости;
![]() -
относительная скорость в сечении 2-2
выхода потока из рабочих лопаток.
-
относительная скорость в сечении 2-2
выхода потока из рабочих лопаток.
В
осевой ступени величина окружной
скорости во входном и выходном
треугольниках скоростей одинакова:
![]() .
Отметим здесь, что в общем виде
.
Отметим здесь, что в общем виде
![]() ,
откуда видно, что если D1=D2,
то и
.
В действительности окружные скорости
равны по величине на среднем диаметре
при законе изменения меридионального
сечения DСР=const,
а при других (например, DКОР=const
или DПЕР=const)
обычно принимают, что окружные скорости
на среднем диаметре приближенно равны
,
откуда видно, что если D1=D2,
то и
.
В действительности окружные скорости
равны по величине на среднем диаметре
при законе изменения меридионального
сечения DСР=const,
а при других (например, DКОР=const
или DПЕР=const)
обычно принимают, что окружные скорости
на среднем диаметре приближенно равны
![]() .
.
Выражение
для окружной скорости показывает, что
ее величина увеличивается от корня
(корневого диаметра) лопаточного венца
к периферии (периферийного диаметра)
![]() ,
так как
,
так как
![]() .
.
В
учебной литературе используется единая
система отсчета углов
![]() и
и
![]() от положительного направления оси u.
В заводских методиках расчета
(например, на ЛМЗ) принята раздельная
система отсчета этих углов, которая
далее сохраняется как основная.
от положительного направления оси u.
В заводских методиках расчета
(например, на ЛМЗ) принята раздельная
система отсчета этих углов, которая
далее сохраняется как основная.
Во входном треугольнике скоростей углы и , отсчитываются против часовой стрелки от направления u. В выходном треугольнике скоростей углы и отсчитываются по часовой стрелке от направления -u.
