1.2. Газодинамические характеристики лопаточных венцов

Проточная часть турбинной ступени формируется из соплового (неподвижного) и рабочего (подвижного) лопаточных венцов. Их газо­динамические характеристики зависят от соотношений основных гео­метрических разметов (рис.1.2). В меридиональном сечении это длина (высота) лопатки , диаметр D, ширина лопаточного венца В; в цилиндрическом сечении - хорда профиля , угол установки про­филя в решетке ; шаг решетки - t, минимальное сечение О («горло») межлопаточного канала. Подстрочными индексами 1 и 2 будем обозна­чать контрольные сечения на выходе из соплового и рабочего венцов соответственно. В рамках одномерной теории ограничимся цилиндричес­ким сечением и плоской решеткой, относящимся к среднему диаметру ступени , где D_кор - корневой диа­метр.

Важными геометрическими показателями венцов являются отноше­ния и . Для плоской решетки при фиксирован­ном угле - относительный шаг и так называемый эффективный угол выхода потока ; . Для профиля в плоской решетке, имеющего заданную форму, эффективные углы однозначно связаны с углом и :

.

Влияние геометрических факторов на газодинамические характерис­тики венца в целом зависит от режимных параметров потока. Последние принято представлять в виде чисел подобия.

Для сжимаемой, вязкой, гомогенной рабочей среды при установившемся течении и малом влиянии массовых сил в их перечень входят:

числа М и Re, (соответственно – Маха и Рейнольдса), определяемые по скорости выхода потока из венца; угол входа потока на решетку ; степень турбулентности потока, а также показатели его неоднородности перед решеткой.

При сверхзвуковых течениях к названным величинам следует доба­вить показатель адиабаты к, при течении влажного пара - степень сухости X и другие.

Иными словами, состав режимных параметров потока определяется условиями задачи, которая подлежит решению. В функции названных параметров, как результат экспериментальных исследований, находятся газодинамические характеристики соплового и рабочего лопаточных венцов. Основными из них являются: коэффициент расхода (для соплового венца); (для рабочего венца); коэффициент потерь энергии ₁, ₂; угол выхода потока из венца ₁, ₂.

Коэффициент расхода представляет отношение действительного расхода G рабочей среды через венец к теорети­ческому G_s, соответствующему идеальному (изоэнтропическому) про­цессу истечения. Обычно принимают, что в таком процессе давление за решеткой равно среднему давлению в действительном процессе

,

а угол выхода потока из решетки совпадает с осредненным по шагу углом выхода в действительном процессе.

Теоретический расход G_S может быть определен исходя из урав­нения (1.6). Например, для соплового венца

, (1.16)

где C_1S и _1S - скорость и плотность в потоке на выходе из решет­ки при теоретическом процессе; f₁ - суммарная площадь узких се­чений межлопаточных каналов ( ).

Таким образом, можно записать для соплового венца , для рабочего - .

В ряде случаев удобно представление расхода G_1S c использо­ванием приведенной плотности потока массы :

. (1.17)

При критическом истечении в узком сечении сужающейся решетки параметры С_1S , _1S равны критическим, а =1.

Коэффициент потерь энергии представ­ляет собой отношение части кинетической энергии потока, затраченной в межлопаточных каналах на преодоление сил сопротивления и необра­тимо превратившейся в тепло, к располагаемой кинетической энергии.

За располагаемую энергию принимается кинетическая энергия потока при изоэнтропическом процессе истечения.

Запишем уравнение энергии (1.13) для истечения из соплового венца реального потока и для случая изоэнтропического истечения .

Разность кинетических энергий изоэнтропического и реального потоков является потерей механической энергии, необратимо превра­тившейся в теплоту:

. (1.18)

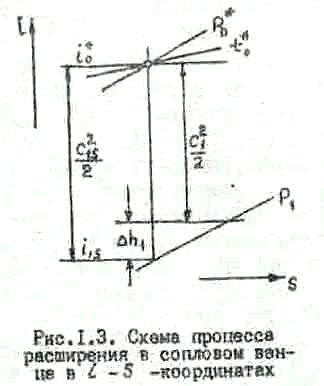
Условно полагаем, что теплота нагревает рабочую среду при Р₁=const (рис.1.3). В соответствии c данным определением коэффициент потерь соплового венца определится как

. (1.19)

Аналогично, для рабочего венца:

. (1.20)

Исходя из выражений (1.19) и (1.20) вводят понятие коэффициентов скорости соплового венца и ра­бочего венца :

, , (1.21)

, , (1.22)

Как и коэффициенты потерь, коэффициенты скорости - результат осреднения скорости исходя из уравнения энергии.

Потери механической энергии в лопаточных венцах - следствие достаточно сложного комплекса явлений. Эти потери можно разделить на несколько составляющих. Наиболее изученными из них являются:

- профильные потери, величина которых характеризуется коэф­фициентом ;

- концевые потери, определяемые коэффициентом ;

- потери от нестационарности обтекания венца, характеризуемые коэффициентом .

Названные составляющие коэффициента потерь определяются на основе экспериментальных исследований плоских и прямых решеток профилей, а также исследований облопачивания в кольцевых решетках и экспериментальных турбинах.

Коэффициент потерь лопаточного венца, используемый в одномер­ном расчете, представляется в виде суммы:

. (1.23)

В общем случае для произвольных решеток рабочих и направляющих лопаток каждая из названных составляющих потерь является функцией от геометрических ( , в, , , ) и газодинамических ( , , , , , Re) параметров, определяющих поток в решетке. Для разных решеток эти функции различны.

В процессе проектирования ступеней форма профилей и параметры решеток, как правило, уточняются. В этих условиях расчет приходится вести методом последовательных приближений, корректируя значение по мере уточнения информации о решетках.

До выбора конкретных решеток профилей (на стации эскизного проектирования) ориентируются на обобщенные статистическими мето­дами результаты экспериментальных исследований решеток профилей – обобщенные зависимости. Для возможности тепловых расчетов нами бу­дет использоваться следующее аналитическое представление таких зависимостей необратимых потерь энергии в решетках:

(1.24)

Здесь и - углы входа и выхода потока из решетки, выраженные в радианах. Коэффициент учитывает рост потерь энергии в ступени по сравнению с вычисленными по данным стати­ческих исследований, вызванный нестационарностью потока в ступени.

При использовании обобщенных зависимостей вида (1.24) отпа­дает необходимость в предварительном выборе профилей сопловых и рабо­чих лопаток. Однако после выбора решеток необходимо выполнить по­верочные расчеты с учетом действительных параметров облопачивания.

Угол выхода потока из венца - осредненная величина угла между вектором скорости и фронтом лопаточной решетки, определяемая на основе данных ее экспериментальных исследований. Осреднение производится по шагу t и высоте лопаток на основе уравнения количества движения. Так для соплового венца

. (1.25)

Аналогично для рабочих лопаток определяется .

Осредненные значения углов выхода потока из плоских решеток близки к значениям соответствующих эффективных углов:

, .

Приближенная аналитическая связь этих углов показана в монографии [4].

Под газодинамическими характеристиками лопаточных венцов да­лее подразумеваются экспериментальные зависимости коэффициентов расхода , ; коэффициентов потерь , ; углов выхода потока , от перечисленных выше геометрических и режимных параметров, определяющих течение в венце. Об этом подробнее можно посмотреть в работе [3].