3.3. Лопаточный кпд турбинной ступени в общем случае

Ступени с , но при

К подобным ступеням относятся не только осевые, но также и чисто радиальные (рис. 3.10), если отношение мало отлича­ется от единицы:

0,95…1,05.

Заметим, что в общем случае отношение , характери­зующее степень радиальности течения, является определяющим пара­метром. При одномерной постановке задачи в случае осевых ступеней оно, так же как отношение , не влияет на решение. Для радиально-осевых и радиальных ступеней не учитывать его нельзя.

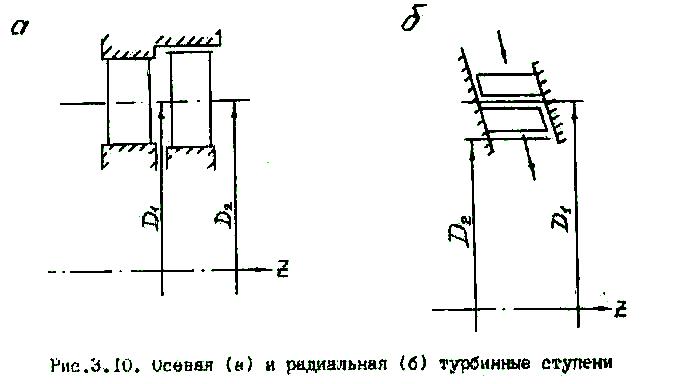
Для определения кпд ступени при произвольной степени реактив­ности может быть выведена общая формула, подобно тому, как была получена формула Банки. Однако для анализа работы ступени более наглядным является расчет по треугольникам скоростей. Как отмечено выше (см. разд.3.1), при рассмотрении взаимосвязи степени реактив­ности , отношения и отношения площадей , треугольники скоростей полностью определяются значениями , , , , и .

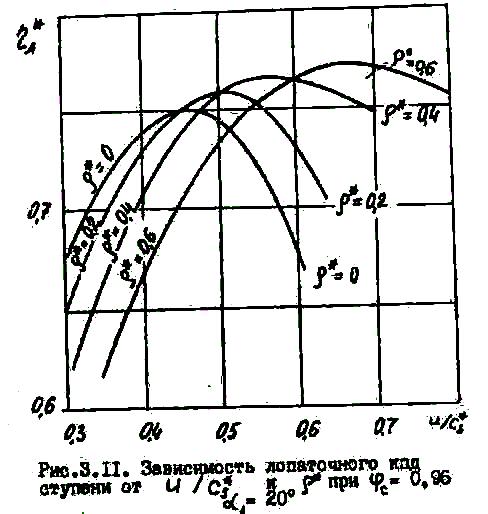
На рис.3.11 представлены графики зависимостей = ( )_^*_=сonst, которые построены для разных по данным такого расчета на ЭВМ при значениях и , определенных по геометри­ческим параметрам ступеней ЦВД, и приведенным в разд.1.2 обобщенным зависимостям для профильных и концевых потерь (1.24).

Из этих графиков видно:

- параболичес­кий характер зави­симости = ( ) сохраняется и в об­щем случае;

- величина слабо влияет на аб­солютное значение ( )_max, которое несколько возраста­ет с увеличением ;

- значение ( )_опт, при котором достигается значение ( )_max, становится больше по мере увеличения .

При >0, как и в случае =0, ( )_опт лишь незначительно превышает значение ( )_.

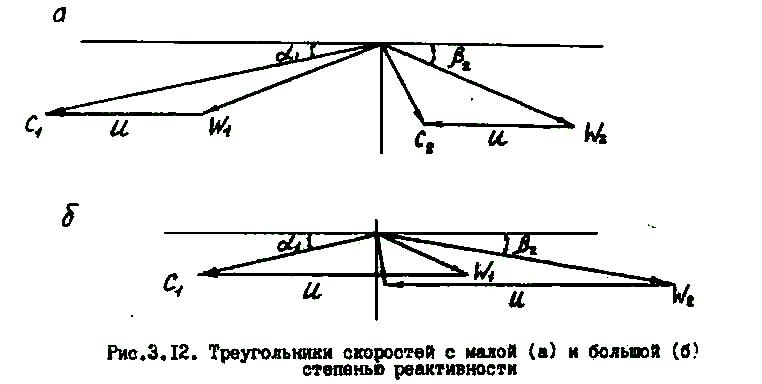
Поэтому для объяснения роста ( )_опт с увеличением мож­но рассматривать условие сохранения осевого выхода потока. На рис.З.12 показаны треугольники скоростей, построенные для малого и большого значений степени реактивности при одинаковых и .

В случае большой скорость больше, а угол мень­ше, чем при малой . Поэтому для того, чтобы выход из ступени был осевым, при большой степени реактивности требуется большая окружная скорость и, следовательно, большее значение .

Здесь мы полагаем, что , , хотя, конечно, тот же результат был бы, если принять, что , . Для выбора ( )_опт в зависимости от может быть ис­пользована следующая приближенная формула:

.

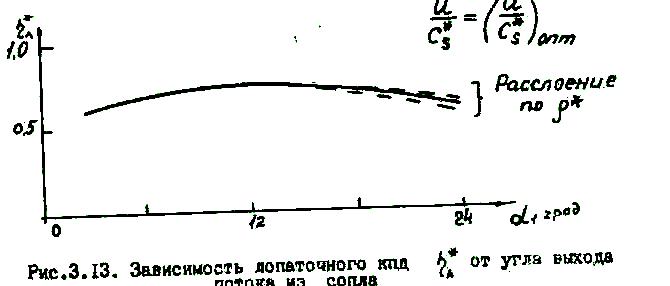
Для ступеней, работающих без использования выходной скорости, зависимость = ( ) аналогична той, которая проявлялась в формуле Банки. Как видно из рис.3.13, оптимальное значение , соответствующее = , имеет порядок . Падение при меньших вызывается увеличением потерь энергии в соплах и в рабочих лопатках; при больших - увеличением по­терь с выходной скоростью; при  12° начинается расслоение графиков = ( ) по величинам степени реактивности .

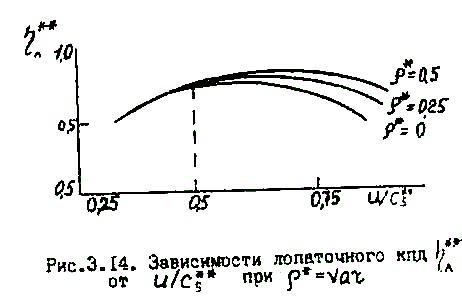
По аналогии с тем, как было сделано для чисто активной ступени, исходя из выражений (3.10) и (3.8) на рис.3.14 представлены зависимости = ( ; ).

Из графиков следует:

- примерно до =0,5 влия­ние степени реактивности на кпд почти не сказывается;

- при больших вплоть до 0,8 кпд меняется слабо:

.

В диапазоне =0…0,5 0,6…0,8. В заводской практике обычно используют меньшие значения , при которых примерно совпадает с направлением осевого выхода.

Ступени, выходная скорость рабочей среды из которых меняется с изменением режима работы, имеют увеличенный кпд , особенно в тех областях изменения , где велики потери с выходной скоростью. Поэтому большие степени реактивности применяются в сту­пенях, которые могут работать при переменных .

Еще раз подчеркнем, что кпд рационален для ступеней, вы­ходная скорость которых не используется, кпд - для ступеней, работающих в группе с использованием выходной скорости.

Следует различать физический смысл характерных величин при построении зависимости = ( ):

- значение , при котором вектор скорости ;

- значение , при котором имеет место максимум кпд ;

- оптимальное значение соответствующее максимуму кпд .

Очевидно, величина , является оптимальной для ступеней, работающих в группе.

Заметим, что вопрос о выборе технико-экономического значения , отличающегося в принципе от , будет рассмотрен далее, при изложении материалов об отсеках ступеней.

Для ступеней, работающих с использованием выходной скорости и , значение , как видно на рис.3.15, увеличено по сравнению с его значением для одиночной ступени. Соответственно, > во всем представленном диапазоне изменения .

В первом приближении можно считать, что +(3…6)%.

Ступень с и (радиально - осевая ступень)

До сих пор нами рассматривались чисто осевые ступени, средние диаметры которых перед рабочим венцом и за ним были одинаковы и поэтому окружные скорости в этих сечениях были равны: .

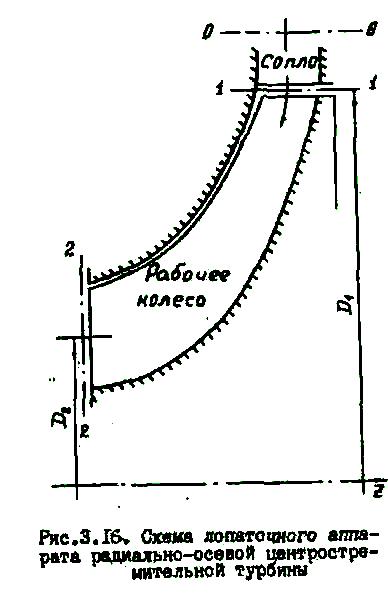
В турбиностроении широко применяются турбинные ступени другого типа, в рабочих колесах которых течение является осерадиальным (се­чение лопаточного канала в меридиональной плоскости представлено на рис.3.16). Для подобных неосевых ступеней отношение , существенно отличается от единицы, а окружные скорости и - друг от друга.

Не останавливаясь на выводах аналитических выра­жений, определяющих зависи­мости кпд и в функ­ции геометрических и режим­ных параметров, рассмотрим лишь физические стороны ра­бочего процесса радиально-осевой ступени.

Для радиально-осевой ступени относительная ско­рость выхода потока из ра­бочего венца при изоэнтропическом процессе

. (3.21)

Радиально-осевая сту­пень может быть центробежной (рабочее тело удаляется от оси вращения) и центростре­мительной (рабочее тело дви­жется от периферии к оси вра­щения). При прочих равных условиях, как видно из формулы (3.21), работа кориолисовых сил, определяемая разностью , в центробежной ступени приводи к увеличению, а в центростремитель­ной - к уменьшению скорости по сравнению с осевой ступенью.­

Это значит, что

- уровень относительных скоростей в центростремительной ступе­ни будет значительно меньше, чем в центробежной, в связи с чем, в первую очередь, кпд центростремительной ступени оказывается выше, чем центробежной;

- при одинаковых окружных скоростях в центростремительной ступени реализуется больший изоэнтропический перепад энтальпий, чем в центробежной.

Отмеченные положительные качества обуславливают преимущест­венное применение центростремительных ступеней, например, в приво­дах вспомогательных механизмов, в газовых турбинах малой мощности, турбодетандерах и т.п. Однако область применения центростремительных турбин ограничена трудностями использования их при больших объемных расходах рабочей среды даже в двухпоточных радиадьно-осевых ступенях. В стационарных ПТУ нашли применение центробежные ступени и турбины, турбины типа «Юнгстрем», центростремительные типа «Сименс».

Возвращаясь к формуле (3.21), следует отметить, что ее подко­ренное выражение не может быть отрицательным, так как >0. Необходима проверка внутреннего контура ступени с тем, чтобы это условие выполнялось во всех его цилиндрических сечениях. В случае нарушения условия >0, например, с изменением числа, оборотов ротора, в части рабочего колеса возникают обратные токи, и ступень становится неработоспособной. 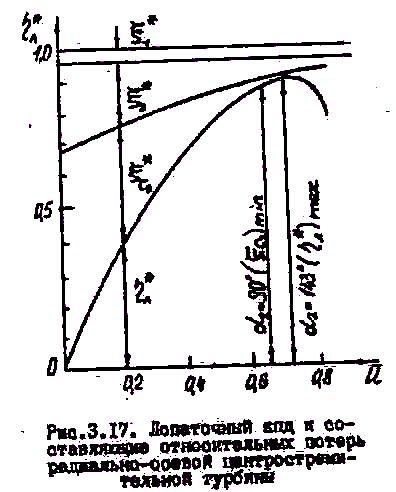При конкретных это условие ограничивает ступени, что видно из зависимости = ( ), представленной на рис.3.17 . Так же показано изменение отдельных составляющих потерь в ступени в функции . В рассматриваемом конкретном примере =0,82. Если может возрастать до величены , то стремится к нулю, поскольку и также стремится к нулю, однако на таких режимах работа ступени становится невозможной. Максимальное значе­ние = достигается при < , 0 и 90^.

Как показали расчеты, при одинаковых углах , и коэффици­ентах для центростремительной ступени с = 0,5 и =0,85 величины меньше на 10-15% (относительных), а вдвое меньше, чем для осевой ступени с = 0,95.

Напомним, что на зависимости, представленной на рис.3.17, каждому значению соот­ветствует своя ступень. Для ориентировочных оценок оптимальных значений и можно использовать выражения, приведенные ниже:

,

.

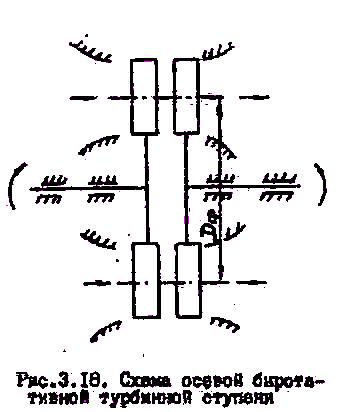
Биротативные ступени (ступени двойного вращения)

В подобных ступенях оба венца закреплены на разных валах и вращаются в разные стороны (рис.3.18). Обычно при этом их окружные скорости равны по величине и противоположно направлены по направлению: .

Для анализа работы биротативной ступени можно представить ее в виде некоторой фиктивной ступени, в которой один венец неподвижен, а второй вращается относительно первого с некоторой скоростью .

При таком подходе можно все выводы сделанные для ступени одинарного вращения, отнести к комплексу двух смежных венцов, вращающихся в разные стороны.

Если на каждом из венцов «срабатываются» одинаковые перепады и =0,5, то, используя понятие об оптимальном значении осевой ступени, найдем для такой биротативной ступени:

,

то есть:

.

Биротативной Ступени одинарного

ступени вращения (осевой)

Таким образом, оптимальное значение биротативной ступени вдвое меньше, чем у обычной осевой ступени. Это значит, что при одинаковых окружных скоростях и оптимальном отношении располагаемый перепад в биротативной ступени будет в четыре раза большем, чем в осевой ступени, имеющей неподвижный сопловой венец. При этом из-за отсутствия последнего и, следовательно, отсутствия потерь в нем, кпд биротативной ступени оказывается выше, чем у осевой.

Удачным примером использования биротативных ступеней является центробежная турбина Юнгстрема, однако, мощности подобных машин ограничены условиями прочности.