Потери напора по длине турбулентного потока.График Никурадзе

Получить закон распределения местных скоростей по сечению турбулентного потока теоретически не представляется возможным,поскольку скорости в каждой точке изменяются по величине и направлению.

Изменения компоненты истинной мгновенной скорости w_мвдоль оси потока для некоторой точки в зависимости от времени представлены на графике,из которого видно, что компоненты истинных локальных скоростей пульсируют около некоторого осредненного (среднего по времени) значения . Разница между истинной и осредненной скоростью называется пульсационной скоростью ∆ .

υ_м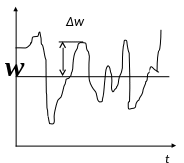

Характеристики турбулентности.

1. Интенсивность турбулентностиI_T:

где - среднее квадратичное значение ( = ) пульсационной скорости. Обычно при движении по трубам

I_T=0,01 ÷ 0,1.

2. Масштаб турбулентности – ℓ _T

Масштаб турбулентности, называемый также путем смещения, представляет собой расстояние, которое проходит совокупность жидких частиц (вихрь) в поперечном направлении потока с момента возникновения до взаимодействия с другим вихрем, то есть до разрушения. По мнению ряда исследователей, эта величина идентична по своему смыслу пути свободного пробега молекулы в молекулярно-кинетической теории газов, т.е. и в этом случае предполагается, что движение вихря в потоке ограничено пространством аналогичного поведения другого вихря.

3. Турбулентная вязкость – μ_Т

Согласно закону вязкого трения касательное напряжение при ламинарном режиме одномерного течения определяется:

Здесь μ – коэффициент динамической вязкости (является физической константой), – изменение местной скорости вдоль оси, перпендикулярной направлению потока.

Напряжение вязкостного трения обусловлено силами взаимодействия между молекулами жидкости. В отличие от ламинарного, при турбулентном режиме движения макроскопические частицы жидкости существенно перемещаются не только в продольном, но и в поперечном направлении потока, увеличивая касательное напряжение. По аналогии с вязкостным трением Буссинеском предложено выражение для дополнительной (турбулентной) составляющей полного касательного напряжения:

гдеμ_Т – коэффициент турбулентной вязкости. Коэффициент турбулентной вязкости не является физической константой, а зависит от абсолютной величины и степени неоднородности скорости потока, интенсивности и масштаба турбулентности. Таким образом, полное касательное напряжение в турбулентном потоке есть сумма:

У стенки, в вязком подслое, движение ламинарное, и, следовательно, нет дополнительных касательных напряжений, а в турбулентной области основную роль играет турбулентная вязкость.

Согласно полуэмпирической теории Прандтля,

, причем ℓ_T= k · z,

где k – универсальная постоянная турбулентного потока.

Предполагается, что полное касательное напряжение в пристенной области (вязком подслое) турбулентного потока есть величина постоянная, поэтому для τ по всему сечению потока можно записать:

Распределение местных скоростей по сечению турбулентного потока.

Из предыдущей формулы следует, что

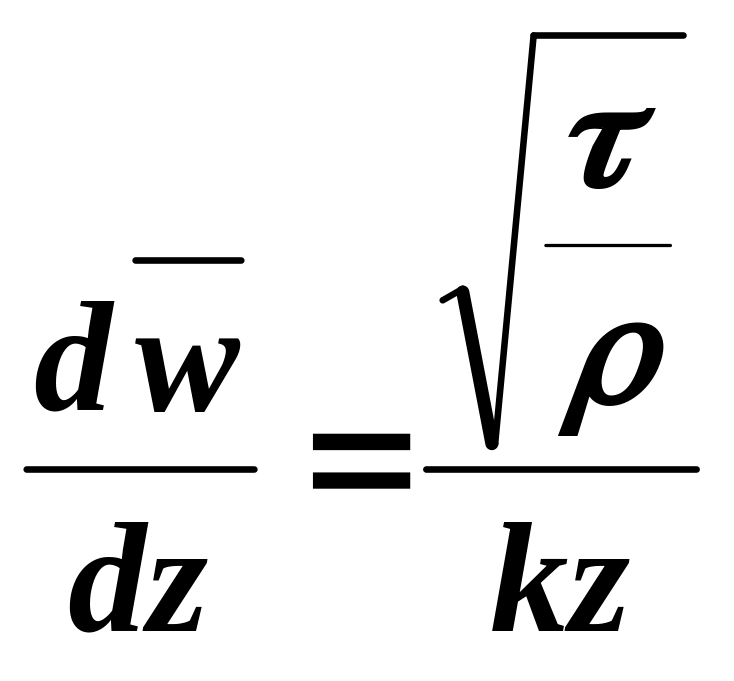
После разделения переменных и интегрирования получаем:

→ ,

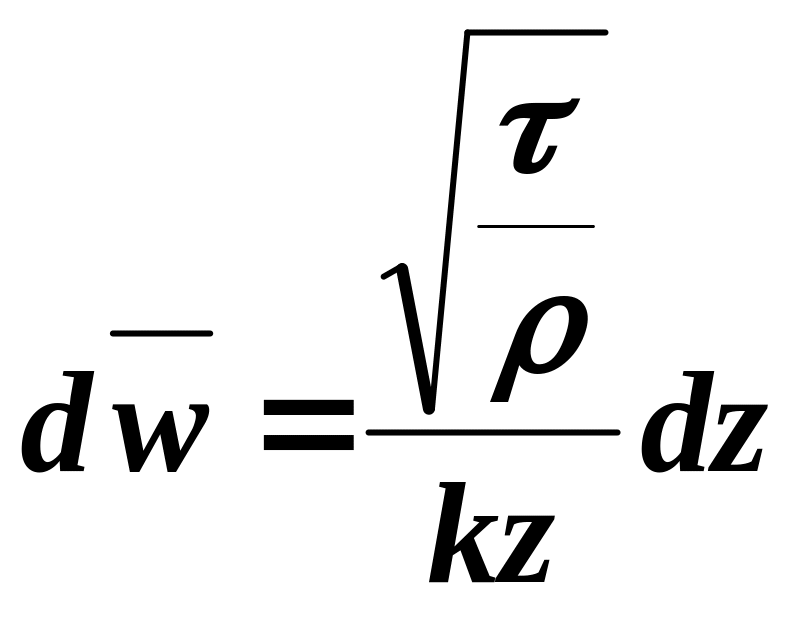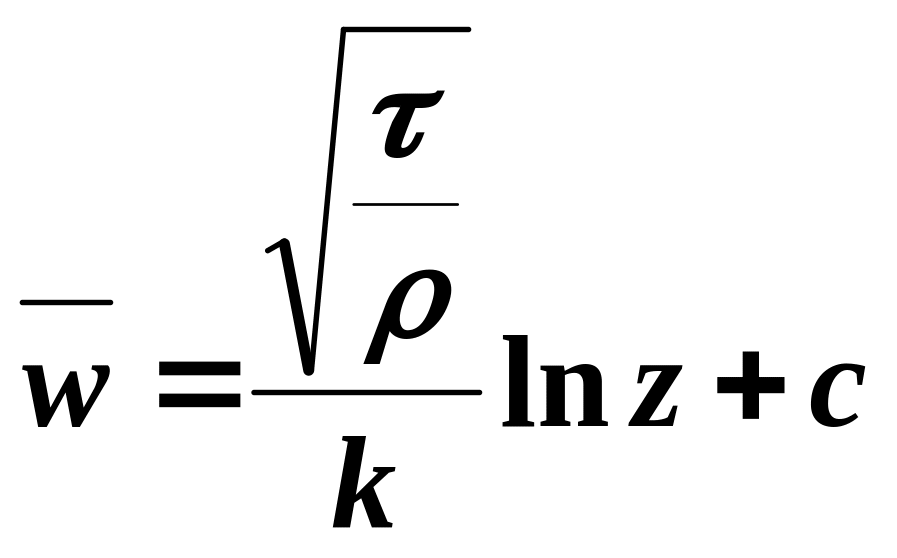И если обозначить как динамическую скорость υ_* , то

Как видно из полученного уравнения, осредненная скорость изменяется по сечению в турбулентной области по логарифмическому закону. Опыты показали, что указанное уравнение при определенных условиях может быть распространено на весь турбулентный поток. Однако в инженерных расчетах удобнее обращаться к формуле Дарси-Вейсбаха, а для определения величины λ использовать экспериментальные данные (график Никурадзе или эмпирические уравнения).