Гидромеханические процессы и аппараты

Прикладная гидромеханика Гидростатика. Основное уравнение гидростатики. Сила давления жидкости на стенки сосудов (плоские и криволинейные поверхности).

Гидродинамика. Классификация жидкостей. Виды движения жидкости. Поток жидкости и его геометрические элементы и гидравлические параметры. Уравнение Бернулли для потока вязкой жидкости. Гидравлическое сопротивление аппаратов и трубопроводов. Сопротивление круглых трубопроводов по длине. Формулы Пуазейля и Дарси-Вейсбаха. График Никурадзе. Движение жидкости в некруглых трубах. Местные гидравлические сопротивления. Расчет простых и сложных трубопроводов. Определение оптимального диаметра трубопровода. Особенности течения газа.

При расчетах процессов и аппаратов химических технологий необходимо учитывать гидродинамические условия в аппаратах.

Основное уравнение гидростатики

В гидростатике изучают равновесие жидкостей, находящихся в состоянии относительного покоя. ( При этом форма объема жидкости не меняется, а силы внутреннего трения отсутствуют ).

В любой покоящейся жидкости . Уравнения Навье-Стокса переходят в уравнения Эйлера:

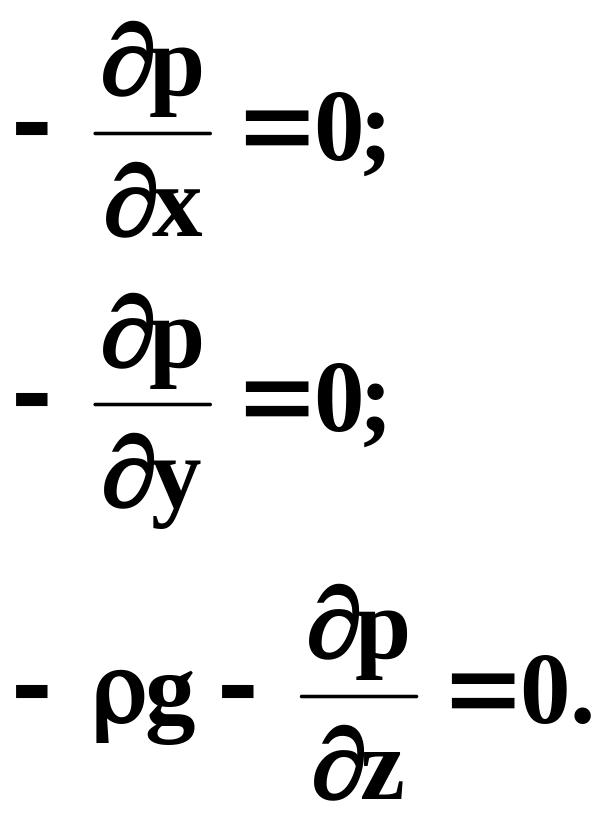
Из уравнений Эйлера следует, что давление в покоящейся жидкости изменяется только по координате z и постоянно во всех точках горизонтальной плоскости, так как

Интегралом уравнений Эйлера является основное уравнение гидростатики.

(*) ;

z- геометрический напор; ( характеризует удельную потенциальную энергию положения данной точки на произвольно выбранной плоскости ),

- гидростатический (пьезометрический) напор (характеризует удельную потенциальную энергию давления в данной точке).

Для двух произвольных горизонтальных плоскостей І-І и ІІ-ІІ уравнение (*)приобретает вид:

(**)

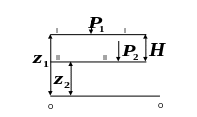
Решим (**) относительно P₂

- Это уравнение - 3акон Паскаля– Давление, создаваемое в любой точке покоящейся несжимаемой жидкости передается во все стороны с одинаковой силой.

Основное уравнение гидростатики (3акон Паскаля)–применяют для расчета давления на дно и стенки сосудов, гидростатических машин, гидрозатворов, и др.

Давление покоящейся жидкости на дно и стенки сосуда

Давление жидкости на горизонтальное дно сосуда везде одинаково. Давление же на его боковые стенки растет с увеличением глубины. Давление на дно не зависит от формы или угла наклона боковых стенок сосуда, а также от объема жидкости в нем.

( p₁- давление на поверхности жидкости, p₂- давление на дно сосуда ).

То есть p₂ зависит только от H – столба жидкости.

Общая сила давленияP=pF или ; - площадь дна сосуда.

Сила давления на вертикальную стенку:

где: h-расстояние от верхнего уровня жидкости до центра тяжести смоченной площади . Сила давления на вертикальную стенку равно произведению ее смоченной площади на гидростатическое давление в центре тяжести смоченной площади стенки. Точка приложения сил давления на стенку называется центром давления.

Уравнение Бернулли

Интегрирование дифференциальных уравнений движения Эйлера приводит к важнейшему уравнению гидродинамики - уравнению Бернулли. Это уравнение широко используется в инженерных расчетах.

- уравнение Бернулли для идеальной жидкости.

z- нивелирная высота ( геометрический напор )

- гидростатический напор;

- динамический напор;

Из уравнения Бернулли - для любого сечения потока сумма потенциальной и кинетической энергий жидкости - величина постоянная.

( Уравнение Бернулли – это частный случай закона сохранения энергии). При движении реальной жидкости гидродинамический напор H не остается постоянным, так как частицы жидкости встречают сопротивление, вызванное силами вязкости и различными другими препятствиями.

На преодоление этого сопротивления, которое называется гидравлическим, расходуется энергия движущейся жидкости, которая превращается в тепло. Это тепло рассеивается в окружающую среду.

Следовательно: .

Чтобы сохранить равенство напоров в любом сечении потока в правую часть уравнения Бернулли следует добавить член, учитывающий потерю напора:

- потери напора на трение, - потери напора на преодоление местных сопротивлений ( повороты, расширения, вентили, краны и т.д.)

С помощью уравнения Бернулли можно определить необходимый напор для того, чтобы жидкость транспортировалась по данному каналу с заданной скоростью.