МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Ижевский государственный технический университет
им. М.Т. Калашникова»
Кафедра «Вычислительная Техника»
Отчет по лабораторной работе №1
по дисциплине «Теория принятия решений»
Выполнил:
студент группы 6-78-3
Симонов М.В.
Принял:
к.т.н., доцент
Коробейникова Ирина Вячеславовна
Ижевск 2013
Задача 1.
Задача 2.
Порядок выполнения:
Решение первой задачи минимизации (максимизации) графическим методом.
Решение первой задачи минимизации (максимизации) симплекс методом.
Составление двойственных задач линейного программирования для первой задачи и решение их симплекс-методом.
Решение второй задачи симплекс методом.
Составление двойственной задачи линейного программирования для второй задачи и решение её симплекс-методом.
Ход работы
Решение первой задачи минимизации (максимизации) графическим методом.
Для решения задачи графическим методом, построим прямые ограничения, а также поверхность целевой функции L. Для этого найдем точки пересечения с осями Оx1 и Ox2 для каждой прямой ограничения.
5x1-2x2=0 |
|
|
x1+x2=1 |
|
|
|
x1 |
0 |
0,6 |
|
x1 |
0 |
1 |
x2 |
-1,5 |
0 |
|
x2 |
1 |
0 |
|
|
|
|
|
|
|
-3x1+x2=3 |
|
|
2x1+x2=4 |
|
||
x1 |
0 |
-1 |
|
x1 |
0 |
2 |
x2 |
3 |
0 |
|
x2 |
4 |
0 |
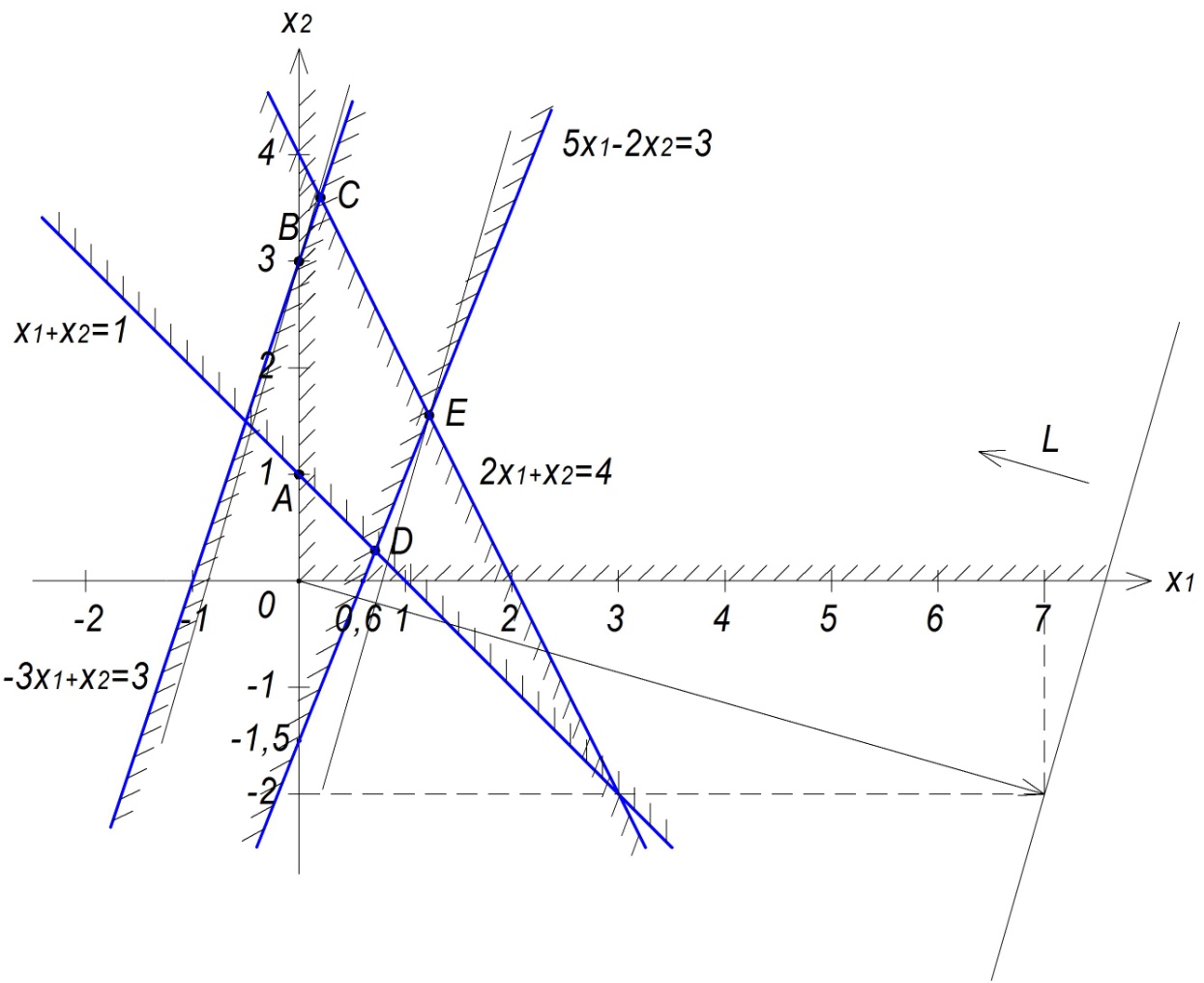
В результате получилась ограниченная область ADECB. Определим координаты этих точек.
Точка A:
x1=0, x2=1
Точка D:
Для определения координаты этой точки решим систему уравнений, состоящую из уравнений x1+x2=0 и 5x1-2x2=3.
x1=1-x2
5(1-x2)-2x2=3
5-5x2-2x2=3
7x2=2, x2=2/7
x1=1-2/7, x1=5/7
Точка E:
Для определения координаты этой точки решим систему уравнений, состоящую из уравнений 2x1+x2=4 и 5x1-2x2=3.
x2=4-2x1
5x1-2(4-2x1)=3
5x1-8+4x1=3
x1=11
x2=4-22, x2=-17
Точка C:
Для определения координаты этой точки решим систему уравнений, состоящую из уравнений 2x1+x2=4 и -3x1+x2=3.
x2=4-2x1
5x1-2(4-2x1)=3
5x1-8+4x1=3
9x1=11, x1=11/9
x2=4-22/9, x2=14/9
Точка B:
x1=0, x2=3
Наибольшее значение функция будет принимать в точке E(11/9,14/9), где x1=11/9, x2=14/9. L=7(11/9)-2(14/9)=49/9 – наибольшее значение функции.
Наименьшее значение функция будет принимать в точке B(0,3), где x1=0, x2=3. L=7(0)-2(3)=-6 – наименьшее значение функции.
2. Решение первой задачи минимизации (максимизации)симплекс методом
Необходимо найти начальное опорное решение для целевой функции L, которое бы удовлетворяло системе наложенных ограничений.
Запишем первую задачу в канонической форме, чтобы все условия системы представляют собой уравнения. Чтобы уравнять неравенства нужно добавить в каждое из них (или вычесть из каждого) по одной неотрицательной переменной - s1, s2, s3, s4 (соответственно в каждое их неравенств).
В неравенство
,
и
мы добавим переменную s1,
s3, s4
соответственно, а из неравенства
вычтем
неотрицательную переменную s2,
так как в нем установлен знак 
Каноническая форма задачи:
Определимся с начальным опорным решением.
Наличие единичного базиса позволяет
найти опорное решение. В уравнении
нет переменной, которая бы входила в
данное уравнение с коэффициентом 1, а в
остальные уравнения системы с коэффициентом
0. Поэтому добавим в уравнение
искусственную переменную r1.
Переменные s1,s3,s4,r1 – базисные, так как входят в одно уравнение системы с коэффициентом 1, а в другие с коэффициентом 0. Переменные, которые не являются базисными, называются свободными переменными.
Для получения единичного базиса нам пришлось ввести искусственные переменные, поэтому начальное решение является псевдорешением. Для нахождения начального опорного решения функции L, сначала придется решить вспомогательную задачу.
Вспомогательная задача описывается функцией: W=-r1. Если W=0, то это означает, что все искусственные переменные обращаются в нуль. В таком случае будет найдено начальное опорное решение функции L. В противном случае, решений не существует.
Замечание 1: При составлении симплекс таблицы, коэффициенты при переменных функции L записываются с противоположными знаками, а свободный член со своим знаком.
Замечание 2: Функции L и W не содержат базисных переменных.
Каноническая форма задачи:
Составляем начальную симплекс – таблицу и решаем первую задачу ЛП на максимум.
баз |
x1 |
x2 |
x3 |
s1 |
s2 |
s3 |
r1 |
Реш-е |
отн |
x3 |
5 |
-2 |
1 |
0 |
0 |
0 |
0 |
3 |
0,60 |
r1 |
1 |
1 |
0 |
-1 |
0 |
0 |
1 |
1 |
1,00 |
s2 |
-3 |
1 |
0 |
0 |
1 |
0 |
0 |
3 |
- |
s3 |
2 |
1 |
0 |
0 |
0 |
1 |
0 |
4 |
2,00 |
L |
-7 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
- |
W |
-1 |
-1 |
0 |
1 |
0 |
0 |
0 |
-1 |
- |
баз |
x1 |
x2 |
x3 |
s1 |
s2 |
s3 |
r1 |
Реш-е |
отн |
x3 |
1 |
-0,4 |
0,2 |
0 |
0 |
0 |
0 |
0,6 |
0,60 |
r1 |
1 |
1 |
0 |
-1 |
0 |
0 |
1 |
1 |
1,00 |
s2 |
-3 |
1 |
0 |
0 |
1 |
0 |
0 |
3 |
- |
s3 |
2 |
1 |
0 |
0 |
0 |
1 |
0 |
4 |
2,00 |
L |
-7 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
- |
W |
-1 |
-1 |
0 |
1 |
0 |
0 |
0 |
-1 |
- |
баз |
x1 |
x2 |
x3 |
s1 |
s2 |
s3 |
r1 |
Реш-е |
отн |
х1 |
1 |
-0,4 |
0,2 |
0 |
0 |
0 |
0 |
0,6 |
- |
r1 |
0 |
1,4 |
0,2 |
-1 |
0 |
0 |
1 |
0,4 |
0,29 |
s2 |
0 |
-0,2 |
0,6 |
0 |
1 |
0 |
0 |
4,8 |
- |
s3 |
0 |
-1,8 |
-0,4 |
0 |
0 |
1 |
0 |
2,8 |
1,56 |
L |
0 |
-0,8 |
1,4 |
0 |
0 |
0 |
0 |
4,2 |
- |
W |
0 |
-1,4 |
0,2 |
1 |
0 |
0 |
0 |
-0,4 |
- |
баз |
x1 |
x2 |
x3 |
s1 |
s2 |
s3 |
r1 |
Реш-е |
х1 |
1 |
-0,4 |
0,2 |
0 |
0 |
0 |
0 |
0,6 |
r1 |
0 |
1 |
-0,14 |
-0,71 |
0 |
0 |
0,71 |
0,29 |
s2 |
0 |
-0,2 |
0,6 |
0 |
1 |
0 |
0 |
4,8 |
s3 |
0 |
-1,8 |
-0,4 |
0 |
0 |
1 |
0 |
2,8 |
L |
0 |
-0,8 |
1,4 |
0 |
0 |
0 |
0 |
4,2 |
W |
0 |
-1,4 |
0,2 |
1 |
0 |
0 |
0 |
-0,4 |
баз |
x1 |
x2 |
x3 |
s1 |
s2 |
s3 |
Реш-е |
отн |
х1 |
1 |
0 |
0,14 |
-0,29 |
0 |
0 |
0,71 |
- |
x2 |
0 |
1 |
-0,14 |
-0,71 |
0 |
0 |
0,29 |
- |
s2 |
0 |
0 |
0,57 |
-0,14 |
1 |
0 |
4,86 |
- |
s3 |
0 |
0 |
-0,14 |
1,29 |
0 |
1 |
2,29 |
1,78 |
L |
0 |
0 |
1,29 |
-0,57 |
0 |
0 |
4,43 |
- |
баз |
x1 |
x2 |
x3 |
s1 |
s2 |
s3 |
Реш-е |
х1 |
1 |
0 |
0,14 |
-0,29 |
0 |
0 |
0,71 |
Х2 |
0 |
1 |
-0,14 |
-0,71 |
0 |
0 |
0,29 |
s2 |
0 |
0 |
0,57 |
-0,14 |
1 |
0 |
4,86 |
s3 |
0 |
0 |
-0,11 |
1 |
0 |
0,8 |
1,78 |
L |
0 |
0 |
1,29 |
-0,57 |
0 |
0 |
4,43 |
баз |
x1 |
x2 |
x3 |
s1 |
s2 |
s3 |
Реш-е |
х1 |
1 |
0 |
0,11 |
0 |
0 |
0,2 |
1,22 |
x2 |
0 |
1 |
-0,22 |
0 |
0 |
0,6 |
1,56 |
s2 |
0 |
0 |
0,56 |
0 |
1 |
0,1 |
5,11 |
s1 |
0 |
0 |
-0,11 |
1 |
0 |
0,8 |
1,78 |
L |
0 |
0 |
1,22 |
0 |
0 |
0,4 |
5,44 |
Ответ: x1=1,22; x2=1,56; L=5,44. Результат совпадает с графическим методом.
Теперь решим задачу на минимум.
баз |
x1 |
x2 |
x3 |
s1 |
s2 |
s3 |
r1 |
Реш-е |
отн |
x3 |
5 |
-2 |
1 |
0 |
0 |
0 |
0 |
3 |
0,60 |
r1 |
1 |
1 |
0 |
-1 |
0 |
0 |
1 |
1 |
1,00 |
s2 |
-3 |
1 |
0 |
0 |
1 |
0 |
0 |
3 |
- |
s3 |
2 |
1 |
0 |
0 |
0 |
1 |
0 |
4 |
2,00 |
L |
-7 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
- |
W |
-1 |
-1 |
0 |
1 |
0 |
0 |
0 |
-1 |
- |
баз |
x1 |
x2 |
x3 |
s1 |
s2 |
s3 |
r1 |
Реш-е |
отн |
x3 |
1 |
-0,4 |
0,2 |
0 |
0 |
0 |
0 |
0,6 |
0,60 |
r1 |
1 |
1 |
0 |
-1 |
0 |
0 |
1 |
1 |
1,00 |
s2 |
-3 |
1 |
0 |
0 |
1 |
0 |
0 |
3 |
- |
s3 |
2 |
1 |
0 |
0 |
0 |
1 |
0 |
4 |
2,00 |
L |
-7 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
- |
W |
-1 |
-1 |
0 |
1 |
0 |
0 |
0 |
-1 |
- |
баз |
x1 |
x2 |
x3 |
s1 |
s2 |
s3 |
r1 |
Реш-е |
x1 |
1 |
-0,4 |
0,2 |
0 |
0 |
0 |
0 |
0,6 |
r1 |
0 |
1,4 |
-0,2 |
-1 |
0 |
0 |
1 |
0,4 |
s2 |
0 |
-0,2 |
0,6 |
0 |
1 |
0 |
0 |
4,8 |
s3 |
0 |
1,8 |
-0,4 |
0 |
0 |
1 |
0 |
2,8 |
L |
0 |
0,8 |
-1,4 |
0 |
0 |
0 |
0 |
-4,2 |
W |
0 |
-1,4 |
0,2 |
1 |
0 |
0 |
0 |
-0,4 |
баз |
x1 |
x2 |
x3 |
s1 |
s2 |
s3 |
r1 |
Реш-е |
x1 |
1 |
-0,4 |
0,2 |
0 |
0 |
0 |
0 |
0,6 |
r1 |
0 |
1,4 |
-0,2 |
-1 |
0 |
0 |
1 |
0,4 |
s2 |
0 |
-0,2 |
0,6 |
0 |
1 |
0 |
0 |
4,8 |
s3 |
0 |
1,8 |
-0,4 |
0 |
0 |
1 |
0 |
2,8 |
L |
0 |
0,8 |
-1,4 |
0 |
0 |
0 |
0 |
-4,2 |
W |
0 |
-1,4 |
0,2 |
1 |
0 |
0 |
0 |
-0,4 |
баз |
x1 |
x2 |
x3 |
s1 |
s2 |
s3 |
r1 |
Реш-е |
отн |
|
x1 |
1 |
-0,4 |
0,2 |
0 |
0 |
0 |
0 |
0,6 |
- |
|
r1 |
0 |
1 |
-0,14 |
-0,71 |
0 |
0 |
1,71 |
0,28 |
0,28 |
|
s2 |
0 |
-0,2 |
0,6 |
0 |
1 |
0 |
0 |
4,8 |
- |
|
s3 |
0 |
1,8 |
-0,4 |
0 |
0 |
1 |
0 |
2,8 |
1,56 |
|
L |
0 |
0,8 |
-1,4 |
0 |
0 |
0 |
0 |
-4,2 |
- |
|
W |
0 |
-1,4 |
0,2 |
1 |
0 |
0 |
0 |
-0,4 |
- |
|
баз |
x1 |
x2 |
x3 |
s1 |
s2 |
s3 |
Реш-е |
|
||
x1 |
1 |
0 |
0,14 |
0,29 |
0 |
0 |
0,71 |
|
||
r1 |
0 |
1 |
-0,14 |
-0,71 |
0 |
0 |
0,28 |
|
||
s2 |
0 |
0 |
0,57 |
-0,14 |
1 |
0 |
0,14 |
|
||
s3 |
0 |
0 |
-0,14 |
1,29 |
0 |
1 |
-1,28 |
|
||
L |
0 |
0 |
-1,28 |
0,57 |
0 |
0 |
-0,57 |
|
||
W |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
||
баз |
x1 |
x2 |
x3 |
s1 |
s2 |
s3 |
Реш-е |
отн |
x1 |
1 |
0 |
0,14 |
0,29 |
0 |
0 |
0,71 |
5 |
x2 |
0 |
1 |
-0,14 |
-0,71 |
0 |
0 |
0,28 |
- |
s2 |
0 |
0 |
0,57 |
-0,14 |
1 |
0 |
0,14 |
8,75 |
s3 |
0 |
0 |
-0,14 |
1,29 |
0 |
1 |
-1,28 |
- |
L |
0 |
0 |
-1,28 |
0,57 |
0 |
0 |
-0,57 |
- |
баз |
x1 |
x2 |
x3 |
s1 |
s2 |
s3 |
Реш-е |
отн |
x1 |
1 |
0 |
1 |
-2 |
0 |
0 |
5 |
5 |
x2 |
0 |
1 |
-0,14 |
-0,71 |
0 |
0 |
0,28 |
- |
s2 |
0 |
0 |
0,57 |
-0,14 |
1 |
0 |
0,14 |
8,75 |
s3 |
0 |
0 |
-0,14 |
1,29 |
0 |
1 |
-1,28 |
- |
L |
0 |
0 |
-1,28 |
0,57 |
0 |
0 |
-0,57 |
- |
баз |
x1 |
x2 |
x3 |
s1 |
s2 |
s3 |
Реш-е |
x3 |
7 |
0 |
1 |
-2 |
0 |
0 |
5 |
x2 |
1 |
1 |
0 |
-1 |
0 |
0 |
1 |
s2 |
-4 |
0 |
0 |
1 |
1 |
0 |
2 |
s3 |
1 |
0 |
0 |
1 |
0 |
1 |
3 |
L |
9 |
0 |
0 |
-2 |
0 |
0 |
2 |
баз |
x1 |
x2 |
x3 |
s1 |
s2 |
s3 |
Реш-е |
x3 |
7 |
0 |
1 |
-2 |
0 |
0 |
5 |
x2 |
1 |
1 |
0 |
-1 |
0 |
0 |
1 |
s2 |
-4 |
0 |
0 |
1 |
1 |
0 |
2 |
s3 |
1 |
0 |
0 |
1 |
0 |
1 |
3 |
L |
9 |
0 |
0 |
-2 |
0 |
0 |
2 |
баз |
x1 |
x2 |
x3 |
s1 |
s2 |
s3 |
Реш-е |
x3 |
-1 |
0 |
1 |
0 |
2 |
0 |
9 |
x2 |
-3 |
1 |
0 |
0 |
1 |
0 |
3 |
s1 |
-4 |
0 |
0 |
1 |
1 |
0 |
2 |
s3 |
5 |
0 |
0 |
0 |
-1 |
1 |
1 |
L |
1 |
0 |
0 |
0 |
2 |
0 |
6 |
Ответ: x1=0; x2=3; L=6. Результат совпадает с графическим методом.