1.3Нейрон

Н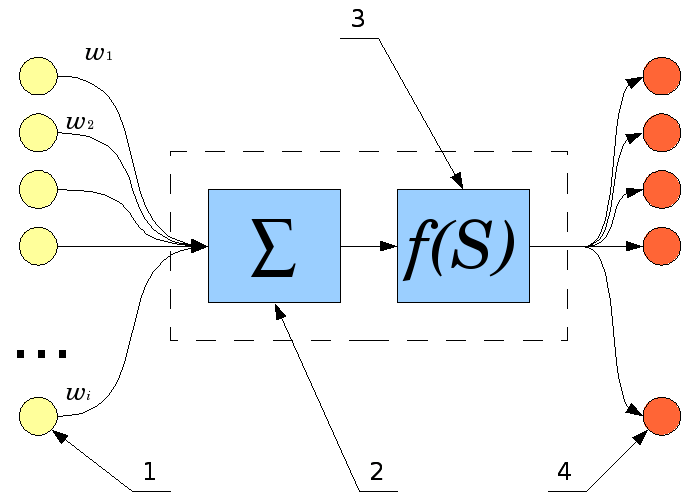 ейрон являє собою одиницю обробки інформації в нейронної мережі. На малюнку нижче наведена модель нейрона, що лежить в основі штучних нейронних мереж.

Синапси, кожен з яких характеризується своєю вагою або силою. Здійснюють зв'язок між нейронами, множать вхідний сигнал на ваговий коефіцієнт синапсу, що характеризує силу синаптичної зв'язку;

суматор, аналог тіла клітини нейрона. Виконує додавання зовнішніх вхідних сигналів або сигналів, що надходять по синаптическим зв'язках від інших нейронів. Визначає рівень збудження нейрона;

функція активації, визначає остаточний вихідний рівень нейрона, з яким сигнал збудження (гальмування) надходить на синапси наступних нейронів.

Модель нейрон імітує в першому наближенні властивості біологічного нейрона. На вхід штучного нейрона надходить деяка безліч сигналів, кожен з яких є виходом іншого нейрона. Кожен вхід множиться на відповідну вагу, пропорційний синаптичної силі, і всі твори сумуються, визначаючи рівень активації нейрона.

Хоча мережеві парадигми досить різноманітні, в основі майже всіх їх лежить ця модель нейрона. Тут безліч вхідних сигналів, позначених   надходить на штучний нейрон. Ці вхідні сигнали, в сукупності позначаються вектором , відповідають сигналам, що приходять в синапси біологічного нейрона. Кожен сигнал множиться на відповідну вагу і надходить на суммирующий блок, позначений ,. Кожна вага   відповідає «силі» однієї біологічної синаптичної зв'язку. Безліч ваг в сукупності позначається вектором . Суммирующий блок, що відповідає тілу біологічного елемента, складає зважені входи алгебраїчно створюючи вихід . Далі надходить на вхід функції активації, визначаючи остаточний сигнал збудження або гальмування нейрона на виході. Цей сигнал надходить на синапси наступних нейронів і т.д.

Розглянута проста модель нейрона ігнорує багато властивості свого біологічного двійника. Наприклад, вона не бере до уваги затримки в часі, які впливають на динаміку системи. Вхідні сигнали відразу ж породжують вихідний сигнал. І, що більш важливо, дана модель нейрона не враховує впливів функції частотної модуляції або синхронизирующей функції біологічного нейрона, які ряд дослідників вважають вирішальними. Незважаючи на ці обмеження, мережі, побудовані на основі цієї моделі нейрона, виявляють властивості, що сильно нагадують біологічну систему. Тільки час і дослідження зможуть відповісти на питання, чи є подібні збіги випадковими або наслідком того, що саме в цій моделі нейрона вірно схоплені найважливіші риси біологічного прототипу.

1.4Функції активації в нейронних мережах

Функція активації (активаційна функція, функція збудження) - функція, що обчислює вихідний сигнал штучного нейрона. Як аргумент приймає сигнал   , одержуваний на виході вхідного суматора   . Найбільш часто використовуються наступні функції активації.

1. Одиничний стрибок або жорстка порогова функція

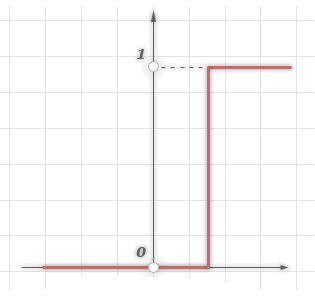Проста кусково-лінійна функція. Якщо вхідна значення менше порогового, то значення функції активації одно мінімального допустимого, інакше - максимально допустимому.

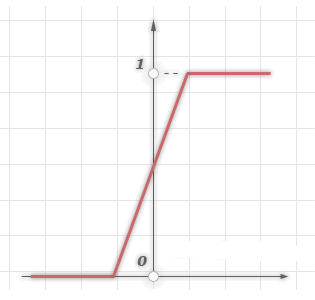. 2.Лінійний поріг або гістерезис

Нескладна кусково-лінійна функція. Має два лінійних ділянки, де функція активації тотожно дорівнює мінімально допустимому і максимально допустимому значенню і є ділянка, на якому функція строго монотонно зростає.

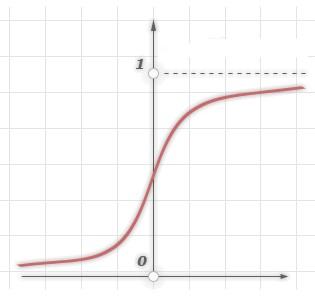3.Сигмоїдальна функція або сигмоид

Монотонно зростаюча всюди дифференцируемая-подібна нелінійна функція з насиченням. Сигмоид дозволяє підсилювати слабкі сигнали і не насичуватися від сильних сигналів. Гросберг (1973 рік) виявив, що подібна нелінійна функція активації вирішує поставлену їм дилему шумового насичення.

Прикладом сигмоїдальної функції активації може служити логістична функція, що задається наступним виразом:

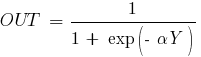
де     - параметр нахилу сигмоїдальної функції активації. Змінюючи цей параметр, можна побудувати функції з різною крутизною.