III. Нелинейные инварианты линейных циклов и собственные полиномы линейных операторов

В общем случае невырожденный линейный оператор в подходящем базисе может быть представлен матрицей - жордановой формой [12, 13].

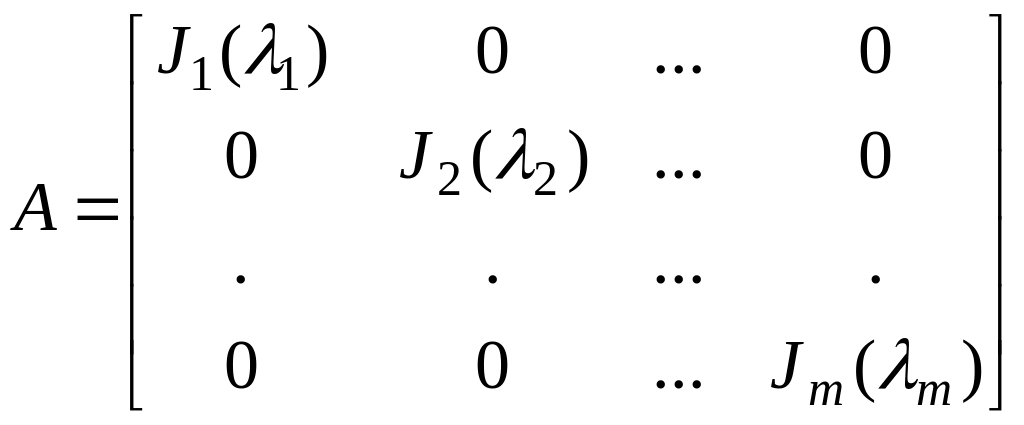, (4)

где - жордановы клетки разных размеров. Жорданова клетка имеет вид

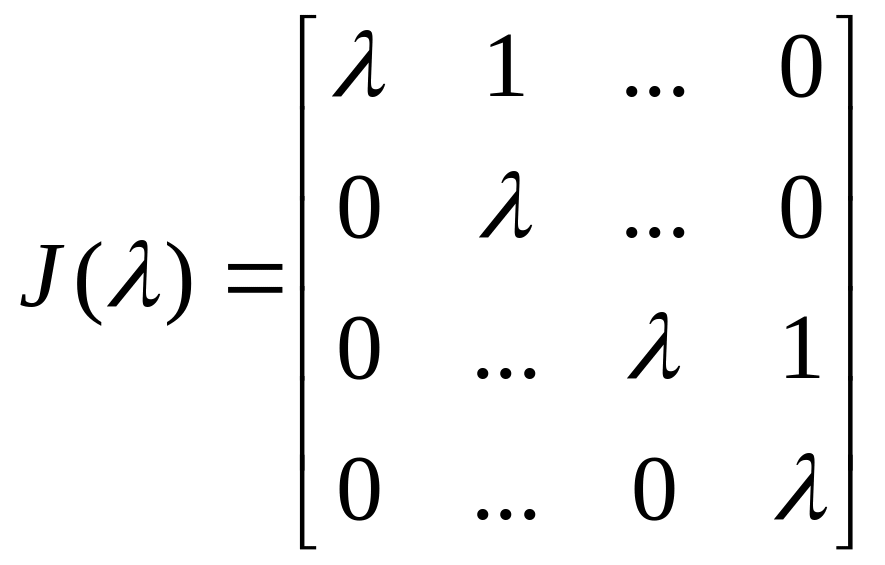(5)

Таким образом, теорема 2 относится только к тем строкам матрицы линейного оператора , которые соответствуют собственным векторам , т.е. к совокупности последних строк жордановых клеток , . Ниже мы распространим эту теорему на произвольные невырожденные линейные операторы, введя в рассмотрение жордановы клетки в целом.

2. Собственные полиномы жордановых клеток

Для анализа линейных циклов линейный оператор следует рассматривать как линейное преобразование переменных линейного пространства однородных полиномов некоторой степени . Преобразование определяет линейное преобразование пространства в себя (гомоморфизм) . Для оно задано формулой

.

Определение 3. Полином называется собственным полиномом линейного оператора с собственным числом , если - собственный вектор , т.е. . Таким образом, собственный полином определяется формулой

. (6)

Замечание 2. Понятия собственного многочлена и L-инварианта линейного оператора – некоторые аналоги понятий основных понятий геометрической теории инвариантов – а именно, понятий относительного и абсолютного инвариантов группы преобразований векторного пространства в том случае, когда эта группа определена как циклическая c образующим элементом : [15].

Пример 1. Пусть - собственный вектор оператора и - его собственное значение. Тогда - собственный полином оператора с собственным числом .

Предположим, что линейный оператор состоит из одной жордановой клетки вида (5), которую обозначим через . Если размеры клетки и ее собственное значение в данном контексте не играют роли, их обозначения мы будем игнорировать, обозначая оператор через . Приведем решение задачи построения всех собственных полиномов жордановой клетки .

Теорема. Не существует собственных полиномов от двух переменных .

Доказательство. для любого .

Рассмотрим однородные многочлены степени от переменных . Пусть - последовательность подпространств, определенная в (8).

Теорема 3. Существует система многочленов , , ,…, степени и многочлен степени такие, что многочлен

(9)

является собственным многочленом оператора .

Пример 2. Последовательность собственных полиномов жордановой клетки в пространстве .

, .

, .

, .

, .

Теорема 4. Для жордановой клетки существует набор , состоящий из собственного полинома вида (9): ,

…, .

Любой собственный полином жордановой клетки можно представить в виде

. (15)

где - многочлен от переменной с коэффициентами из .

Замечание 2. Отметим, что формулы (16) по существу определяют изоморфное отображение векторного пространства однородных полиномов степени в векторное пространство собственных полиномов , элементы которого имеют вид , где - взвешенно-однородный полином с весами переменных

.

Система образующих пространства состоит из собственных полиномов и переменной :

.

В системе образующих матрица оператора имеет вид

.

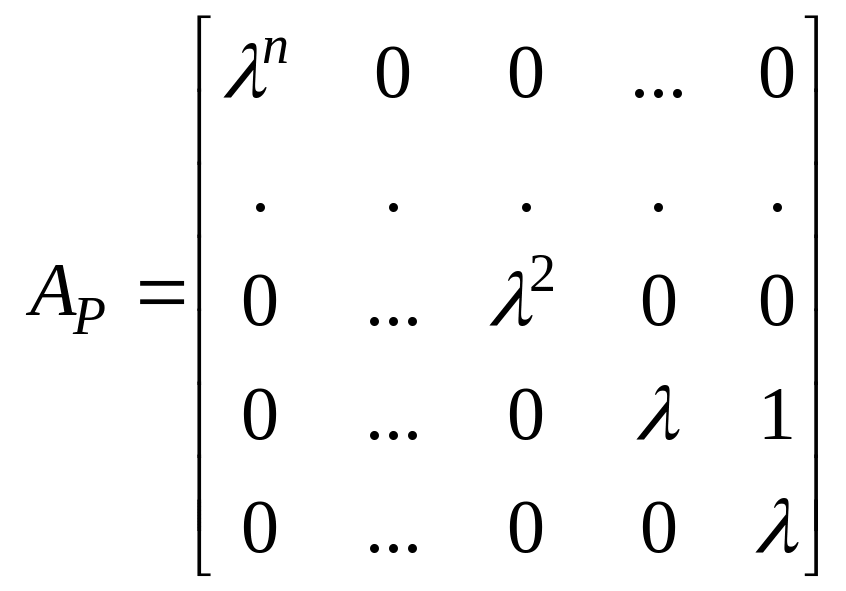Пример 3.

Для системы образующих примера 2 формулы обратных преобразований имеют вид:

В качестве примера этих преобразований рассмотрим задачу выражения собственного полинома 2-ой степени от переменных через систему образующих . Пусть

Вычислим преобразования каждого из мономов . Получим:

.

.

.

.

.

.

Просуммируем полученные равенства и выделим полином, не зависящий от :

Это и есть представление в системе собственных образующих . Осталось проверить, что все коэффициенты при мономах, зависящих от , равны .