II. Полиномиальные инварианты линейных циклов

Введение

Задача генерации полиномиальных инвриантов для произвольных полиномиально определенных программ, повидимому, является очень сложной. Ключевое место здесь – анализ циклов вида

X := b;

While Q(X, b) do X := F(X)

где - условие, - полиномиальное отображение . Пусть . Имеет смысл рассмотреть частные случаи

1. . Циклы с одной переменной в теле цикла

2. Циклы с линейным оператором в теле цикла.

L-инварианты линейных отображений и инварианты линейных циклов

Определение 1. Пусть - n-мерное векторное пространство над полем рациональных чисел и - алгебраическое замыкание поля . Обозначим через - мерный вектор переменных. Рациональная функция называется L-инвариантом линейного оператора , если для любого вектора имеет место соотношение

(1)

Пример 0.

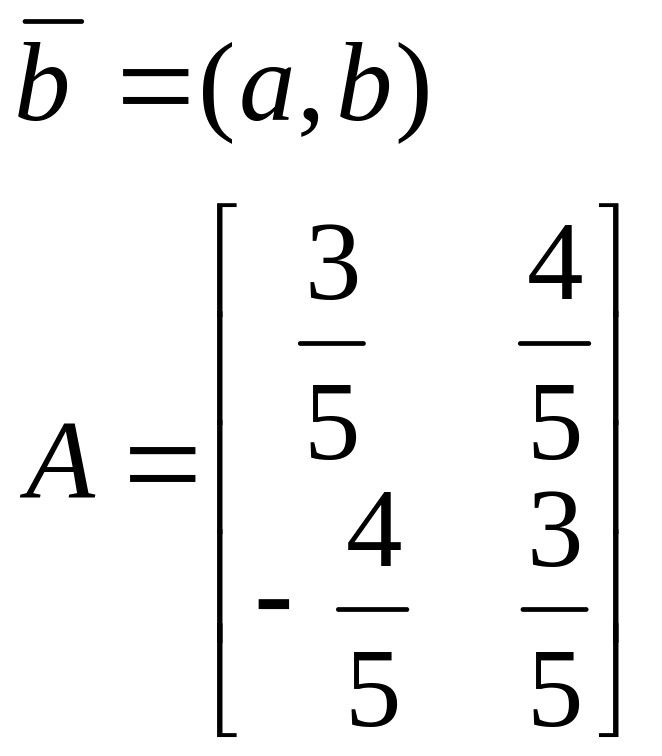
Пример 1. (линейный оператор с характеристическим многочленом )

Рассмотрим линейный оператор с матрицей

, .

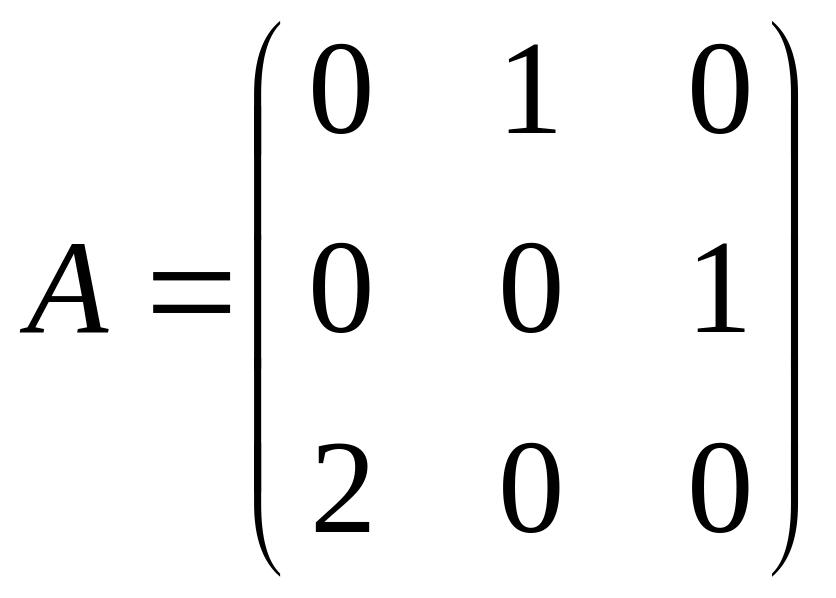Покажем, что рациональное выражение

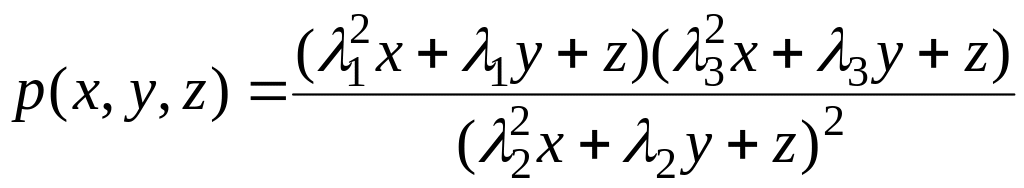(2)

где а - первообразный корень степени 3 из 1 – L–инвариант этого оператора.

=

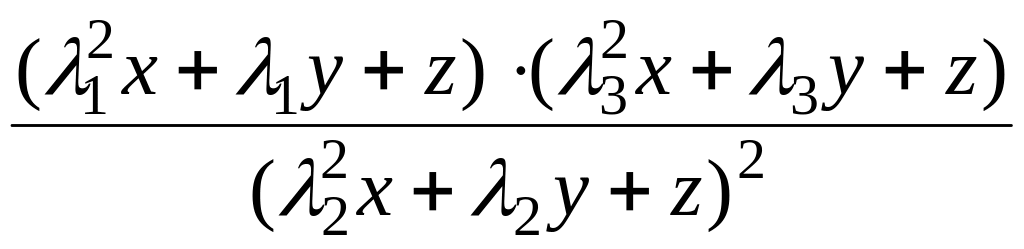
Определение 2. Пусть , - два набора переменных. Линейным циклом мы называем фрагмент императивной программы вида

X := b;

While Q(X, b) do X := A*X

Замечание. Операторы X:=b, X:=A*X интерпретируются как одновременные присвоения переменным левых частей значений правых частей. В дальнейшем условие Q(X, b) мы будем игнорировать, считая линейный цикл бесконечным, а его выполнение недетерминированным. Т.о. мы рассматриваем циклы вида

X := b;

While True|False do X := A*X

Предложение 1. Если - L-инвариант линейного оператора , многочлен - инвариант линейного цикла над полем . Такие инварианты циклов мы будем также называть L-инвариантами (линейных циклов).

Пример 2. (линейный цикл с оператором примера 1)

Линейный цикл, соответствующий оператору , имеет вид

(x, y, z) := (a, b, c);

While True|False do (x, y, z) := (y, z, 2*x)

L-инвариант этого цикла определен формулой (2):

(3)

Отметим, что L-инвариант цикла определен над полем . Однако ему соответствует набор L-инвариантов с коэффициентами из поля , которые можно построить, приведя (3) к каноническому виду – многочлену от , а затем – к многочлену от , используя соотношение и соотношения Виета. Продемонстрируем технику вычисления L-инвариантов над полем .

Введем обозначения

,

Многочлены определены над полем . Вычислим в виде многочленов от . Получим:

, ,

где

, ,

, , (4)

Дробь представима в виде многочлена от с коэффициентами из .

,

(5)

можно вычислить методом неопределенных коэффициентов, используя равенство (5). Осталось заметить, что - L-инварианты оператора . В самом деле,

Поскольку , имеем

Ввиду линейной независимости векторов над

, , ,

т.е , , - L-инварианты над .

Отметим, что если переменным придать числовые значения, L-инвариант преобразуется в инвариант цикла.

Метод построения L-инвариантов, который мы будем рассматривать, заключается в вычислении и анализе собственных значений и собственных векторов линейных операторов.

Предложение 2. Пусть - собственные значения линейного оператора и - соответствующие им собственные векторы сопряженного оператора Предположим, что существуют такие целые числа , что

. (6)

Тогда

(7)

- L-инвариант линейного оператора .

Доказательство. Пусть . Тогда

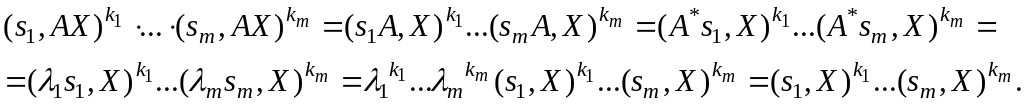
Соотношение (6) мы будем называть мультипликативным соотношением (между корнями характеристического многочлена), определяющим L-инвариант (7).

Пример 3 (продолжение примера 2). Рассмотрим метод предложения 2 применительно к примеру 2. Вычислим собственные числа оператора

, . Т.о. характеристический многочлен имеет вид . Его корни - , ( - первообразный корень степени 3 из 1).

Вычислим далее собственные векторы матрицы 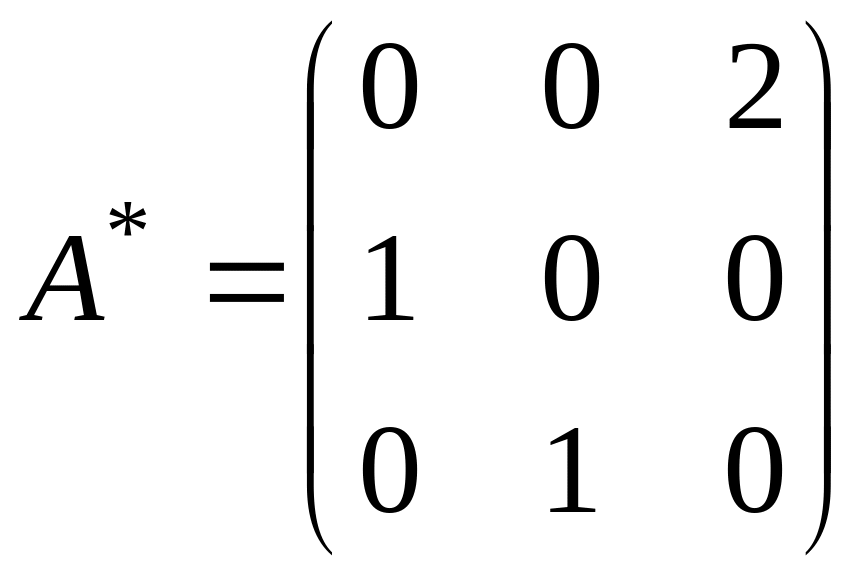. Решим для этого систему однородных линейных уравнений , причем вычисления будем осуществлять в поле по модулю . Получим систему линейных уравнений

, ранг которой равен 2. Фундаментальное решение этой системы – вектор . Поэтому собственными векторами оператора являются векторы

.

Легко установить, что . Поэтому оператор имеет L-инвариант (2).

Следствие 1. Если характеристический (минимальный) многочлен линейного оператора имеет свободный член, равный (т.е. ), линейный оператор обладает L-инвариантом .

Доказательство. Пусть – свободный член многочлена . Тогда . Поэтому либо , либо ( - L-инвариант оператора . Отметим, что коэффициенты этого полинома принадлежат , поскольку они симметричны относительно перестановок корней .

Пример 4. Цикл поворота точки плоскости на угол .

(x,y) := (a,b);

While True do (x, y):= (4/5*x - 3/5*y, 3/5*x + 4/5*y)

Вычислим собственные значения и собственные векторы оператора :

. .

. .

Поскольку , L-инвариант оператора имеет вид

.

Инвариант цикла имеет вид .

Пример 5. Цикл вычисления последовательности Фибоначчи, начиная с пары .

(x,y) := (a,b);

While True|False do (x, y):= (x + y, x)

Вычислим собственные значения и собственные векторы оператора :

. .

. .

Поскольку , L-инвариант оператора имеет вид

.

Инвариантное соотношение цикла имеет вид .

Следствие 2. Если характеристический (минимальный) многочлен линейного оператора имеет вид , линейный оператор обладает L-инвариантами.

Доказательство. Корни характеристического многочлена определены формулой , где - первообразный корень степени из 1. Легко видеть, что если - целые числа такие, что , то - некоторая степень . В самом деле,

,

где . Поэтому произведение в подходящей степени равно 1.

Итак, L-инварианты оператора существуют и вычисляется аналогично тому, как это сделано в примере 3. В частности, L-инвариантами оператора являются рациональные выражения

,

где - собственные векторы , а - наименьшие натуральные числа такие, что кратно : .

Предложение 3. Пусть - многочлен от переменной с рациональными коэффициентами и - все его корни из алгебраического замыкания поля . Рассмотрим множество - множество мономов из поля рациональных выражений (возможно, с отрицательными степенями), которые при подстановке вместо получают значение 1. Тогда - мультипликативная абелева группа с конечным числом образующих.

Доказательство. Каждому моному поставим в соответствие бином кольца следующим образом: моном представим в виде дроби , в числителе которой запишем степени переменных с положительными показателями, а в знаменателе – степени переменных с отрицательными показателями, взятыми со знаком «минус»: .

Группа , очевидно, может быть определена и множеством выше определенных биномов: . Во множестве биномов можно выделить конечное подмножество , которое образует базис идеала кольца , порожденного множеством : . Построим базис Гребнера этого идеала, опираясь на базис . Легко видеть, что S-полином пары биномов также является биномом. Кроме того, редукция бинома заключается в замене на . Поэтому процесс построения базиса Гребнера приводит к конечному множеству биномов, которое мы будем обозначать через Каждый элемент , в свою очередь, определяет моном рассматриваемого нами вида. Обозначим множество таких мономов через . Осталось показать, что образует множество, порождающее группу .

Пусть , . Обозначим через биномы из – элементы базиса Гребнера. (Обозначения переменных в формулах мы опускаем.) Поскольку - базис Гребнера, бином редуцируется к нулю с помощью элементов «исчерпыванием». Это означает, что на каждом шаге редуцирования существует такой номер базисного элемента, что . Шаг редуцирования исчерпыванием состоит в следующем преобразовании: . Этому преобразованию поставим в соответствие следующее преобразование монома - элемента :

Таким образом, шаг редуцирования применительно к элементам состоит в выделении в мономе сомножителя . Редуцированный бином, если это необходимо, следует переупорядочить так, чтобы первый его моном был больше второго. Это преобразование состоит в следующем: . Понятно, что после этого преобразования в мономе выделяются сомножители знаменателя: . Итак, мы показали, что процесс редуцирования исчерпыванием соответствует процессу разложения монома в произведение базисных мономов (возможно, с отрицательными показателями). Теорема доказана.

Пример 6 (Продолжение примера 3). Легко видеть, что для многочлена имеют место следующие мультипликативные соотношения между его корнями:

Этим соотношениям соответствуют биномы

,

которые образуют базис Гребнера идеала .

Следствие 1. Пусть - многочлен от переменной с рациональными коэффициентами и - все его корни из алгебраического замыкания поля . Рассмотрим множество - множество мономов из поля рациональных выражений (возможно, с отрицательными степенями), которые при подстановке вместо получают рациональные значения. Тогда - мультипликативная абелева группа с конечным числом образующих.

Доказательство по существу повторяет доказательство предложения 3. Вместо биномов вида следует рассматривать биномы вида . Более того, вместо поля можно рассматривать любую мультипликативную подгруппу .

Следствие 2. Множество всех L-инвариантов оператора образует поле рациональных выражений.

Доказательство очевидно. Поле L-инвариантов оператора , порожденное элементами , имеет конечное число образующих – элементов .

Проблему описания всех L-инвариантов линейного оператора можно теперь уточнить как проблему построения конечного множества образующих группы .

Определение 3. L-инварианты оператора , определенные мультипликативным соотношением между корнями характеристического многочлена , будем называть целыми. L-инварианты оператора , определенные мультипликативным соотношением , будем называть рациональными.

Предложение 5. Если характеристический многочлена оператора имеет вид , оператор обладает рациональными L-инвариантами.

Доказательство. Пусть - корни многочлена . Тогда . Каждый из сомножителей вида определяет рациональные L-инварианты, которые вычисляются аналогично тому, как это сделано в следствии 2 предложения 2.