Лекция 7. Обработка физического эксперимента

1.Сплайновая интерполяция

2. Интерполяция по общей формуле Лагранжа

3. Реализация полиномиальной регрессии

4. Полиномиальная регрессия

5. Экспоненциальная регрессия

6. Полиномиальная аппроксимация

7. Полиномиальная сплайн-интерполяция

1.Сплайновая интерполяция

Для задания векторов узловых точек VX и VY и заданного аргумента х функция linterp (VX,VY,x) возвращает значение функции при её линейной аппроксимации (интерполяции). При экстраполяции используются отрезки прямых, проведенных через две крайние точки.

При небольшом числе узловых точек (менее 10) линейная интерполяция оказывается довольно грубой. При ней даже первая производная функции аппроксимации испытывает резкие скачки в узловых точках. Для целей экстраполяции функция linterp не предназначена и за пределами области определения может вести себя непредсказуемо.

Гораздо лучшие результаты даёт сплайн-интерполяция. При ней исходная функция заменяется отрезками кубических полиномов, проходящих через три смежные узловые точки. Коэффициенты полиномов, проходящих через три смежные узловые точки. Коэффициенты полиномов рассчитываются так чтобы непрерывными были первая и вторая производные. Линия, которую описывает сплайн-функция, напоминает по форме гибкую линейку, закреплённую в узловых точках.

Для осуществления сплайновой интерполяции система Mathcad предлагает четыре встроенные функции. Три из них служат для получения векторов вторых производных сплайн функций при различных видах интерполяций:

cspline (VX,VY) – возвращает вектор VS вторых производных при приближении в опорных точках к кубическому полиному;

pscline (VX,VY) – возвращает вектор VS вторых производных при приближении в опорных точках к параболической кривой;

lspline (VX,VY) – возвращает вектор VS вторых производных при приближении в опорных точках к прямой.

interp (VS,VX,VY,x) – возвращает значение y(x) для заданных векторов VS,VX,VY и заданного значения х.

Таким образом, сплайн-интерполяция проводится в два этапа. На первом с помощью одной из трех вышеописанных функций отыскивается вектор производных функции y(x), заданной векторами VX и VY её значений (абсцисс ординат). Затем на втором этапе для каждой искомой точки вычисляется y(x) с помощью функции interp.

2. Интерполяция по общей формуле Лагранжа

Эта формула синтезирует полином Лагранжа, за­меняющий зависимость, представленную отдельными точками в виде двух векто­ров VX и VY узловых точек.

Преимущества - частота узловых точек и их рас­положение любое, для интерполяции используется единая интерполяционная формула f(x).

Степень полинома Лагранжа n однозначно связана с числом узловых то­чек. Поэтому график интерполирующей точно проходит через узловые точки, которые могут располагаться как равномерно по оси х, так и неравно­мерно. Формула Лагранжа:

Здесь использована функция if (условие, 1, 2). Если условие выполняется, то вычисляется выражение 1, иначе - 2. ^{В формуле i,j=0…n где n=(число узловых точек-1).}

Если есть 4 узловых точки, то n=3, i=0,i=1,i=2,i=3, VY0,VY1,VY2,VY3.

При j=0, если i=j, то будет 1. При j=1,2,3, если i не равно j, будет считаться по 2 формуле.

3. Реализация полиномиальной регрессии

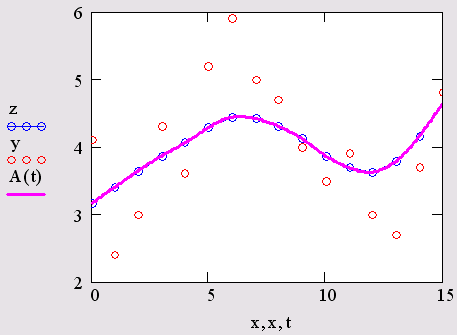
    В Mathcad введена и функция для обеспечения полиномиальной регрессии при произвольной степени полинома регрессии. Регрессия осуществляется функцией regress(VX,VY,n), которая возвращает вектор VS, запрашиваемый функцией interp(VS,VX,VY,x) и содержащий коэффициенты многочлена n-й степени, который наилучшим образом приближает "облако" точек с координатами, хранящимися в векторах VX и VY.     На рис. показан фрагмент документа Mathcad с примером выполнения полиномиальной регрессии. Для вычисления коэффициентов полинома регрессии используется функция submatrix.

создается единственный приближающий полином, коэффициенты которого вычисляются по всей совокупности заданных точек, и который наилучшим образом приближает облако точек к координатам.

Используются функция regress (VX VY, n) - определяет вектор VS, содержащий коэффициенты полинома, который наилучшим образом приближает «облако, точек с координатами в векторах VX, VY. Здесь n - степень полинома, которая должна быть меньше количества заданных точек и обычно n<5;

VS:=regress(VX,VY,n)=|матрица| y(x):=interp(VS, VX, VY, х) - определяет искомую функцию регрессии.

Рис. Полиномиальная регрессия

    На практике не рекомендуется делать степень аппроксимирующего полинома выше 4-6, поскольку погрешности реализации регрессии сильно возрастают.     Функция regress создает единственный приближающий полином, коэффициенты которого вычисляются по всей совокупности заданных точек. Иногда полезна другая функция полиномиальной регрессии, дающая локальные приближения отрезками полиномов второй степени loess(VX,VY,span), которая возвращает вектор VS, используемый функцией interp(VS,VX,VY,x) для наилучшего приближения данных векторов VX и VY отрезками полиномов второй степени. Аргумент span>0 указывает размер локальной области приближаемых данных (рекомендуемое начальное значение - 0,75). Чем больше span, тем сильнее сказывается сглаживание данных. При больших значениях span эта функция приближается к функции regress(VX,VY,2).