5 Исследование переходных процессов в электрических цепях Задание

Для электрической цепи (рис.5.1):

определить практическую длительность переходного процесса ток в цепи и энергию электрического или магнитного поля при t = 2τ. Построить графики i=f(t) и e_L=f(t).

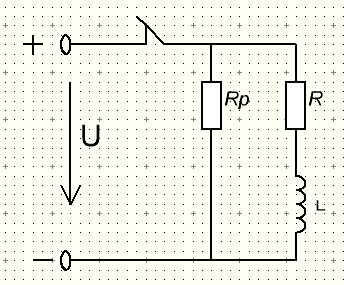
Рисунок 5- Исследуемая электрическая цепь

Дано:

R=140 Ом;

R_р=60 Ом;

L=0.75 Гн ;

U=200 B.

Рисунок 5.1- Исследуемая электрическая цепь

1. Согласно схеме

i_уст=I= = A (20)

Чтобы найти закон изменения переходного тока, запишем уравнение в общем виде

i= i_уст +i_cв= i_уст+А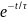

В этой формуле

i_cв= А ,

где i_cв- свободная составляющая тока; А - достоянная интегрирования; е = =2,71 ~ основание натурального логарифма; τ — постоянная времени переходного процесса,

τ=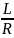 где R- величина сопротивления, через которое про­ходит переходный ток;

t — текущее время.

Определяем постоянную интегрирования, полагая t = 0, тогда уравнение

i= i_уст +i_cв= i_уст+А примет вид:

i₀=i_уст+А т. к. е° = 1

Значит, А = i₀ - i_yст = 0 — I,

то есть А = -I

А=-1.42А (21)

Запишем уравнение (закон изменения переходного тока) при вклю­чении катушки

i=i_ycт+ i_св=i_уст+А = I - I = I×(1 - );

В нашем случае i=1.42×(1 - );

Находим постоянную времени переходного процесса

τ= = τ=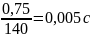 (22)

Практическая длительность переходного процесса

5т = 1.42×0,005= 0,025 с (23)

2. Вычислим значения переходного тока i = f(t), в менты вре­мени t = 0, t = τ , t=2τ, t=3τ, t = 4τ, t = 5 τ.

Значения переходного тока для заданных значений времени:

t=0, i₀=1.42× (1 - 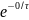) =1.42× (1 -1) = 0 A;

t=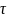 , i₁=1.42× (1 - 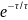) =1.42× (1- 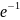) =1.42× (1- 0,367) =0,89 A;

t=2 , i₂=1.42× (1 - ) =1.42× (1 -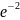 ) = 1.42× (1- 0,135)= 1.22 A

t=3 , i₃=1.42× (1 - ) =1.42× (1 - ) =1.42× (1- 0,049)= 1.35 A; (24)

t=4 , i₄=1.42× (1 - ) =1.42× (1 -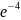 ) = 1.42× (1- 0,018)=1.39 A;

t=5 , i₅=1.42× (1 - ) =1.42× (1 -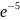 ) =1.42×(1- 0,007)=1.41 A;

Строим график i = f(t).

Закон изменения ЭДС самоиндукции можно получить из формулы

e_L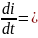=-L -L (I - I ) =-I•L•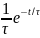 =-I•L• 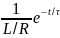=-I•R• =-U

В нашем случае e_L= -200

Значения ЭДС самоиндукции для заданных значений времени следующие:

t=0, e₀₌-200×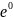 =-200В;

t= , е₁=-200×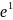 =-200×0,367=-73,4 В;

t=2 , i₂=-200×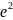 =-200×0,135=-27В;

t=3 , i₃-200×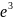 =-200×0,049=-9,8В; (25)

t=4 , i₄=-200×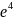 =-=-200×0,018=-3,6 В;

t=5 , i₅=-200×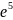 =-200×0,007=-1,4 В;

Строим график e_L = f(t).

3. Энергия магнитного поля при t = 2τ равна:

W_м=L×i₂² 2=0,75×1,2² 2=0,55 Дж. (26)

4. Переключаем переключатель из положения 1 в положения 2 (отключаем катушку от источника постоянного напряжения при одновременном ее замыкании на сопротивление).

В этом случае мы отключаем цепь от источника и при переключении в положение 2 в образовавшемся контуре ток придерживается за счет энергии, накопленной в магнитном поле катушки. Энергия магнитного поля непрерывно уменьшается, так как в активном сопротивлении контура идет необратимый процесс превращения электрической энергии в тепловую.

i=i_ycт+ i_св=i_уст+А

В этом случае i_уст=0, т.к. при отключении цепи от источника ток в цепи будет равен нулю.

Тогда i=А , (27)

где t=L/R+R_p= – постоянная времени переходного процесса.

Определим постоянную интегрирования, пологая t=0, тогда уравнение

i=А , примет вид:

i₀=Аe⁰,т.е. i₀=А,

но i₀=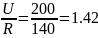 А – согласно первому закону коммутации ток в первый момент коммутации будет таким, каким был в последний момент до коммутации.

Значит, А=1.42А, тогда i= 1.42 A.

Длительность переходного процесса t=5 =5^. 0.004=0.02 c. (28)

Строим график i= f(t), задавшись моментами времени t = 0, t = τ , t=2τ, t=3τ, t = 4τ, t = 5 τ. Данные расчета сведены в таблицу 2.

Таблица 2

t,c	0	τ	2 τ	3 τ	4 τ	5 τ
i,A	1.42	0.52	0.19	0.06	0.02	0.009

5. В соответствии с законом изменения ЭДС самоиндукции получим

e_l=-L =Ue^-t/

В нашем случае

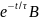e_l=U 200 (29)

Строим график e_l= f(t), задавшись моментами времени t = 0, t = τ , t=2τ, t=3τ, t = 4τ, t = 5 τ. Данные расчета сведены в таблицу 3.

Таблица 3

t,c	0	τ	2 τ	3 τ	4 τ	5 τ
el,	200	73.4	27	9.8	3.6	1.4