4. Jaký je rozdíl mezi diskrétní a spojitou veličinou? Uveďte praktické příklady použití obou těchto typů veličin.

spojitá veličina – se „automaticky“ eviduje, př. Automatický záznam teploty termografem

náhodná veličina – její zjištění, spočtení či výpočet se provádí namátkou, př. Zjišťování počtu studentů na přednášce

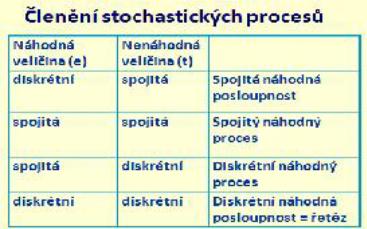
5. Proveďte klasifikaci stochastických procesů podle povahy náhodné a nenáhodné proměnné. Ke každé kategorii uveďte příklad.

6. Jaké problémy jsou řešitelné pomocí Bernouliho posloupnosti? Uveďte praktické příklady a stručně je okomentujte.

problémy, které určují, že se jev A uskuteční právě x-krát

například hod kostkou, mincí

určuju, že jev A nastane či nenastane, to pronásobím mezi sebou a vyjde mi požadovaná pravděpodobnost

Vypočítejte pravděpodobnost, že při 3 hodech kostkou padne alespoň jedna šestka.

p…pravděpodobnost, že padne šestka při jednotlivém hodu

q…pravděpodobnost, že nepadne šestka

Budeme sčítat pravděpodobnosti, že padne 1, 2 nebo 3 šestky.

7. Co je to Poissonův proces? Co vyjadřuje jeho intenzita? Uveďte příklady praktické aplikace a stručně je okomentujte.

Je přirozený nástroj pro modelování řady reálných situací

Je elementární proces v tom smyslu, že při jeho analýze dostáváme obvykle jednoduché výsledky

Je to čítací proces, tj. zkoumá počet výskytů určitého jevu v časovém intervalu. Zkoumaný jev se vyskytuje v náhodných intervalech a jednotlivé výskyty jsou na sobě nezávislé, např. přerušení dodávky elektrické energie, vstup zákazníka do obchodu, zemětřesení, apod

λ...intenzita Poissonova procesu

Př. Skupinová taxi čekají na zákazníky u nádraží. Příchod potencionálních pasažerů je poissonovksý s intenzitou 30 zákazníků za hodinu. Taxi odjíždí jakmile nastoupili 4 zákazníci nebo od nastoupení první uplynolo 10 minut

8. Co je to spojování poissonovských procesů? Jak se provádí?

Spojením několika Poissonových procesů vzniká opět Poissonův proces s intenzitou rovnající se součtu intenzit jednotlivých procesů

STOCHASTICKÉ PROCESY II.

1. Uveďte praktické příklady použití markovských řetězců. Co je markovská vlastnost?

Zjišťování počtu strojů v provozu – modely teorie obnovy, Zjišťování počtu zákazníků, strávníků, Bonus a malus v pojišťovnictví, Vytížení obsluhy, Potřeba lékařů na pohotovosti

2. Co je podmíněná pravděpodobnost přechodu V markovských řetězcích? Co obsahuje vektor absolutních a limitních pravděpodobností markovského řetězce?

2.1. je to stav v okamžiku n+1závisí pouze na stavu v okamžiku n

2.2. vektor absolutních pravděpodobností: je vektor pravděpodobnosí jednotlivých stavů v určitém okamžiku; v okamžiku 0 – vektor počátečních pravděpodobností

Výpočty: vektor absolutních pravděpodobností (řádkový) násobíme maticí přechodu:

p (1) = p(0)*P, p(2) = p(1)*P,…, p(n)= p(n-1)*P

2.3. vektor limitních pravděpodobností: některé řetězce se po určitém počtu krkoku dostanou do stavu, kdy se v dalších okamžicích nemění = konvergují. Jejich stav je potom na čase nezávislý