9. Na jakém principu je založeno cílové programování V modelech vícekriteriální optimalizace? Jak se konstruují cílové omezující podmínky?

Stanovení cíle pro všechny kriteriální funkce

z intervalu daného ideální a bazální hodnotou daného kritéria.

Minimalizace odchylek od zvolených cílů

nedosažení: odchylkové proměnné n;

překročení: odchylkové proměnné p.

Cílové omezující podmínky

levá strana: předpis kriteriální funkce a odchylkové proměnné;

pravá strana: cíl;

typ podmínky: určení (právě rovno).

Nové kritérium: minimalizace odchylek od cílů

oboustranné: z = n + p → min;

jednostranné: penalizujeme pouze horší než cílové hodnoty, ale překročení cílů nám nevadí;

s váhami: váhy použijeme jako cenové koeficienty odchylkových proměnných.

10. Jakým způsobem se zohledňují různé váhy kriteriálních funkcí V modelech cílového programování? Jaký je rozdíl mezi jednostrannou a oboustrannou penalizací odchylek od zadaných cílů?

Metoda pořadí důležitosti, Aspirační úroveň, Bodovací metoda, Polygonální zobrazení variant

STRUKTURNÍ ANALÝZA

1. Uveďte podstatu a význam strukturních modelů.

strukturní model lze charakterizovat jako model, který zobrazuje materiálové, nákladové, pracovní, popřípadě i další vazby mezi složkami daného hospodářského systému navzájem a mezi tímto systémem a jeho okolím pomocí soustavy funkcí

snaží se najít rovnovážný stav systému

Bilance vztahů mezi jednotlivými hospodářskými soubory (odvětvími) – analýza minulého stavu systému

Plánování činnosti systému, využití výrobních zařízení apod.

Možnost sledovat vliv změn v systému při zachování výchozích relací.

Vyčíslení vlivu hodnotových změn - propočty cenových úprav

Určení podmínek hospodářské stability a rovnováhy systému, nikoliv nalezení optimálního stavu.

2. Klasifikujte modely strukturní analýzy podle jejich vazby na okolí a z hlediska časového faktoru. Ke každé kategorii uveďte příklad.

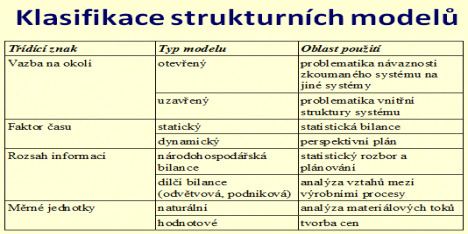
3. Co je to input-output tabulka V modelu strukturní analýzy? Stručně charakterizujte její jednotlivé kvadranty.

První kvadrant – matice meziodvětvových (endogenních) toků

Druhý kvadrant – exogenní (vnější toky) – rozdělení finální produkce (4 sektory – spotřeba obyvatelstva, celospolečenská spotřeba, investiční výstavba a zahraniční obchod)

Třetí kvadrant – spotřeba živé práce, nakoupených materiálů, energie, surovin, apod. (např. odpisy, mzdy, zisky, včetně daní)

Čtvrtý kvadrant – údaje o tocích primárních zdrojů ve finální spotřebě

4. Co vyjadřují technicko-ekonomické koeficienty a normy spotřeby primárních činitelů v modelech strukturní analýzy? Jaká je jejich věcná interpretace?

Ukazují, jaká výše produkce se spotřebovává

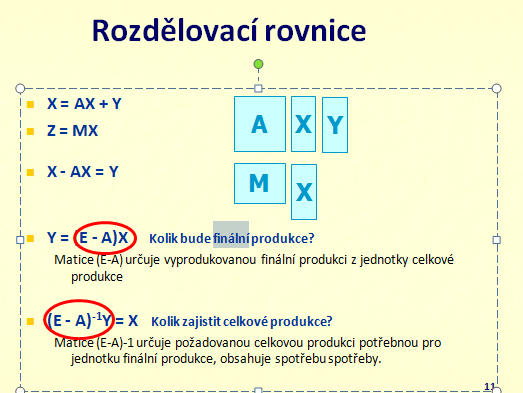
5. Co jsou to rozdělovací rovnice v modelech strukturní analýzy? Pro jaké účely je lze použít?

Vypočítá se z technicko-ekonomických koeficientů a z norem spotřeby primárních činitelů

6. Co je to Leontiefova matice v modelech strukturní analýzy? Jak se určí a co vyjadřují její jednotlivé prvky?

Leontiefova matice (E-A) určuje vyprodukovanou finální produkci z jednotky celkové produkce

Inverzní Leontiefova matice (E-A)-1 určuje požadovanou celkovou produkci potřebnou pro jednotku finální produkce, obsahuje potřebu spotřeby

7. Co je finální a celková produkce v modelu strukturní analýzy a jak se vypočítá?

X = (X₁, X₂, ..., X_n)^T - vektor celkové produkce

Y = (Y₁, Y₂, ..., Y_n)^T - vektor finální produkce

8. Co je smíšená úloha strukturní analýzy?

Jde o úlohu, kdy jen u některých odvětví známe plánovanou celkovou produkci a u zbývajících plánovanou finální produkci.

známe x_k a y_e

9. Jaké hlavní nedostatky vykazují modely strukturní analýzy?

Nelze dobře zobrazit záměnu surovin, technologií nebo kapacit.

Nerespektují při propočtu kapacitní, surovinová a jiná omezení.

Nejsou to modely optimalizační.

Nelze zjistit, je-li rovnovážný stav, o který usilujeme, výhodný

STOCHASTICKÉ PROCESY I.

1. Jaký je rozdíl mezi deterministickým a stochastickým procesem?

Deterministický proces lze odvodit z předchozích jevů

Stochastický proces je závislý pouze na náhodě, nedá se předem určit ani předpovědět

2. Z jakých dvou proměnných se obecně skládá stochastický proces? Tyto proměnné charakterizujte.

X(t) = F(t,e)

e … náhodný jev

t … nenáhodná veličina (obvykle čas)

3. Co je to průsek a realizace stochastického procesu? Jedná se o náhodné funkce? Proč?

3.1. Realizace: realizace náhodného procesu je nenáhodná funkce

e = e₀

F (t, e₀ ) = x (t)

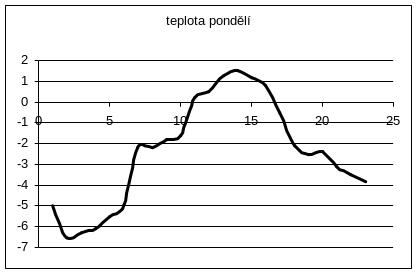
3.2. Průsek: průsek stochastického procesu je náhodná veličina. Má střední hodnotu a rozptyl

t = t₀

F (t₀, e) = X (t)

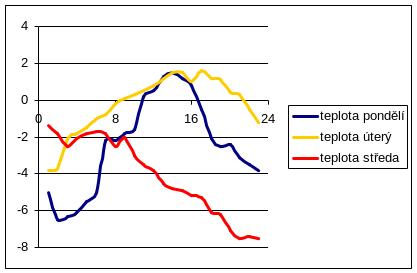
čas	teplota pondělí	teplota úterý	teplota středa	střední hodnota	rozptyl
6	-5	-1	-1,7	-2,6	3