10. Jaká znáte rozhodovací pravidla pro rozhodování za nejistoty vhodná pro optimistického rozhodovatele (alespoň 2)? Stručně popište jejich princip a zdůvodněte, proč jsou optimistická.
10.1. Maximaxové pravidlo: rozhodovatel zvolí alternativu, která přinese nejlepší výplatu, bez ohledu na to, že může nastat i velmi nepříznivý stav okolností a výsledek rozhodnotuí může být podstatně odlišný od výsledku optimisticky očekávaného
10.2. Hurwiczovo pravidlo: je založeno na očekávaní nejlepších a nehorších výsledků každého z nich. Optimista očekává nejlepší výsledky a pesimista zas nejhorší. Skutečný výsledek vybraného rozhodnutí se bude nacháze někdy mezi
11. Jaká znáte rozhodovací pravidla pro rozhodování za nejistoty vhodná pro pesimistického rozhodovatele (alespoň 2)? Stručně popište jejich princip a zdůvodněte, proč jsou pesimistická.
11.1. Waldovo kritérium (maxmin): rozhodovatel nechce riskovat, je konzervativní a přesvědčený o tom, že je „lepší něco než nic“
Především bude analyzovat nevýhodné výplaty, aby si z nich vybral tu nejméně špatnou
Pravidlo se chápe jako „nejlepší z nejhoršího“
11.2. Savageovo kritérium (minimax): vychází ze ztrát, které mohou nastat tím, že volba rizikové varianty nebyla optimální vzhledem k rizikové situaci, která po této volbě nastala. Tyto ztráty pro každou variantu a rizikovou situaci určíme jako rozdíl hodnoty kritéria varianty, která je za této situace optimální, a hodnot dalších variant.
12. Jaká znáte rozhodovací pravidla pro rozhodování za nejistoty vhodná pro rozhodovatele s neutrálním postojem k riziku (alespoň 2)? Stručně popište jejich princip a zdůvodněte jejich neutralitu k riziku.
12.1. Laplaceovo pravidlo: při rozhodování za úplné nejistoty je tzv. princip nedostatečné evidence. Tento přístup se snaží zohlednit všechny výplaty, a proto jednotlivé stavy okolností považuje za stejně pravděpodobné. Rozhodování za podmínek nejistoty je převedeno na rozhodování za podmínek rizika s pptsím vektorem, jehož složky mají hodnotu 1/n
12.2. Hurwiczovo pravidlo - založeno na míře očekávání nejlepších a nejhorších výsledků pro každou strategii. Stanoví se optimisticko pesimistický index
13. Co je to matice ztrát? Co vyjadřuje a jak se určí její prvky?
Prvky z této matice jsou ztráty, ke kterým dojde při špatné volbě strategie inteligentního hráče pro každou strategii přírody
Je to vyčíslení nejhorších hodnot od hodnoty nejlepší, prvky se určí tak, že vezmeme nejlepší možnost a od té odečítáme ty horší a jejich hodnoty zapisujeme do tzv. matice ztrát
TEORIE HRY:
1. Uveďte stručný popis libovolného praktického problému, který by bylo možné řešit pomocí modelu teorie her. Zdůvodněte, proč je použití tohoto modelu v dané situaci adekvátní.
například při sportovním utkání, kdy je záměrem obou stran vyhrát. Každá strana má strategie, které různě kombinuje proti inteligentnímu hráči. Cílem je volba nejlepšího chování v rámci konfliktu. Hra probíhá v čase.
2. Jaké znáte typy modelů teorie her? Uveďte klasifikaci těchto modelů včetně stručného popisu podle alespoň dvou hledisek.
2.1. - hry s inteligentním protihráčem – principem strategické hry je max výhru nebo min prohru, když už nejde vyhrát o antagonistická hra, neantagonistická hra, kooperativní hra, hra s nulovým součtem, ..
2.2. hry proti přírodě – hry za jistoty, za rizika, a úplné nejistoty
3. Uveďte a stručně popište základní komponenty modelu teorie her.
3.1. Komponenty:
Dva hráči
Množiny strategií každého hráče
Výplaty pro každou dvojici strategií
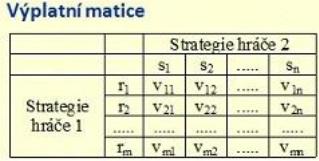
Výplatní matice
Konstantní, resp. nulový součet
4. Co je to model hry v normálním a rozvinutém tvaru? Jaké informace obsahují a jak je reprezentují?
4.1. v rozvinutém tvaru zobrazuje hru pomocí stromu a každou strategii jako posloupnost hran zobrazujících tahy
Pro složitější situace s mnoha možnými různými tahy může být velice rozsáhlý a nepřehledný. (např. popis šachové hry by bylo nutno v každém kroku zobrazit 20 – 30 dalších možných tahů)
4.2. v normální tvaru je zobrazen pomocí tabulky obsahující jednotlivé strategie hráčů a výplaty pro každou kombinaci strategií hráčů.
