Úplný seznam otázek:

TEORIE ROZHODOVÁNÍ

1. Uveďte stručný popis libovolného praktického problému, který by bylo možné řešit pomocí rozhodovacího modelu. Zdůvodněte, proč je použití tohoto modelu V dané situaci adekvátní.

Realitní společnost vlastní pozemky a má se rozhodnout, za kolik, kdy a komu je má prodat (viz skripta strana 123).

2. Co je to rozhodovací proces? Stručně popište jeho jednotlivé fáze.

2.2. Cílem je vybrat tu alternativu, která je z určitého hlediska nejvýhodnější. Efekt, plynoucí z realizace jednotlivých alternativ rozhodnutí, je ovlivňován budoucí situací, která však není rozhodovatelem ovlivnitelná. Explicitně není zřejmé, která z těchto variant je nejlepší, protože v okamžiku rozhodnutí není přesně známo, jaké důsledky pro rozhodovatele její bude mít

2.3. Fáze:

a) Intelligence – zkoumání reality, identifikace a definice problému, systému

b)Design – konstrukce modelu, shromáždění dat, návrhy řešení

c) Choice – výběr řešení modelu

d) Implementation - řešení reálného problému

3. Klasifikujte konfliktní situace. Co rozumíme pojmem „inteligence hráče“?

3.1. Konfliktní situace = situace, ve kterých dochází ke střetu zájmů jednotlivých účastníků konfliktu

3.2. Cílem je najít takové chování každého účastníka, při němž výsledek bude z hlediska každého z nich optimální

3.3. Může mít: Antagonistický (v případě dosažení cíle jedním z účastníků zamězí pozitivnímu výsledku ostatních) nebo neantagonistický (všichni mají možnost více či méně realizovat svoje cíle) charakter

3.4. Klasifikace: důležité je charakteristikovat hráčů podle jejich zájmu a cílů ve hře. Hráči mohou být na výsledky hry zainteresováni a hrát tak, aby vyhráli (= inteligentní hráči) A hráči, kteří se sice účastní, ale výsledek je nezajímá (= neinteligentní hráči). Takový hráči vystupují pouze jako náhodný mechanismu, který ovlivňuje výsledky inteligentních hráčů. (Často se užívá termín „příroda“ => vyplývá z častých praktických aplikací teorie her pro výběr strategií hráče v závislosti na očekávaném počasí, klimatických podmínkách alpo. V takovém případě se pak mluví o hrách s přírodou)

3.5. Teorie her – konflikt inteligentních hráčů, záleží jim na výsledku

Teorie rozhodování – proti neinteligentnímu hráči (příroda), nezáleží na výsledku

„inteligentní hráč“ – hráči, kteří jsou na výsledku hry zainteresováni

4. Co je podstatou modelů teorie rozhodování? Uveďte a stručně popište komponenty těchto modelů.

4.1. Cílem je volba nejlepšího rozhodnutí

4.2. Komponenty:

Alternativy rozhodnutí, stavy okolností, rozhodovací kritérium, vektor rizika (je-li znám)

5. Odlište případy rozhodování za jistoty, za úplné nejistoty a za rizika. Ke každému případu uveďte praktický příklad.

5.1. Rozhodování za jistoty – ppts realizace jistého stavu okolností je rovna 1 a ppts ostatních stavů okolností se rovná 0

Rozhodování za rizika – ppts realizace stavů okolností jsou odhadovány či známy

Rozhodování za úplné nejistoty – ppts realizace stavů okolností jsou neznámé nebo je za neznámé považujeme

6. Co je to rozhodovací tabulka a rozhodovací strom? Jaké informace obsahují?

6.1. Rozhodovací tabulka – jedná se o maticovou formou zápisu rozhodovacího modelu; = nazývá se matice rozměru m x n (jestliže je m alternativ a n stavů okolností), jejímž prvky jsou jednotlivé výplaty v_ij

		Stavy okolností
		S1	S2	…	Sn
Alternativy	A1	v11	v12	…	v1n
	A2	v21	v22	…	v2n
	…	…	…	…	…
	An	vm1	vm2	…	vmn

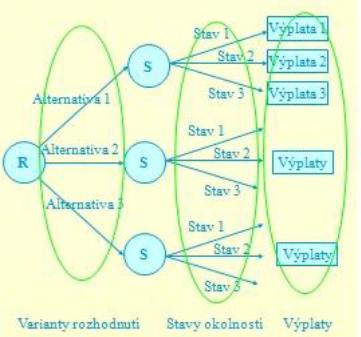
6.2. Rozhodovací strom – představují zobrazení struktury rozhodovacího procesu pomocí prostředků teorie grafů, pomocí stromů. Obsahují uzly a hrany zobrazující postup rozhodování