
- •Часть 1
- •Тема 1.9. Комплексные числа………………………………………………….…61
- •Список использованной и рекомендуемой литературы:
- •Раздел 1. Элементы теории множеств, векторной алгебры и аналитической геометрии. Вещественные числа
- •Тема 1.1. Элементы линейной алгебры
- •Матрицы и определители. Линейные операции над матрицами
- •1.1.2. Ранг матрицы
- •1.1.3. Методы решения систем линейных алгебраических уравнений
- •Для решения произвольных слау применяется метод Гаусса. Сущность метода состоит в том, что расширенная матрица слау приводится к ступенчатому виду. Метод Гаусса решения систем линейных уравнений.
- •Вопросы для самопроверки
- •Тема 1.2. Элементы векторной алгебры
- •1.2.1. Векторы, операции над векторами. Декартов базис
- •1.2.2. Скалярное произведение векторов
- •1.2.3. Векторное произведение векторов
- •1.2.4. Смешанное произведение трех векторов
- •Тема 1.3. Прямая и плоскость
- •1.3.1. Различные виды уравнения плоскости
- •1.3.2. Различные виды уравнения прямой в пространстве
- •1.3.3. Задачи, относящиеся к плоскостям
- •1.3.4. Задачи, относящиеся к прямой в пространстве
- •1.3.5. Взаимное расположение прямой и плоскости
- •1.3.6. Уравнение прямой линии на плоскости
- •Вопросы для самопроверки:
- •Тема 1.4. Преобразование координат на плоскости. Элементарная теория линий второго порядка
- •Вопросы для самопроверки
- •Тема 1.5. Некоторые сведения о линейных векторных пространствах. Собственные числа и собственные векторы
- •1.5.1. Векторные пространства и их преобразования
- •1.5.2. Собственные числа и собственные векторы матрицы линейного преобразования (оператора)
- •Вопросы для самопроверки
- •Тема 1. 6 . Квадратичные формы. Приведение к каноническому виду уравнений линии и поверхности второго порядка
- •1.6.1. Уравнения центральных поверхностей второго порядка
- •1.6.2. Нецентральные поверхности
- •1.6.3. Плоскости
- •Вопросы для самопроверки
- •Тема 1.7. Множества. Вещественные числа
- •1.7.1. Алгебраические свойства вещественных чисел
- •1.7.2. Отношение порядка На множестве вещественных чисел вводится отношение порядка , т.Е. , которое удовлетворяет следующим аксиомам:
- •1.7.3. Представление (модель) вещественного числа
- •1.7.4. Решение простейших неравенств с модулем
- •1.7.5. Открытые и замкнутые множества
- •1.7.6. Принципы существования предельной точки (Вейерштрасс)
- •Тема 1.8. Элементы теории пределов. Бесконечные функции
- •1.8.1. Определение предела в терминах окресностей
- •1.8.2. Общие свойства конечного предела
- •1.8.3. Бесконечно малые функции и их свойства
- •1.8.4. Представление функции, имеющей конечный предел
- •1.8.5. Свойства функций имеющих конечный предел в точке а
- •1.8.6. Бесконечно большие функции и их свойства
- •1.8.7. Числовые последовательности
- •Предел последовательности
- •1.8.9. Критерии существования предела последовательности
- •Тема 1.9. Комплексные числа
- •1.9.1. Понятие комплексного числа
- •1.9.2. Геометрическая интерпретация комплексного числа
- •1.9.3. Модуль комплексного числа
- •1.9.4. Сложение и умножение комплексных чисел
- •1.9.5. Вычитание и деление комплексных чисел
- •1.9.6. Тригонометрическая форма комплексного числа
- •1.9.7. Свойства модуля и аргумента комплексного числа
- •1.9.8. Возведение в степень и извлечение корня
- •1.9.9. Квадратное уравнение с комплексным неизвестным
- •Раздел 2. Дифференциальное и интегральное исчисление
- •Тема 2.1. Понятия о функции одной переменной. Предел и непрерывность функции
- •2.1.1. Свойства предела функции. Односторонние пределы
- •2.1.2. «Замечательные» пределы. Применение пределов в экономике
- •Тема 2.2. Дифференциальное исчисление функции одной переменной. Производная функции
- •Тема 2.3. Дифференциал функции
- •Тема 2.4. Производные высших порядков
- •Тема 2.5. Исследование функции. Формула Лагранжа
- •2.5.1. Необходимые и достаточные условия экстремума функции
- •2.5.2. Выпуклость, вогнутость и точки перегиба функции
- •2.5.3. Функция полезности
- •Раздел 3. Функция нескольких переменных Тема 3.1. Основные понятия функции нескольких переменных
- •Тема 3.2. Частные производные
- •Тема 3.3. Дифференциал функции двух переменных
- •Тема 3.4. Производная по направлению
- •Тема 3.5. Экстремум функции двух переменных
- •Упражнения
- •Раздел 4. Интегральное исчисление функции одной переменной Тема 4.1.Первообразная. Неопределенный интеграл
- •Тема 4.2.Методы интегрирования
- •4.2.1. Замена переменной в неопределенном интеграле
- •4.2.2. Формула интегрирования по частям
- •Интегрированне рациональной дроби
- •Интегрирование простейших дробей
- •Интегрирование выражений содержащих тригонометрические функции
- •4.2.6. Интегрирование иррациональных выражений
- •Тема 4.3. Определенный интеграл
- •4.3.1. Свойства и геометрический смысл определенного интеграла
- •4.3.2. Определенный интеграл как функция верхнего предела. Формула Ньютона-Лейбница
- •4.3.3. Несобственные интегралы с бесконечными пределами
- •Упражнения
- •4.3.4. Вычисление площадей плоских фигур
- •4.3.5. Определение длины кривой. Дифференциал кривой
- •Раздел 5. Обыкновенные дифференциальные уравнения Тема 5.1. Дифференциальные уравнения первого порядка
- •5.1.1. Дифференциальные уравнения с разделяющимися переменными
- •5.1.2. Линейные дифференциальные уравнения
- •5.1.3. Динамическая модель устойчивости рынка Вальраса
- •5.1.4. Линейные дифференциальные уравнения первого порядка с переменными коэффициентами
- •Упражнения
- •Раздел 6. Ряды и интеграл Фурье Основные сведения
- •Тема 6.1. Числовые ряды
- •6.1.1. Условие сходимости положительного числового ряда
- •Тема 6.2. Тригонометрический ряд. Ряд Фурье
- •6.2.1.Достаточные признаки разложимости функции в ряд Фурье
- •6.2.2. Ряды Фурье для четных и нечетных функций
- •6.2.3. Ряд Фурье по любой ортогональной системе функций
- •Тема 6.3. Комплексная форма ряда Фурье. Задача о колебании струны
- •Задача о колебании струны
- •Тема 6.4. Интеграл Фурье
- •6.4.1. Интеграл Фурье для четной и нечетной функции
- •6.4.2. Комплексная форма интеграла Фурье
- •6.4.3. Формулы дискретного преобразования Фурье
- •Раздел 7. Представление функции интегралом Фурье
- •Тема 7.1. Проверка условий представимости
- •7.1.1. Представление функции интегралом Фурье
- •7.1.2. Интеграл Фурье в комплексной форме
- •Тема 7.2. Представление функции полиномом Лежандра
- •7.2.1. Основные сведения
- •7.2.2. Преобразование функции
- •7.2.3. Вычисление коэффициентов ряда
- •Раздел 8. Дискретные преобразования Фурье
- •Тема 8.1. Прямое преобразование
- •Тема 8.2. Обратное преобразование
- •Раздел 9. Элементы теории вероятностей Тема 9.1. Комбинаторные формулы
- •Тема 9.2. Случайный эксперимент, элементарные исходы, события. Диаграммы Венна
- •Тема 9.3. Вероятностное пространство. Случай конечного или счетного числа исходов
- •9.3.1. Классическое определение вероятности
- •9.3.2. Статистическое определение вероятности
- •9.3.3. Непрерывное вероятностное пространство
- •9.3.4. Геометрическая вероятность
- •9.3.5. Формулы сложения вероятностей
- •9.3.6. Условная вероятность. Независимые события. Умножение вероятностей
- •Тема 9.4. Формула полной вероятности
- •9.4.1. Формула Байеса
- •9.4.2. Повторные независимые испытания. Формула Бернулли
- •Тема 9.5. Законы распределения случайной величины
- •9.5.1. Биноминальное распределение случайной величины
- •9.5.2. Асимптотические формулы Бернулли. Случайная величина, распределенная по закону Пуассона
- •9.5.3. Локальная и интегральная формулы Лапласа
- •Тема 9.6. Дискретные случайные величины
- •9.6.1. Зависимость и независимость двух случайных величин
- •9.6.2. Математическое ожидание случайной величины
- •9.6.3. Дисперсия случайной величины
- •Свойства дисперсии:
- •Тема 9.7. Непрерывные случайные величины. Плотность и функция распределения случаной величины
- •9.7.1. Математическое ожидание случайной величины
- •9.7.2. Дисперсия случайной величины
- •9.7.3. Нормальное распределение
- •Раздел 10. Элементы математической статистики Тема 10.1. Задачи математической статистики
- •10.1.1. Выборочный метод. Генеральная совокупность
- •10.1.2. Вариационный ряд
- •10.1.3. Точечные оценки параметров генеральной совокупности
- •Тема 10.2. Интервальные оценки
- •10.2.1. Понятие интервальной оценки
- •10.2.2. Доверительный интервал для математического ожидания нормального распределения при известной дисперсии
- •10.2.3. Доверительный интервал для математического ожидания нормального распределения при неизвестной дисперсии
- •10.2.4. Доверительный интервал дисперсии нормального распределения
- •Тема 10.3. Задачи статистической проверки гипотез
- •10.3.1. Основные понятия и статистическая проверка гипотез
- •10.3.2. Проверка статистической гипотезы о математическом ожидании нормального распределения при известной дисперсии
- •10.3.3. Проверка гипотезы о равенстве дисперсий
- •10.3.4. Проверка статистической значимости выборочного коэффициента корреляции
- •Тема 10.4. Сравнительная оценка параметров эмпирического и нормального распределений. Критерий Пирсона «хи» квадрат
- •Данные распределения среднемесячной заработной платы:
1.8.5. Свойства функций имеющих конечный предел в точке а
Пусть
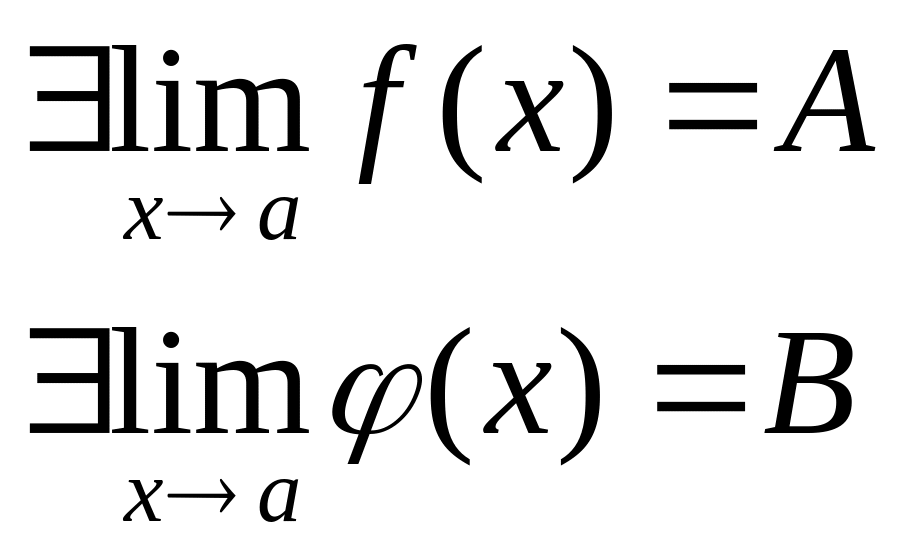 ,
тогда:
,
тогда:
Существует предел алгебраической суммы этих функций, равный алгебраической сумме этих пределов
![]()
Существует предел произведения функций произведение пределов
![]()
Если предел знаменателя неравен 0 и B неравно 0 то

Следствие
Из 1 и 2 следует, что константы можно выносить за знак предела
![]()
1.8.6. Бесконечно большие функции и их свойства
Определение: Функция называется бесконечно большой в точке а, если ее предел в этой точке равен бесконечности.
![]()
Свойства:
Пусть
и
![]() -
бесконечно большие функции в точке а.
-
бесконечно большие функции в точке а.
Тогда справедливы следующие утверждения:
Произведение двух бесконечно больших функций – бесконечно большая функция.
![]()
Произведение бесконечно больших на функцию, имеющую отличный от нуля предел - бесконечно большая.
![]()
Функция, обратная величине бесконечно большой – есть бесконечно малая, и наоборот.
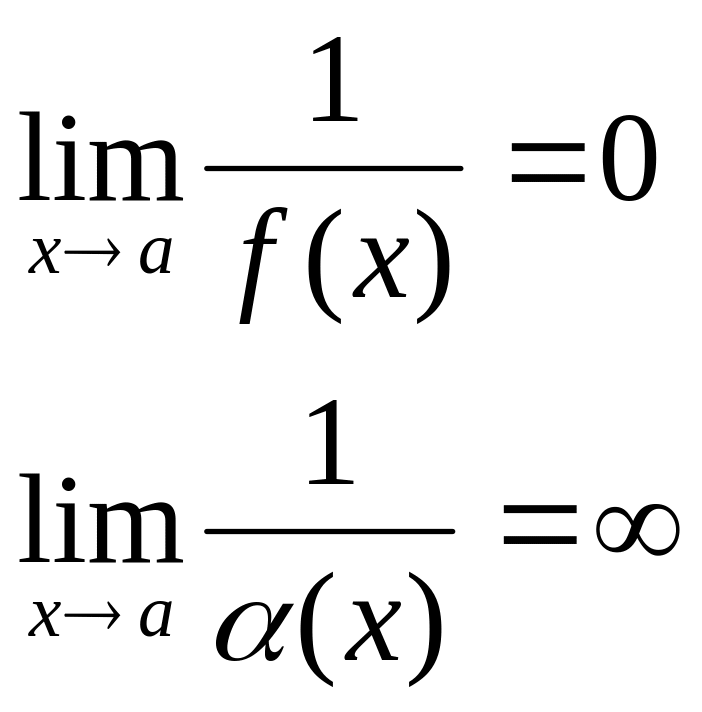
Д![]() оказательство
2):
оказательство
2):
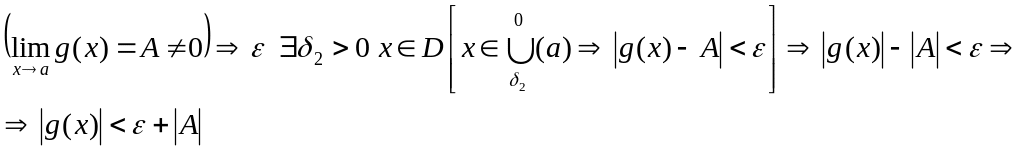
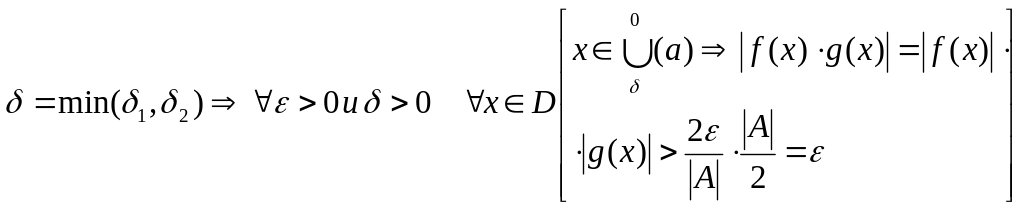
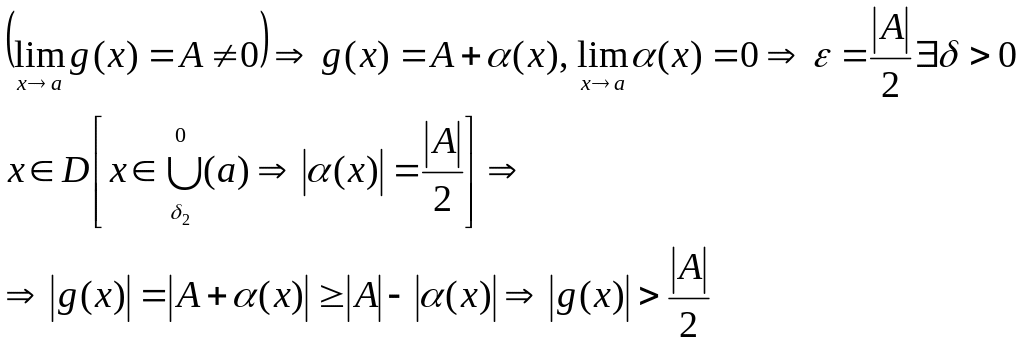
Доказательство 3):
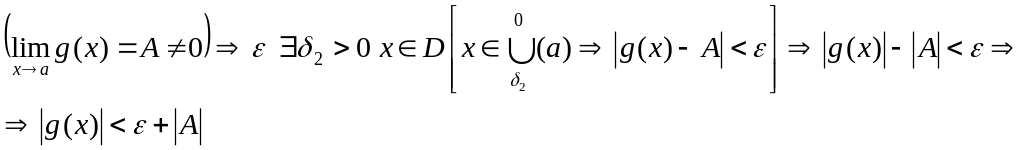
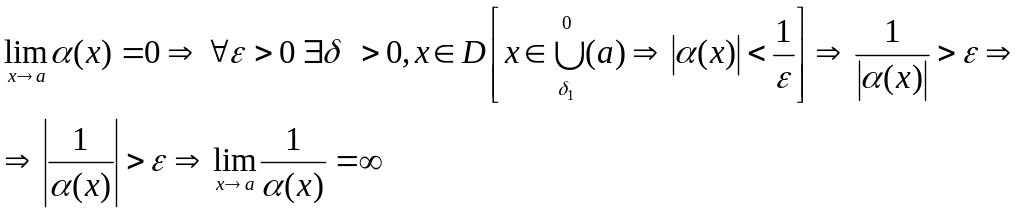
1.8.7. Числовые последовательности
Задача, по которой каждому N числу, ставится в соответствие единственное вещественное число – называется числовой последовательностью.
Числовая последовательность – функция натурального аргумента.
Обозначается:
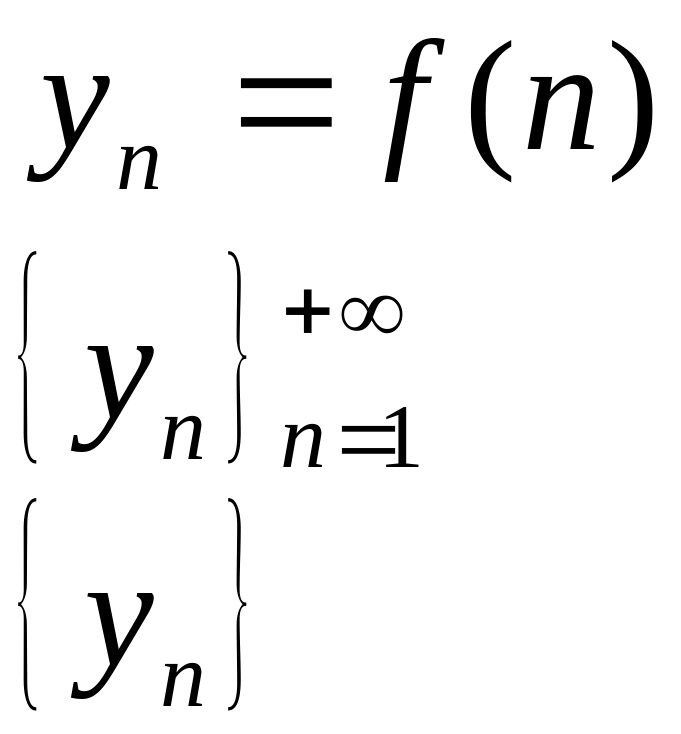
Последовательность, множество значений которой состоит из одного числа – стационарная.
Так как числовая последовательность – не симметричное множество, то для него не существует понятия четности, нечетности, периодичности. Зато сохраняются свойства, связанные с упорядоченностью.
Свойства:
Ограниченность.
последовательность
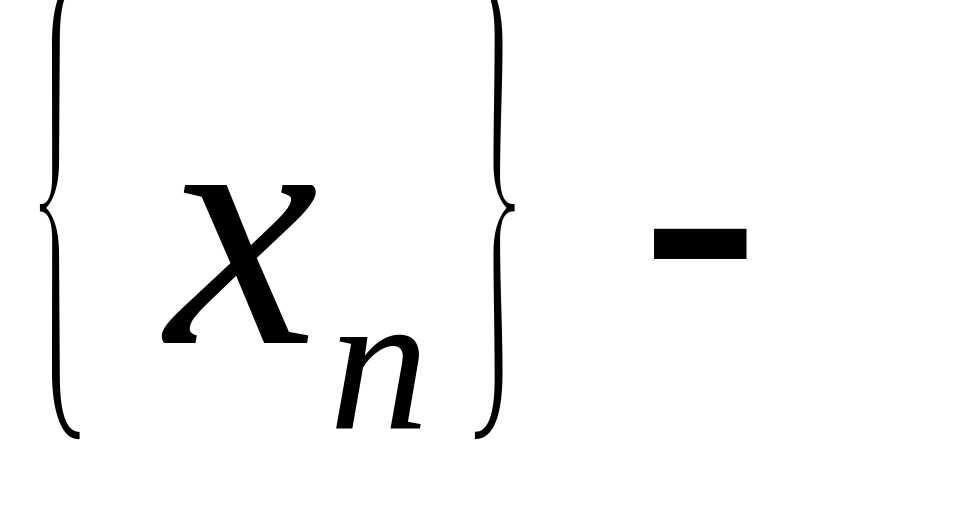 ограничена
сверху, если
ограничена
сверху, если
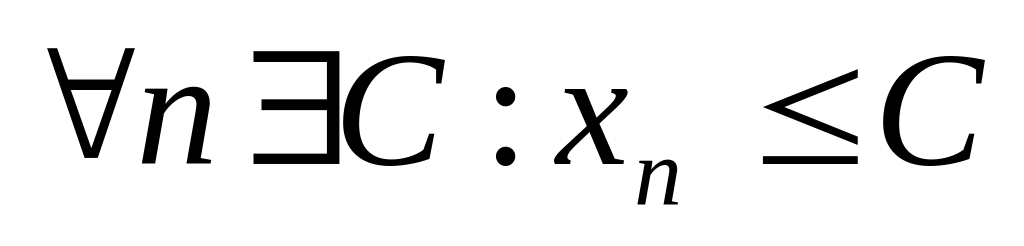
последовательность ограничена снизу, если
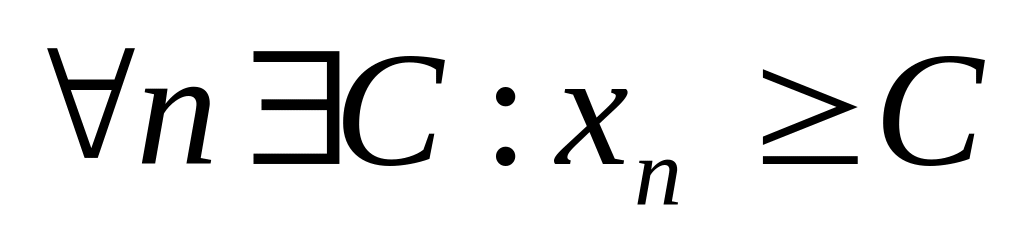
последовательность ограничена, если

Монотонность.
последовательность возрастает, если

последовательность убывает, если

последовательность не убывает, если

последовательность не возрастает, если

Предел последовательности
Так
как натуральные числа имеют одну только
бесконечность, то для числовой
последовательности существует
![]()
![]()
Замечания:
А может быть конечным или бесконечным
Если последовательность имеет конечный предел, то она называется сходящейся, а если нет – расходящейся.
Общие свойства сходящихся последовательностей аналогичны свойствам функций, имеющих конечный предел.
Арифметические свойства сходящихся последовательностей аналогичны свойствам функций, имеют конечный предел
Переход к пределам в неравенствах, для сходящихся последовательностей аналогичен функциям, имеющим конечный предел.
Определение бесконечно малых и бесконечно больших последовательностей и их свойства аналогичны соответствующим определениям и свойствам функции непрерывного аргумента.
1.8.9. Критерии существования предела последовательности
1. Критерии Коши (произведения последовательностей)
Для
существования предела последовательностей
необходимо
и достаточно, чтобы для любой..............![]()
![]()
Последовательность, для которой выполняется признак Коши – фундаментальная.
2. Критерий Вейерштрасса (монотонность последовательности):
а) неубывающие последовательности, ограниченные сверху, имеют предел
![]()
б) не возрастающие последовательности, ограниченные снизу, имеют предел.
Доказательство:
![]()
