Метод №2. Визначення широти із спостережень Сонця, проведених на значній віддалі від меридіану
У випадку, якщо годинний кут Сонця перевищує 1 годину, необхідно виконувати розрахунки за формулою, що виводиться нижче.
Запишемо формулу косинусів для сторін паралактичного трикутника (мал. 1):
(18)
(19)
(20)
Скористаємося також формулою синусів:
(21)
і формулою п’яти елементів для сторони
:
(22)
Підставимо (19) в (18):
(23)
З (22) виразимо
і підставимо його в (23):
(24)
В останній член правої частини (24) підставимо з (20):
Виконуючи перетворення, одержимо:
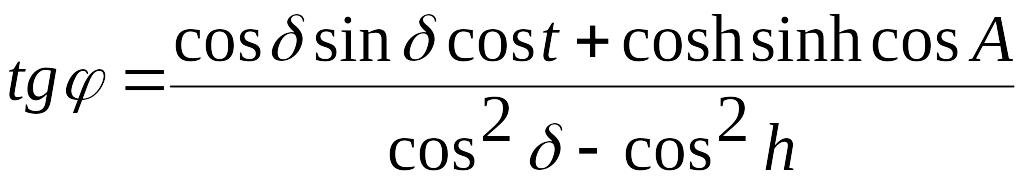
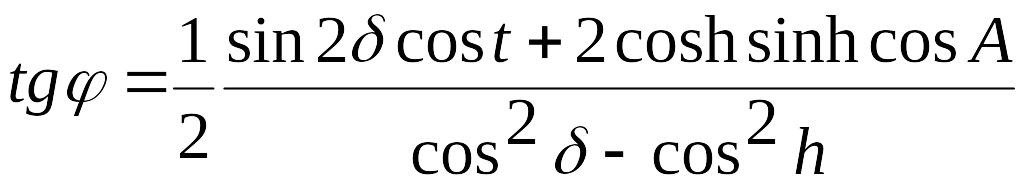(25)
Тепер з (21) визначимо
:
і підставимо його значення в (25):
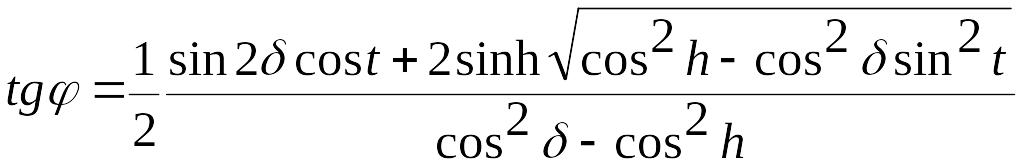(26)
Одержана формула дозволяє визначити географічну широту для довільних моментів часу, якщо відома висота, схилення і годинний кут Сонця. Як вже зазначалося, точність результатів цього методу є цілком задовільною для розв’язування учбових задач. Необхідно лише мати на увазі, що за таких умов спостережень, коли висота Сонця за модулем близька до його схилення, знаменник в (26) прямує до нуля, і використання формули призводить до грубих помилок.
Іх. Акцентні терміни
Паралактичний трикутник
Формула п’яти елементів
Годинний кут t.
Екліптична широта .
Географічна широта.
Моменту кульмінації
Висотою сонця
Громадянський час
Рівняння часу
Кульмінація світила
Рефракція
Добовий паралакс
Х. Література
Бакулин П.И. и др. Курс общей астрономи. – М.: Наука, 1983.
Блажко С.Н. Курс практической астрономи. – М.:Наука, 1979.
Хі. Додатки
Приведення на меридіан
для годинних кутів
при різних наближених значеннях
і
.
|
49 |
50 |
51 |
52 |
|
49 |
50 |
51 |
52 |
0 +1 2 3 4 +5 6 7 8 9 +10 11 12 13 14 +15 16 17 18 19 +20 21 22 23 24
|
- 11,4 11,5 11,7 11,9 12,1 - 12,3 12,5 12,7 12,7 13,2 -13,4 13,1 13,9 14,2 14,5 -14,8 15,1 15,4 15,8 16,2 -16,6 17,0 17,4 17,0 18,4 |
- 11,0 11,1 11,3 11,5 11,6 - 11,7 12,0 12,2 12,4 12,6 -12,9 13,1 13,3 13,6 13,9 -14,1 14,4 14,7 15,0 15,4 -15,7 16,1 16,5 17,0 17,4 |
- 10,6 10,7 10,9 11,0 11,2 - 11,4 11,6 11,7 11,9 12,1 -12,3 12,5 12,8 13,0 13,2 -13,5 13,8 14,0 14,3 14,6 -15,0 15,3 15,7 16,0 16,5 |
- 10,2 10,3 10,5 10,6 10,8 - 11,0 11,6 11,1 11,5 11,6 -11,8 12,0 12,2 12,4 12,7 -12,9 13,1 13,4 13,7 13,9 -14,2 14,5 14,9 15,2 15,6 |
0 - 1 2 3 4 - 5 6 7 8 9 - 10 11 12 13 14 - 15 16 17 18 19 - 20 21 22 23 24
|
- 11,4 11,2 11,0 10,9 10,7 - 10,6 10,4 10,3 10,1 10,1 -9,9 9,7 9,6 9,5 9,3 - 9,2 9,1 9,0 8,9 8,8 - 8,6 8,5 8,4 8,3 8,2 |
- 11,0 10,8 10,7 10,5 10,4 - 10,2 10,1 9,9 9,8 9,7 -9,6 9,4 9,3 9,2 9,2 - 9,0 8,8 8,7 8,6 8,5 - 8,4 8,3 8,2 8,1 8,0 |
- 10,6 10,4 10,3 10,2 10,0 - 9,9 9,8 9,6 9,5 9,4 -9,3 9,1 9,0 8,9 8,8 - 8,7 8,6 8,5 8,4 8,3 - 8,2 8,1 8,0 7,9 7,8 |
- 10,2 10,1 9,9 9,8 9,7 - 9,6 9,4 9,3 9,2 9,1 -9,0 8,9 8,8 8,7 8,5 - 8,4 8,3 8,2 8,1 8,0 - 8,0 7,9 7,8 7,7 7,6 |
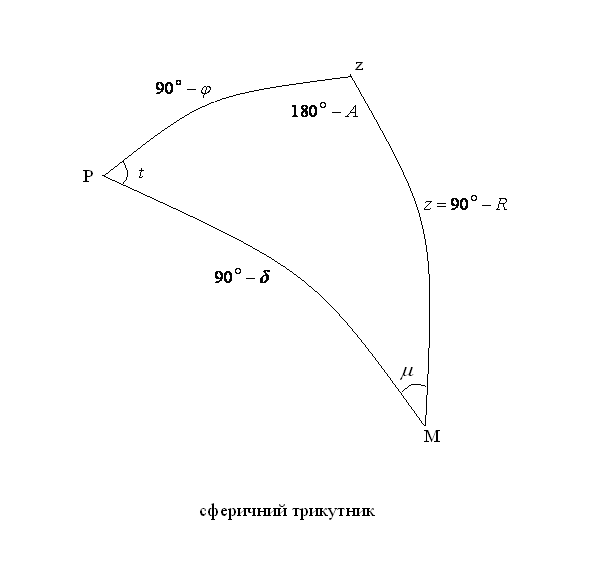
Мал. 1. Математичне представлення сферичного трикутника.
Мал. 1. Географічне представлення поясів за широтою.