Ограничения на параметры системы, описываемой классической физикой

Классическая физика применима, когда несущественны интерференция и дифракция частиц, приводящие к квантованию энергии и дискретности фазового пространства.

1. Высокие температуры, при которых несущественна дискретность спектра квантовых состояний:

, (П.1.5)

где – уровень энергии системы.

Для частицы в кубическом ящике со стороной L согласно (П.1.3)

.

Допустимые значения проекции импульса

,

и энергии частицы

.

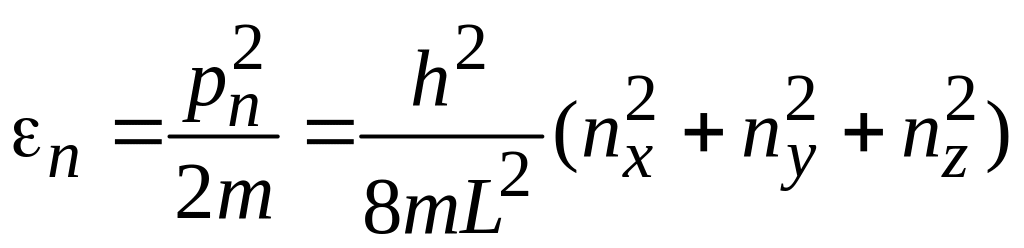Из (П.1.5) получаем

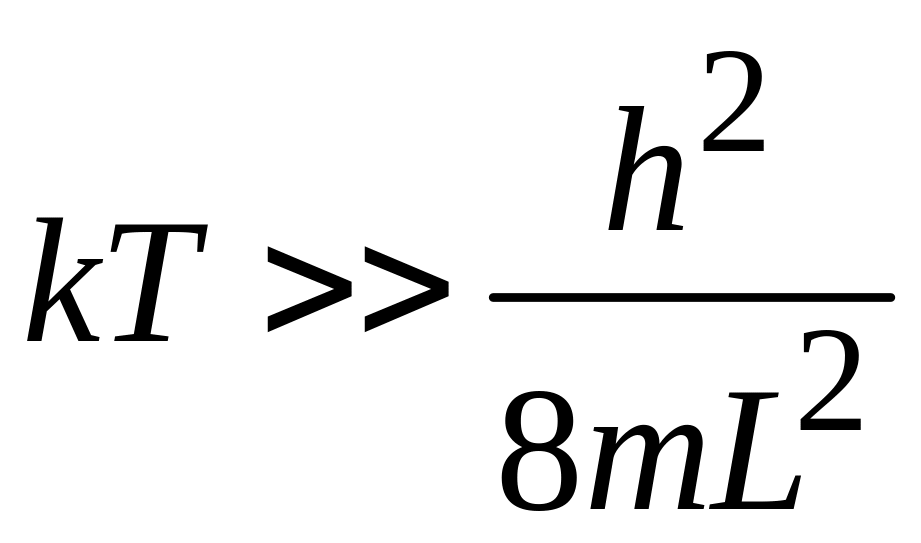. (П.1.6)

При большом размере системы и высокой температуре квантование энергии несущественно.

2. Большое расстояние r между частицами по сравнению с длиной волны де Бройля

. (П.1.7)

Согласно распределению Максвелла наиболее вероятная скорость частицы (2.45)

,

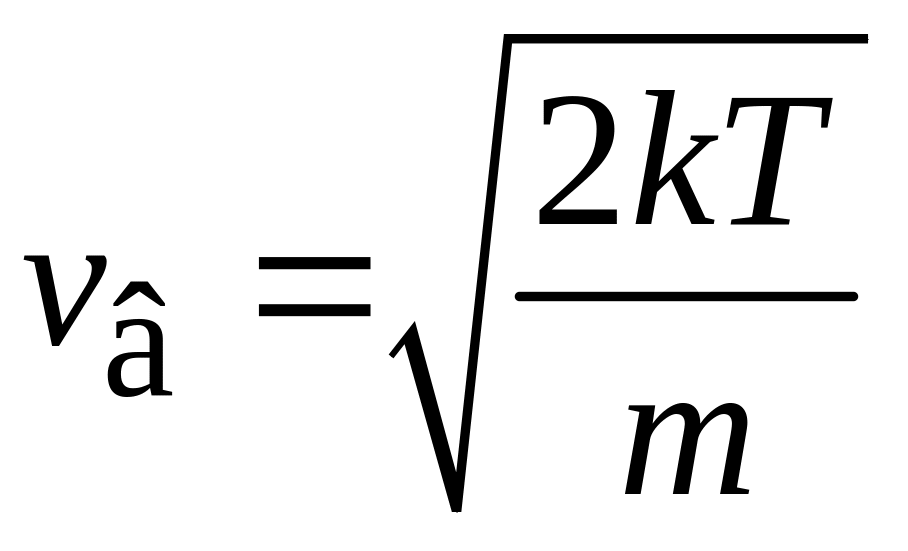тогда наиболее вероятный импульс

.

Из (1.7)

.

получаем наиболее вероятную длину волны де Бройля частицы

.

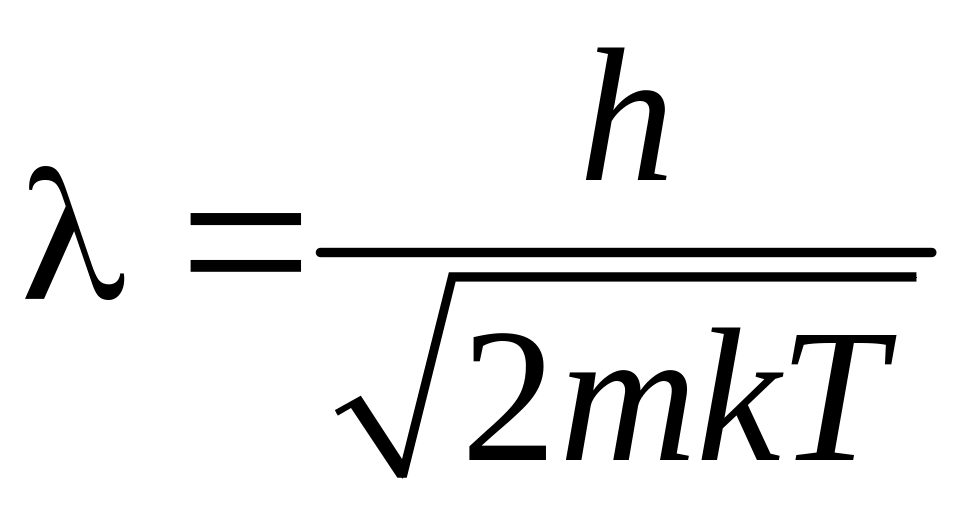Среднее расстояние между частицами газа выражаем через объем сосуда V и число частиц N

,

откуда

,

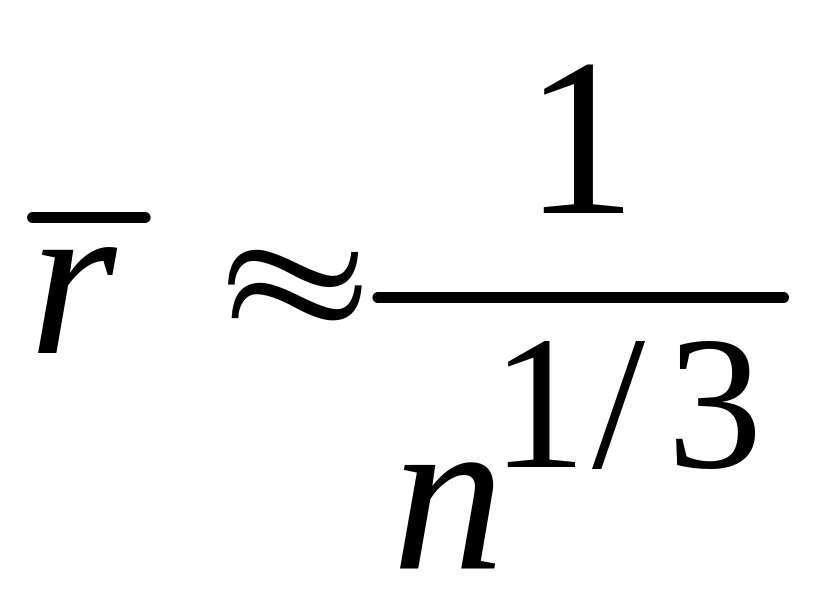где – концентрация частиц. Условие (П.1.7) принимает вид

. (П.1.8)

Классическая теория идеального газа выполняется при достаточно малых концентрациях, высоких температурах и не слишком малых массах частиц.

Сопоставляем (П.1.8) с химическим потенциалом (2.62а)

,

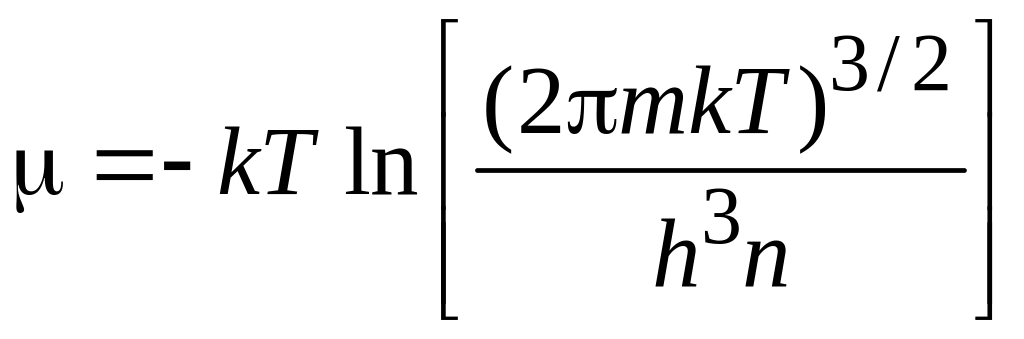получаем

 < 0.

В области применимости классической теории химический потенциал отрицателен.

Для гелия при нормальных условиях находим

,

,

,

,

,

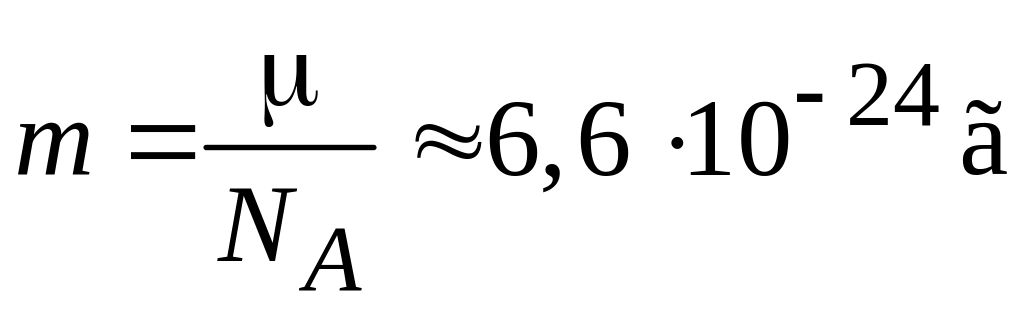выполняется и классическая физика применима.

Для электронов в металле при нормальной температуре

_.

Расстояние между узлами кристаллической решетки

см.

Условие нарушается. Классическая физика не применима для электронного газа в металле.

В полупроводниках длина волны де Бройля электрона при нормальной температуре и ширина запрещенной зоны

Т = 300 К	Ge	Si	GaAs	InSb
λ, мкм	610–3	7,710–3	2,910–2	6,710–2
Eg, эВ	0,67	1,12	1,42	0,17

В узкозонных полупроводниках с шириной запрещенной зоны , например InSb, InAs, концентрация электронов проводимости велика, расстояние r между электронами достигает микронных размеров, условие классического описания нарушается.

3. Большой объем фазового пространства, приходящийся на частицу, по сравнению с постоянной Планка

. (П.1.9)

Выразим флуктуации через параметры системы. По теореме о распределении энергии по степеням свободы средняя кинетическая энергия одномерного движения узла кристаллической решетки

,

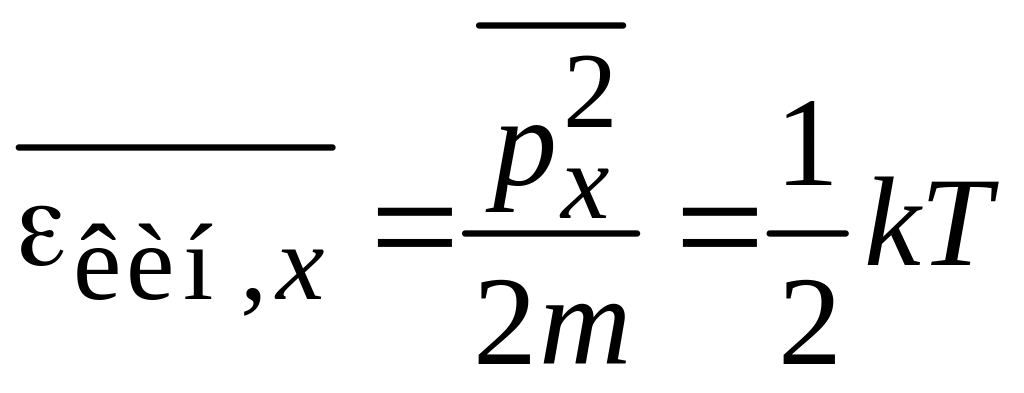тогда

.

Тепловая флуктуация проекции импульса с учетом равна

.

Средняя потенциальная энергия упругих колебаний по теореме о распределении энергии по степеням свободы

,

тогда

.

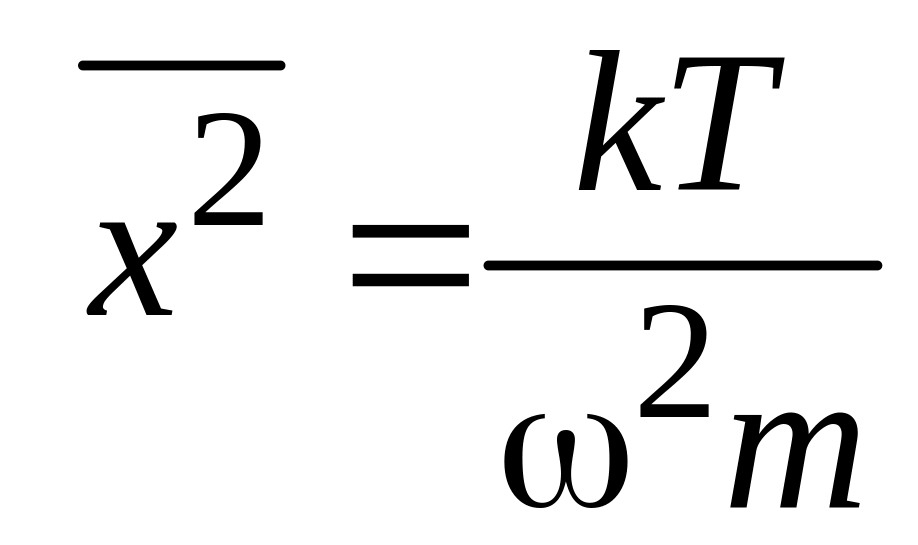где  – круговая частота собственных колебаний узлов кристалла. Чем прочнее кристалл, тем больше частота:

медь – ,

алмаз – .

Тепловая флуктуация координаты узла с учетом равна

.

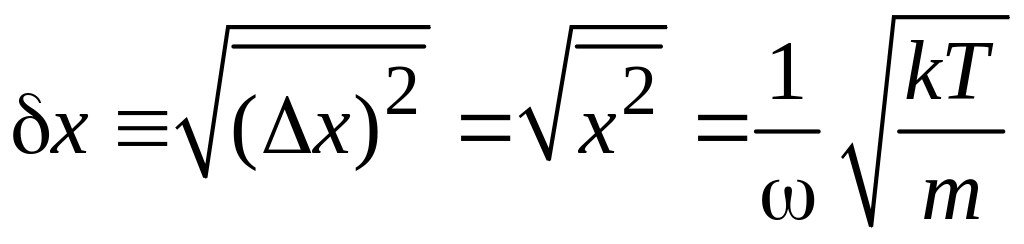В результате

.

Условие (П.1.9) получает вид

. (П.1.10)

Чем прочнее кристалл и ниже температура, тем меньше согласие с классической теорией. Классическая физика не применима для прочных кристаллов при низкой температуре.

Для систем, нарушающих хотя бы одно из полученных условий, необходимо использовать квантовую статистическую физику.