7. Складываем (6.128) и (6.130)
.
(6.133)
8. Дифференцируем раз (6.105)
,
получаем
.
По формуле Лейбница
,
тогда
.
Результат умножаем на и сравниваем с (6.118)
,
находим
.
(6.134)
9.
Умножаем на
выражение (6.132)
,
получаем
.
(6.132а)
Умножаем
на
(6.134), тогда
.
(6.134а)
Вычитаем (6.134а) из (6.132а) и находим
.
(6.135)
10.
Исключаем
из (6.135) и из выражения (6.127)
,
получаем
.
(6.136)
11.
Исключаем
из (6.133), (6.134) и учитываем (6.135). Получаем
соотношение с одинаковыми верхними
индексами
.
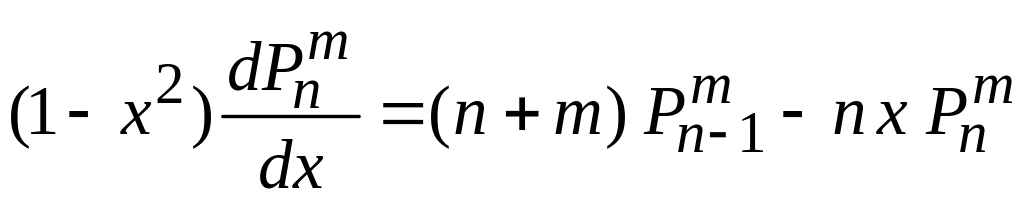(6.137)
12.
Из (6.137) и (6.127) исключаем
и находим
.
(6.140)
Интегралы с полиномами лежандра
1.
.
(П.6.12)
Доказательство:
Упрощаем интеграл, используя рекуррентное соотношение (6.125)
,
тогда
.
Интегралы вычисляем при помощи условия ортонормированности (6.123)
.
Тогда
,
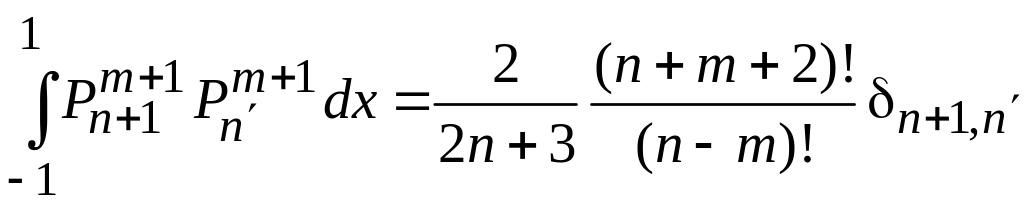где
.
Аналогично находим
,
где
.
В результате получаем (П.6.12).
2. Доказать условия ортогональности (6.123) и (6.124)
,
;
,
.
Доказательство:
Используем
уравнение Лежандра (6.115) для
и
:
,
.
Первое уравнение умножаем на , второе – на и взаимно вычитаем результаты.
Упрощаем первые два слагаемые
.
Из уравнений получаем
.
Интегрируем по интервалу . Первое слагаемое, вычисленное по формуле
,
дает нуль. Находим
.
При
,
получаем (6.123).
При
,
получаем (6.124).
3. Доказать условие нормировки полиномов Лежандра (6.112)
.
Доказательство:
Подставляем (6.96)
в интеграл и находим
.
Интегрируем по частям, полагая
,
.
Свободное слагаемое дает нуль на обоих пределах.
После n-кратного интегрирования по частям получаем
,
где учтено
.
Используем (П.3.9)
,
и получаем условие нормировки полиномов Лежандра (6.112).
4. Доказать условие нормировки присоединенных функций Лежандра (6.123)
.
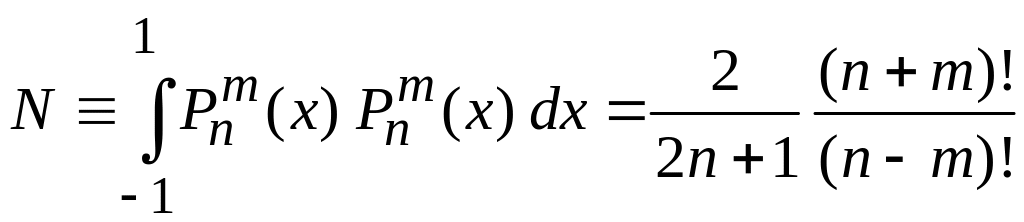Доказательство:
В интеграл подставляем формулы Родрига (6.117) и (6.119)
,
,
получаем
.
Интегрируем по частям, полагая
,
,
свободные
слагаемые дают нули. Повторяя интегрирование
раз, получаем
.
Интеграл вычислен в предыдущем примере
,
в результате
.
Полиномы Чебышева первого рода
,
;
– порядок полинома.
Имеют
наименьшее отклонение от нуля на
интервале
и максимальное отклонение за пределами
этого интервала по сравнению с другими
полиномами того же порядка.
Используются для интерполирования и аппроксимации функций. Интерполирование – построение функции, проходящей через заданные точки. Аппроксимация – замена сложной функции более простой функцией, совпадающей с исходной в ряде точек.
Полиномы исследовал Пафнутий Львович Чебышев (нем. Tschebyschew) в 1854 г.