
- •2)Риман интегралын есептеу әдістері.Ньютон-Лейбниц формуласы.
- •3)Риман интегралы.Геометриялық және механикалық есептеулерде қолданылуы.
- •4)Көп айнымалы ф-я(каф), оның шегі, үзіліссіздігі.
- •7)Толық дифференциал формасының сақталу қасиеті,(инварианттылығы)
- •8) Ка күрделі ф-ны дифференциалдау,толық туынды формасы
- •10)Кез-келген бағыт б/ша туынды ж/не градиент
- •15) Таңбалары тұрақты сандық қатардың жинақтылығының жеткілікті шарты,Даламбер, салыстыру,т.Б. Қатарларды салыстыру белгілері.
- •18)Функционалдық қатар.Дәрежелік қатардың жинақтылығы, Абель теоремасы.
- •19)Дәрежелік қатардың жинақтылық интервалы ж/не жин r радиусы, негізгі қасиеттері.
- •21)Кейбір элементар функцияның Тейлор қатарына жіктелінуі.
- •22)Екі еселі интеграл, ж/не оның қасиеттері.
- •Сурет 1
- •Полярлық координаталар
- •Сурет 8
- •Сурет 9
- •24)Екі еселі интегралдың кейбір геометриялық және механикалық қолданулары
- •27) Үш еселі интегралда айнымалыны алмастыру, жалпы жағдай
- •28) Үш еселі интегралды цилиндрлік ж/не сфералық коорд жүйесінде есептеу
- •2.6 Үш еселі интегралда сфералық координаталарға көшу
19)Дәрежелік қатардың жинақтылық интервалы ж/не жин r радиусы, негізгі қасиеттері.
(6.1)
I–анықтама.
(6.1) қатары
теңсіздігін қанағаттандыратын барлық
үшін жинақты болатын,ал теңсіздігін қанағаттандыратын барлық
үшін жинақсыз болатын.
саны бар болса, оны қатардың жинақтылық
радиусы д.а.Егер (6.1) қатары тек
нүктесінде жинақты болса, онда
теңсіздігін қанағаттандыратын барлық
үшін жинақсыз болатын.
саны бар болса, оны қатардың жинақтылық
радиусы д.а.Егер (6.1) қатары тек
нүктесінде жинақты болса, онда
 болады. Егер (6.1) қатары кез келген
нүктеде жинақты болса, онда
болады. Егер (6.1) қатары кез келген
нүктеде жинақты болса, онда
 болады. Енді дәрежелік қатардың жинақтылық
радиусын анықтау тәсіліне келейік.
болады. Енді дәрежелік қатардың жинақтылық
радиусын анықтау тәсіліне келейік.
2-теорема.
Егер (6.1) дәрежелік қатардың
 тізбегінің шектеулі немесе шектеусіз
шегі бар болса, онда жинақтылық радиусы
тізбегінің шектеулі немесе шектеусіз
шегі бар болса, онда жинақтылық радиусы
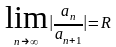 (6.3) формуласымен анықталады.
(6.3) формуласымен анықталады.
Дәлелдеу:
Айталық
 болсын. Алдымен,
болсын. Алдымен,
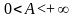 жағдайын қарастырайық. Кез келген
санын таңдап алайық және
жағдайын қарастырайық. Кез келген
санын таңдап алайық және
 сан қатарына Даламбер белгісін қолданайық.
Сонда
сан қатарына Даламбер белгісін қолданайық.
Сонда
 және
және болғандықтан,
болғандықтан,
 Даламбер белгісіне сәйкес, егер
Даламбер белгісіне сәйкес, егер
 болса, қатар абсолютті жинақты болады:
ал
болса, қатар абсолютті жинақты болады:
ал
 болса, қатар жинақсыз болады. Демек,
болса, қатар жинақсыз болады. Демек,
 Егер
Егер
 болса кез келген
үшін
болса кез келген
үшін
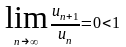 болады. Демек, кез келген
үшін қатар жинақты, яғни
болады. Демек, кез келген
үшін қатар жинақты, яғни
 болады. Егер
болады. Егер
 болса, онда кез келген
үшін
болса, онда кез келген
үшін
 яғни қатар кез келген
үшін жинақсыз болады. Бұл жағдайда
болады.
яғни қатар кез келген
үшін жинақсыз болады. Бұл жағдайда
болады.
3–теорема.
Айталық
 тізбегінің шектеулі шегі бар немесе
шексіз шегі болсын. Сонда қатардың
жинақтылық радиусы
тізбегінің шектеулі шегі бар немесе
шексіз шегі болсын. Сонда қатардың
жинақтылық радиусы
 формуласымен анықталады.
формуласымен анықталады.
I
–мысал.
 қатарының
жинақтылық облысын көрсетейік.
қатарының
жинақтылық облысын көрсетейік.
Шешуі:
Мұнда
 және
және
 .
Сонда
.
Сонда

 Сондықтан, қатар (-1;1) аралығында
жинақты болады. Сонымен бірге
Сондықтан, қатар (-1;1) аралығында
жинақты болады. Сонымен бірге
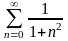 сан қатары жинақты болғандықтан, берілген
қатар
сан қатары жинақты болғандықтан, берілген
қатар
 нүкелерінде де абсолютті жинақты болады.
Соңында берілген қатар
нүкелерінде де абсолютті жинақты болады.
Соңында берілген қатар
 кесіндінде абсолютті жинақты, ал барлық
кесіндінде абсолютті жинақты, ал барлық теңсіздігін қанағатандыратын нүктелерде
үшін жинақсыз болатынын аламыз.
теңсіздігін қанағатандыратын нүктелерде
үшін жинақсыз болатынын аламыз.
2.Дәрежелік
қатарлардың қасиеттері. Айталық
функциясы
 (6.5)
(6.5)
Қатарының
қосындысы және
 жинақтылық аралығы болсын.
жинақтылық аралығы болсын.
Бұл жағдайда, және аралығында дәрежелік қатарға жіктеледі немесе -тің дәрежелері бойынша қатарға жіктеледі деп айтады.
Енді дәрежелік қатардың қасиеттері туралы екі теореманы дәлелдеусіз келтірейік.
4-
теорема. Егер
функциясы
аралығында (6.5) түрдегі дәрежелік қатарға
жіктелсе, онда қатар бұл аралықта
дифференциалданады және оның туындысы
(6.5) қатарды мүшелеп дифференциалдау
арқылы алынуы мүмкін, яғни

 , болады. Осы тәрізді
функциясының кез келген ретті туындысын
алуға болады. Бұл жағдайда, алынған
қатарлардың жинақтылық радиусы бастапқы
қатардың жинақтылық радиусына тең
болады.
, болады. Осы тәрізді
функциясының кез келген ретті туындысын
алуға болады. Бұл жағдайда, алынған
қатарлардың жинақтылық радиусы бастапқы
қатардың жинақтылық радиусына тең
болады.
5-
теорема. Егер
функциясы
аралығында дәрежелік қатарға жіктелетін
болса, онда функция бұл аралықта
интегралданады және функция интегралын
(6.5) қатарын мүшелеп интегралдау арқылы
алу мүмкін болады, яғни
 болса, онда
болса, онда

=
Ал,
 болғанда (6.5) қатарды
болғанда (6.5) қатарды
 кесіндісінде интегралдаудың нәтижесінде,
жаңа
кесіндісінде интегралдаудың нәтижесінде,
жаңа
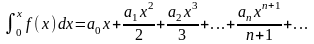
қатар алынады. Бұл қатардың жинақтылық аралығы да аралығы болады. Қатарларды дифференциялдау мен интегралдау қатарларды зерттеуде жиі қолданылады.
20)Тейлор
ж/не Маклорен қатарлары, Тейлор қатарына
жіктелудің қажетті ж/не жеткілікті
шарттары.Тейлор
қатары. Айталық
функциясы жинақтылық аралығы
болатын
 (7.1)дәрежелік қатарының қосындысы
болсын. Бұл жағдайда,
функциясы
нүктесінің төңірегінде дәрежелік
қатарға жіктеледі немесе
(7.1)дәрежелік қатарының қосындысы
болсын. Бұл жағдайда,
функциясы
нүктесінің төңірегінде дәрежелік
қатарға жіктеледі немесе
 -дің
дәрежелері бойынша жіктеледі дейді.
Енді
-дің
дәрежелері бойынша жіктеледі дейді.
Енді
 коэффициенттерін анықтайық. Бізге,
дәрежелік қатарды жинақтылық аралығында
үшелеп дифференциалдауға және нәтижесінде
алынатын қатардың жинақтылық аралығы
сол
аралығы болатыны белгілі. (7.1) теңбе-теңдікті
біртіндеп дифференциалдасақ, жинақтылық
аралығында жататын кез келген
үшін дұрыс болатын теңбе-теңдікті
аламыз. Демек,
коэффициенттерін анықтайық. Бізге,
дәрежелік қатарды жинақтылық аралығында
үшелеп дифференциалдауға және нәтижесінде
алынатын қатардың жинақтылық аралығы
сол
аралығы болатыны белгілі. (7.1) теңбе-теңдікті
біртіндеп дифференциалдасақ, жинақтылық
аралығында жататын кез келген
үшін дұрыс болатын теңбе-теңдікті
аламыз. Демек,
 болғандықтан
мұны біртіндеп дифференциалдасақ:
болғандықтан
мұны біртіндеп дифференциалдасақ:
 +
+




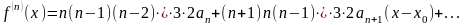 Бұл
өрнектердегі
десек,
Бұл
өрнектердегі
десек,


теңдіктерін
аламыз. Бұдан
 Анықталған коэффициенттердің мәндерін
(7.1) теңдігіне қойсақ,
Анықталған коэффициенттердің мәндерін
(7.1) теңдігіне қойсақ,


қатарын
аламыз. Демек,
функциясы
-дің
дәрежелері бойынша дәрежелік қатарға
жіктелсе, ол қатар
 (7.2) түрінде жазылады. Алынған қатарды
функциясы үшін Тейлор қатары д.а..
(7.2) түрінде жазылады. Алынған қатарды
функциясы үшін Тейлор қатары д.а..
Дербес
жағдайда,
болғанда (7.2) қатары мына түрге келеді:
 (7.3)
(7.3)
Бұл қатар функциясы үшін Маклорен қатары деп аталады. Сонымен, функциясы өрнегінің дәрежелері бойынша қатарға жіктелсе, бұл қатарды Тейлор қатары (егер болса, Маклорен қатары) дейді . Бұдан, егер функция өрнегі бойынша дәрежелік қатарға жіктелсе, онда ол функция нүктесінде барлық ретті жоғары туындылары бар, немесе нүктесінде шексіз дифференциалданады дейді.
