
- •2)Риман интегралын есептеу әдістері.Ньютон-Лейбниц формуласы.
- •3)Риман интегралы.Геометриялық және механикалық есептеулерде қолданылуы.
- •4)Көп айнымалы ф-я(каф), оның шегі, үзіліссіздігі.
- •7)Толық дифференциал формасының сақталу қасиеті,(инварианттылығы)
- •8) Ка күрделі ф-ны дифференциалдау,толық туынды формасы
- •10)Кез-келген бағыт б/ша туынды ж/не градиент
- •15) Таңбалары тұрақты сандық қатардың жинақтылығының жеткілікті шарты,Даламбер, салыстыру,т.Б. Қатарларды салыстыру белгілері.
- •18)Функционалдық қатар.Дәрежелік қатардың жинақтылығы, Абель теоремасы.
- •19)Дәрежелік қатардың жинақтылық интервалы ж/не жин r радиусы, негізгі қасиеттері.
- •21)Кейбір элементар функцияның Тейлор қатарына жіктелінуі.
- •22)Екі еселі интеграл, ж/не оның қасиеттері.
- •Сурет 1
- •Полярлық координаталар
- •Сурет 8
- •Сурет 9
- •24)Екі еселі интегралдың кейбір геометриялық және механикалық қолданулары
- •27) Үш еселі интегралда айнымалыны алмастыру, жалпы жағдай
- •28) Үш еселі интегралды цилиндрлік ж/не сфералық коорд жүйесінде есептеу
- •2.6 Үш еселі интегралда сфералық координаталарға көшу
4)Көп айнымалы ф-я(каф), оның шегі, үзіліссіздігі.
Анықтама
1.Егер
белгілі бір ереже немесе заң бойынша М
жиынындағы тәуелсіз
,
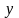 айнымалыларының әрбір қос
айнымалыларының әрбір қос
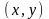 мәніне Z жиынынан алынған z-тің тек қана
бір мәні сәйкес келсе, онда z айнымалысы
М жиынындағы х,
тәуелсіз айнымалыларының функциясы
деп аталады да,
мәніне Z жиынынан алынған z-тің тек қана
бір мәні сәйкес келсе, онда z айнымалысы
М жиынындағы х,
тәуелсіз айнымалыларының функциясы
деп аталады да,
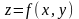 немесе
немесе
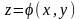 ,
немесе
,
немесе
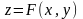 ,
т.с.с белгіленеді.
,
т.с.с белгіленеді.
Нақты
сандар х
пен
-тің
реттелген
қос мәні декарт жазықтығының А
нүктесіне сәйкес келетін болғандықтан,
екі айнымалды функцияларды жазықтықтағы
нүктенің функциясы түрінде жазуға
болады, яғни,
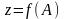 ,
,
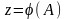 немесе
немесе
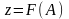 ,
т.с.с.
,
т.с.с.
Жоғарыдағы анықтамада сөз болған М жиыны функцияның анықталу аймағы деп аталады.
Егер
 қос мәні М жиынынан алынса, онда
қос мәні М жиынынан алынса, онда
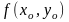 функцияның
функцияның
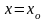 және
және
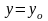 болғандағы дербес мәні болады.
болғандағы дербес мәні болады.
Анықталу
облыстары көрсетіліп, аналитикалық
жолмен немесе формуламен берілген
функциялардың бірнеше мысалдарын
келтірейік. Мына формула
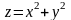 барлық
қос мәндері үшін функцияны анықтайды.
Мына
барлық
қос мәндері үшін функцияны анықтайды.
Мына
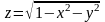 формула тек қана
формула тек қана
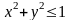 теңсіздігін қанағаттандыратын х
пен
мәндерде функцияны анықтайды, ал мына
теңсіздігін қанағаттандыратын х
пен
мәндерде функцияны анықтайды, ал мына
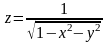 және
және
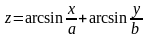 формулалар сәйкесінше
формулалар сәйкесінше
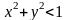 және
және
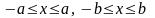 теңсіздіктерін
қанағаттандыратын
қос мәндерінде ғана функцияны анықтайды.
Бұл мысалдардан, екі айнымалды функция
үшін айнымалының өзгеру облысы есептің
шартына қарай әртүрлі және күрделі
болып келетінін көреміз.
теңсіздіктерін
қанағаттандыратын
қос мәндерінде ғана функцияны анықтайды.
Бұл мысалдардан, екі айнымалды функция
үшін айнымалының өзгеру облысы есептің
шартына қарай әртүрлі және күрделі
болып келетінін көреміз.
Осы қарастырылған екі айнымалды функция ұғымын n айнымалды функцияға жалпылауға болады.
Анықтама
2.Егер
белгілі заң немесе ереже бойынша
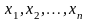 айнымалыларының әрбір реттелген
айнымалыларының әрбір реттелген
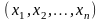 мәндеріне айнымалы
мәндеріне айнымалы
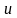 -дың
тек қана бір мәні сәйкестендірілсе,
онда айнымалы
-ды
айнымалы функция деп атайды және былай
белгілейді:
-дың
тек қана бір мәні сәйкестендірілсе,
онда айнымалы
-ды
айнымалы функция деп атайды және былай
белгілейді:
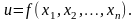
Ал
нақты
сандарынан құралған әрбір реттелген
жүйесіне
өлшемді
кеңістікте бір
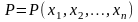 нүктесі
сәйкес келетін болғандықтан,
айнымалды
функцияны
өлшемді
арифметикалық кеңістіктегі нүктенің
функциясы деп жазуға болады, яғни
нүктесі
сәйкес келетін болғандықтан,
айнымалды
функцияны
өлшемді
арифметикалық кеңістіктегі нүктенің
функциясы деп жазуға болады, яғни
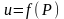 .
.
Егер
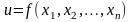 функциясының
айнымалыларының
өлшемді кеңістіктегі М жиынының құрамынан
шықпайтын нақты мәндерінде
функциясының толық анықталған бір мәні
сәйкес келсе, онда М жиыны берілген
функциясының анықталу аймағы деп
аталады.
функциясының
айнымалыларының
өлшемді кеңістіктегі М жиынының құрамынан
шықпайтын нақты мәндерінде
функциясының толық анықталған бір мәні
сәйкес келсе, онда М жиыны берілген
функциясының анықталу аймағы деп
аталады.
Көп айнымалы функцияның шегі.Бізге хОу жазықтығының Q аймағында анықталған функциясы берілсін және осы Q аймағының белгіленген нүктесі болсын.
Анықтама
3.Егер
үшін Q аймағындағы
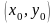 нүктесіне жинақталатын кез келген
нұктелер тізбегі
нүктесіне жинақталатын кез келген
нұктелер тізбегі
 осы
нүктесіне ұмтылғанда оларға сәйкес
осы
нүктесіне ұмтылғанда оларға сәйкес
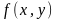 функциясының мәндер тізбегі
функциясының мәндер тізбегі
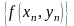 бір ғана А санына ұмтылатын болса, онда
А саны
функциясының
бір ғана А санына ұмтылатын болса, онда
А саны
функциясының
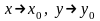 -ге
ұмтылғандағы шегі деп аталады да, былай
белгіленеді
-ге
ұмтылғандағы шегі деп аталады да, былай
белгіленеді
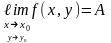 .
(7.4)
.
(7.4)
Анықтама
4.Егер
кез келген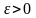 саны бойынша
саны бойынша
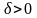 санын
санын
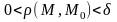 теңсіздігін қанағаттандыратын барлық
М нүктелері үшін
теңсіздігін қанағаттандыратын барлық
М нүктелері үшін
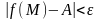 теңсіздігі орындалатындай етіп табуға
болса, онда А саны
теңсіздігі орындалатындай етіп табуға
болса, онда А саны
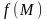 функциясының
функциясының
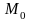 нүктесіндегі шегі
деп аталады және былай жазылады:
нүктесіндегі шегі
деп аталады және былай жазылады:
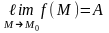 ,
,
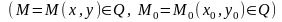
Бұл екі анықтама өзара эквивалентті. Бір айнымалды функциялардың шектері және оларды есептеу ережелерімен әдістері түгелдей көп айнымалды функцияларға да қолданылады.
Көп
айнымалы функциясының үзіліссіздігі.
Айталық,
функциясы Q аймағында анықталған болсын
және
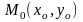 нүктесі Q жиынында жатқан осы жиынның
шектік нүктесі болсын.
нүктесі Q жиынында жатқан осы жиынның
шектік нүктесі болсын.
Анықтама
5.Егер
 функциясының
нүктесі
-ге ұмтылғандағы шегі оның
нүктесіндегі
функциясының
нүктесі
-ге ұмтылғандағы шегі оның
нүктесіндегі
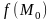 мәніне тең, яғни
мәніне тең, яғни
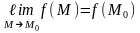 немесе
немесе
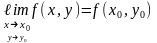
болса,
(мұндағы
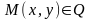 және
және
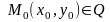 ),
онда
функциясы
нүктесінде
үзіліссіз деп аталады.
),
онда
функциясы
нүктесінде
үзіліссіз деп аталады.
Функция шегінің анықтамасын еске алсақ, функцияның нүктесіндегі үзіліссіздігін мына түрде айтуға болады.
Анықтама
6.Егер
кез келген
санына сәйкес
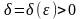 санын,
теңсіздігін қанағаттандыратын барлық
М нүктелері үшін
санын,
теңсіздігін қанағаттандыратын барлық
М нүктелері үшін
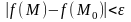 теңсіздігі орындалатындай етіп табуға
болса, онда
теңсіздігі орындалатындай етіп табуға
болса, онда
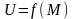 функциясы
нүктесінде үзіліссіз
деп аталады.
функциясы
нүктесінде үзіліссіз
деп аталады.
Мына
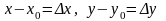 шамалардың әрқайсысы берілген
функциясының
және
айнымалыларының сәйкес өсімшелері, ал
айырым
шамалардың әрқайсысы берілген
функциясының
және
айнымалыларының сәйкес өсімшелері, ал
айырым
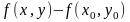 функцияның өсімшесі, яғни
функцияның өсімшесі, яғни
 екенін ескерсек, функцияның нүктедегі
үзіліссіздігінің жоғарыда берілген
анықтамасын былай тұжырымдауға болады:
егер айнымалылардың ақырсыз аз
өсімшелеріне берілген функцияның
ақырсыз аз өсімшесі сәйкес келсе, онда
бұл функция
нүктесінде үзіліссіз болады. Демек,
егер
функциясы
нүктесінде үзіліссіз болуы үшін
екенін ескерсек, функцияның нүктедегі
үзіліссіздігінің жоғарыда берілген
анықтамасын былай тұжырымдауға болады:
егер айнымалылардың ақырсыз аз
өсімшелеріне берілген функцияның
ақырсыз аз өсімшесі сәйкес келсе, онда
бұл функция
нүктесінде үзіліссіз болады. Демек,
егер
функциясы
нүктесінде үзіліссіз болуы үшін
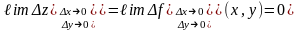 теңдігі орындалуы қажет.
теңдігі орындалуы қажет.
Егер функциясы Q аймағының әрбір нүктесінде үзіліссіз болса, онда ол Q аймағында үзіліссіз функция болады.
хОу жазықтығындағы Q аймағының тұйықталуында үзіліссіз болатын функциясының қасиеттері кесіндіде үзіліссіз болатын бір айнымалды функцияның қасиеттеріне ұқсас.
1) Егер функциясы шенелген тұйық жиында үзіліссіз болса, онда ол осы жиында шенелген функция болады. Демек;
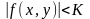 теңсіздігін
қанағаттандыратын
теңсіздігін
қанағаттандыратын
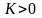 саны табылады.
саны табылады.
2) Егер функциясы шенелген тұйық жиында үзіліссіз болса, онда ол осы жиында өзінің дәл төменгі және жоғарғы мәндерін қабылдайды.
3) Егер функциясы шенелген аймақтың тұйықталуында үзіліссіз болса, онда бұл функция осы жиында бірқалыпты үзіліссіз болады.
5)КАФ-ның дербес туындылары,жоғарғы ретті дербес туындылары, Шварц теоремасы
Бізге
кеңістіктің Q аймағында анықталған
үзіліссіз
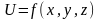 функциясы берілсін. Осы аймақта жататын
функциясы берілсін. Осы аймақта жататын
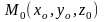 нүктесін аламыз. Егер
нүктесін аламыз. Егер
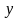 пен
пен
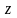 -ке
тұрақты
-ке
тұрақты
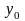 мен
мен
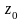 мәндерін беріп
-ті
өзгертетін болсақ, онда
бір айнымалы
-тің
(
мәндерін беріп
-ті
өзгертетін болсақ, онда
бір айнымалы
-тің
(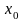 маңайында) функциясы болады. Енді
маңайында) функциясы болады. Енді
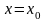 мәніне
мәніне
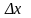 өсімшесін
берсек, онда функцияның
өсімшесін
берсек, онда функцияның
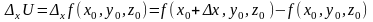
өсімшесін табамыз. Функцияның осы өсімшесі бойынша алынған дербес өсімше деп аталады. Ал мына шек
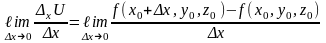
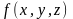 функциясының
функциясының
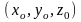 нүктесінде
бойынша алынған дербес
туынды
деп аталады да, келесі символдардың
бірімен белгіленеді:
нүктесінде
бойынша алынған дербес
туынды
деп аталады да, келесі символдардың
бірімен белгіленеді:
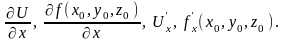
Бұл символдардың төменгі жағында тұрған индекс туындының қай айнымалы бойынша алынатынын көрсетеді. Сондай-ақ, пен тұрақты, ал -ті айнымалы деп алып,
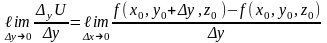
функциясының нүктесіндегі бойынша алынған дербес туындысын анықтаймыз.
Берілген функциясының бойынша алынған нүктесіндегі дербес туындысы да осылай анықталады.
Дербес туындыны есептеуде бір айнымалды функциясының туындысын табу ережелері түгелдей қолданылады.
Мысалы:
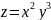 .
Ш:
.
Ш:
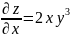 ,
,
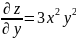 .
.
Жоғарғы ретті дербес туынды
Егер
функциясының Q аймағында айнымалылардың
бірі бойынша дербес туындысы бар болса,
онда бұл туындыны
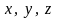 айнымалыларының функциясы деп қарастырып
және осы аймақтың
нүктесінде оның
айнымалылары бойынша дербес туындылары
бар деп есептеп, одан екінші ретті дербес
туынды алуға болады.
айнымалыларының функциясы деп қарастырып
және осы аймақтың
нүктесінде оның
айнымалылары бойынша дербес туындылары
бар деп есептеп, одан екінші ретті дербес
туынды алуға болады.
Егер бірінші туынды бойынша алынса, онда оның бойынша алынған екінші ретті туындыларын былай белгілейді:
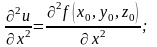
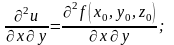
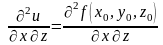
немесе
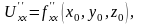
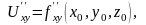
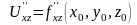
Келесі 3-ші, 4-ші тағы сол сияқты ретті туындылар да осылай анықталады. Әр түрлі айнымалылар бойынша алынған жоғары ретті туындыны аралас дербес туынды дейді.
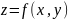 үзіліссіз
болса дербес туындылары бар.
үзіліссіз
болса дербес туындылары бар.
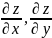 – 1 ретті
туындылар,
– 1 ретті
туындылар,
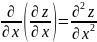 – x бойынша 2 ретті туынды
– x бойынша 2 ретті туынды
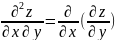 - аралас
2 ретті туынды,
- аралас
2 ретті туынды,
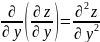 y бойынша 2 ретті туынды
y бойынша 2 ретті туынды
екінші
ретті туынды мына формуламен анықталады:
![]() .
.
![]()
![]()
![]()
![]()
Шварц
теормасы.
Егер z=xy функциясы және оның 1-ретті
дербес туындылары үзіліссіз (М нүктесінде)
болса, онда
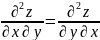
6) КАФ-ның дифференциалдануы толық дифференциал,және оны жуықтап есептеу
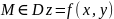
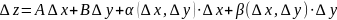 (1)
(1)
Егер ф-ның өсімшесін 1-ші түрде жазылатын болса => z функциясын М нүктесінде дифференциалданады д.а. Мұндағы α,β – шексіз аз шамалар, егер ∆х →0, ∆y→0, A,B – ақырлы сандар.1-түрдегі формуланы алғашқы 2 мүшесінің қосындысы басты бөлігін құрайды. ∆х ,∆y мүшесін сызықты ең ба
сты
бөлігін дифференциалы д.а.
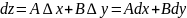
Теорема-1(қажетті
ж/не жеткілікті шарты) Егер
функциясы М нүктесінде дифференциалданатын
болса, онда ол сол нүктеде үзіліссіз
болады,
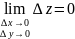 ,
,
Жеткілікті
шарты. Егер
M0(x0,y0)
нүктесінде үзіліссіз болады, ж/не оның
дербес туындылары сол маңайда үзіліссіз
б/са, онда бұл ф/я сол нүктеде
дифференциалданады ж/не
 дербес туындалары болады.
дербес туындалары болады.
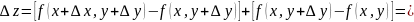 , Лагранж
теоремасы б/ша
, Лагранж
теоремасы б/ша
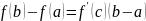
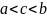
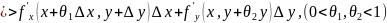
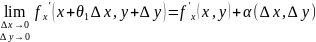
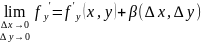
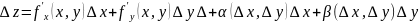
Анықтама.
өсімшесінің
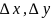 -ке
қарағанда ең басты бөлігің функцияның
толық дифференциалы д.а.
-ке
қарағанда ең басты бөлігің функцияның
толық дифференциалы д.а.
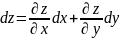
2-ретті толық туынды
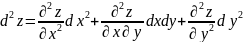
Мысал
1:
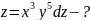
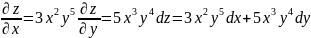
Мысал
2. Берілген
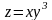 функцияның толық дифференциалын табу
керек.
функцияның толық дифференциалын табу
керек.
Шешуі.Бұл
функцияның дербес туындыларын табайық.
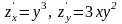 демек,
демек,
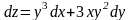 .
.
