27) Үш еселі интегралда айнымалыны алмастыру, жалпы жағдай

 Үш еселі интегралда айнымалыны ауыстыру

 Егер функциясы V тұйық облысында үзіліссіз болса, ал

(1)

функцияларының UVW кеңістігіндегі Т тұйық облысында үзіліссіз дербес туындылары бар болып және осы облысты XYZ кеңістігіндегі V облысына бірмәнді бейнелесе, онда келесі теңдік орындалады:

(2)

мұндағы - якобиан бейнелеуі

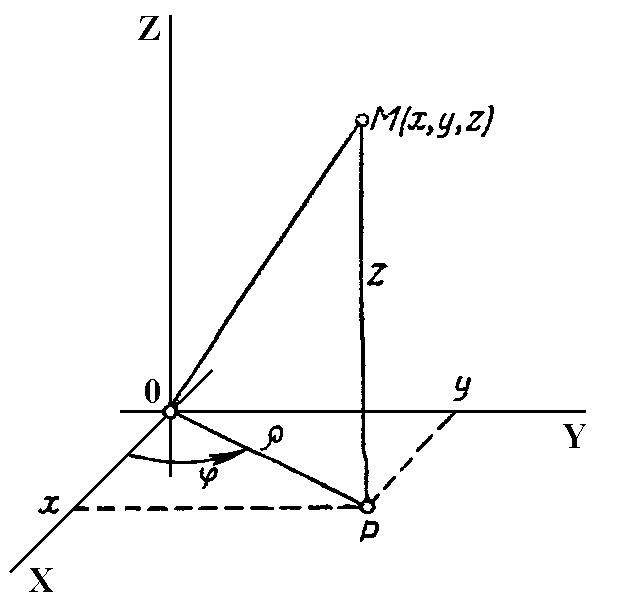
сурет 4.16.1

28) Үш еселі интегралды цилиндрлік ж/не сфералық коорд жүйесінде есептеу

XYZ кеңістігіндегі нүктесінің орны үш санды белгілеуден бірмәнді анықталады, мұндағы - М нүктесінің XOY жазықтығындағы проекциясы радиус-вектордың ұзындығы, - OX өсімен радиус-вектор арасындағы бұрыш, z – М нүктесінің аппликатасы. Олар М нүктесінің декарттық координаталарымен келесі қатынастар арқылы байланысады:

(1)

Анықтама бойынша , .

Якобиан бейнелеуі:

берілген жолақта теріс емес ( жолақтың шекарасында ғана).

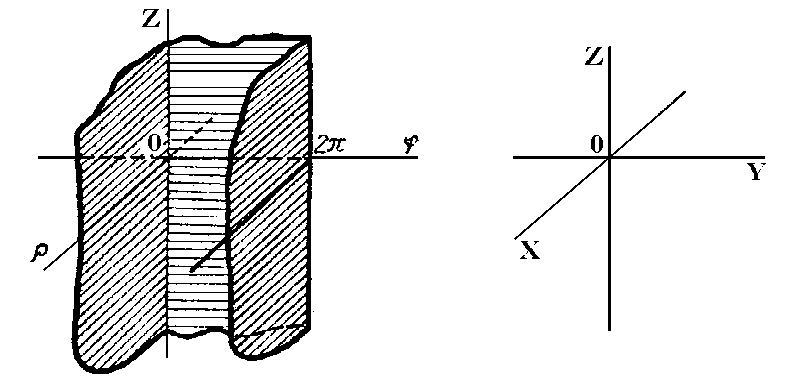
сурет 4.16.2

(1) формуласын үш еселі интегралға қолдану үш еселі интегралда декарттық координатадан цилиндрлік координатаға көшу формуласы деп аталады:

Мұнда Т – (1) формуласы арқылы V облысынының кеңістігіндегі бейнеленген облысы.

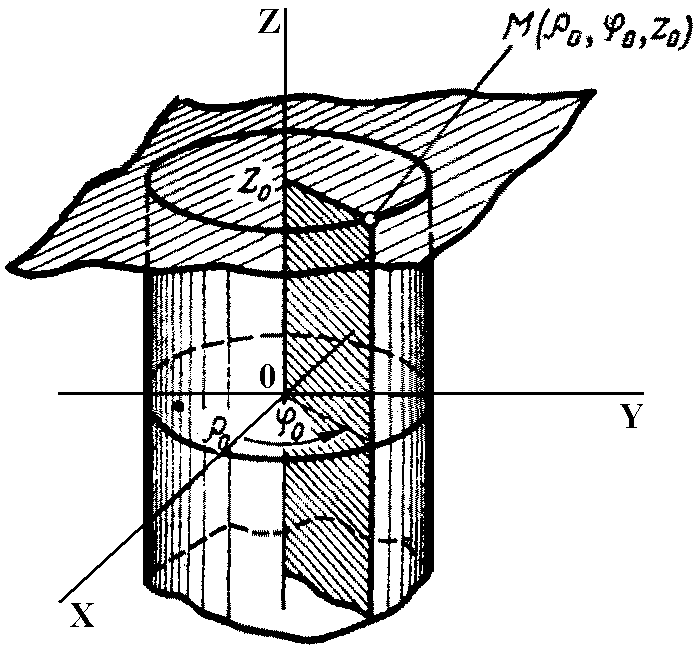
Мысалы. беттерімен шектелген дененің V көлемін цилиндрлік координата арқылы есептеңіз.

Т арқылы беттерімен шектелген кеңістігінің облысын белгілейміз (сурет 4.16.4.).

сурет 4.16.3

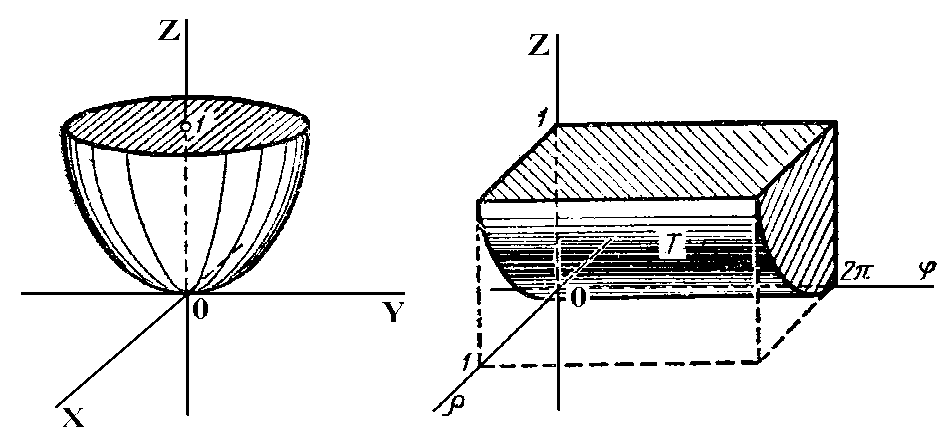
сурет 4.16.4

2.6 Үш еселі интегралда сфералық координаталарға көшу

 XYZ кеңістігіндегі нүктесінің сфералық координаталары деп сандарын айтамыз, мұндағы - радиус-векторының ұзындығы, - радиус-вектордың XOY жазықтығындағы проекциясымен OX өсінің арасындағы бұрыш, ал - М нүктесімен радиус-вектор арасындағы бұрыш (сурет 4.16.6.). М нүктесінің бұл сандармен берілуі оның XYZ кеңістігіндегі орнын анықтайды.

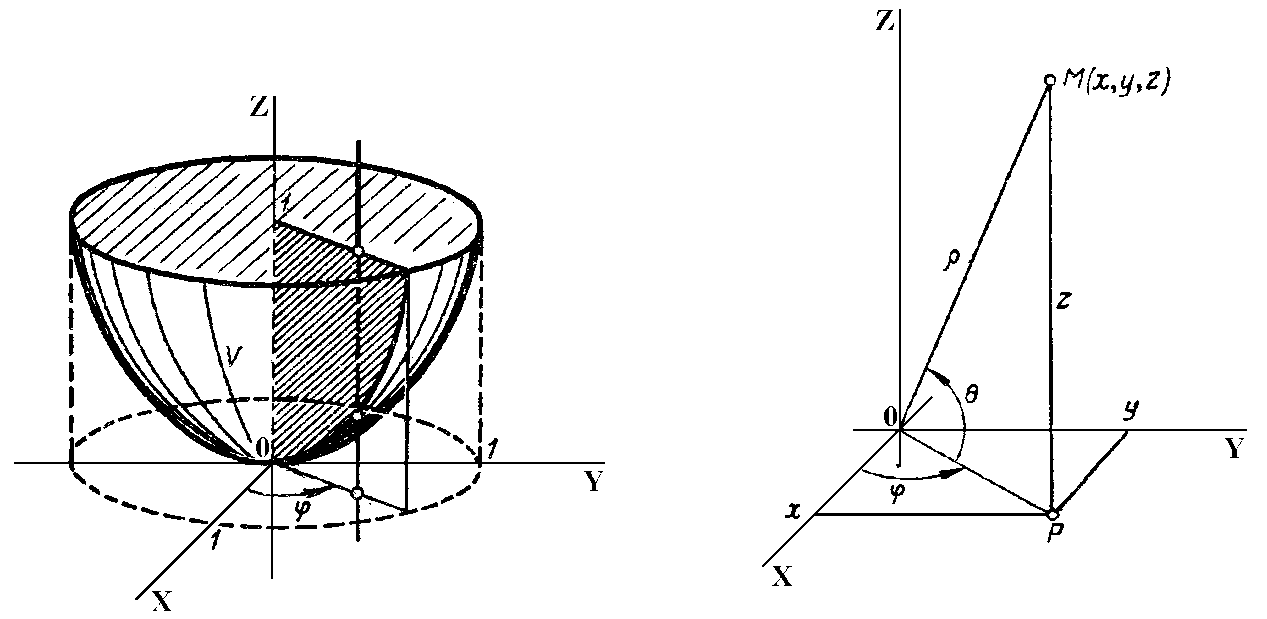
сурет 4.16.5 сурет 4.16.6

М нүктесінің x, y, z декарттық координаталары сфералық координаталармен келесі формула арқылы байланысады:

. (1)

Анықтама бойынша ,

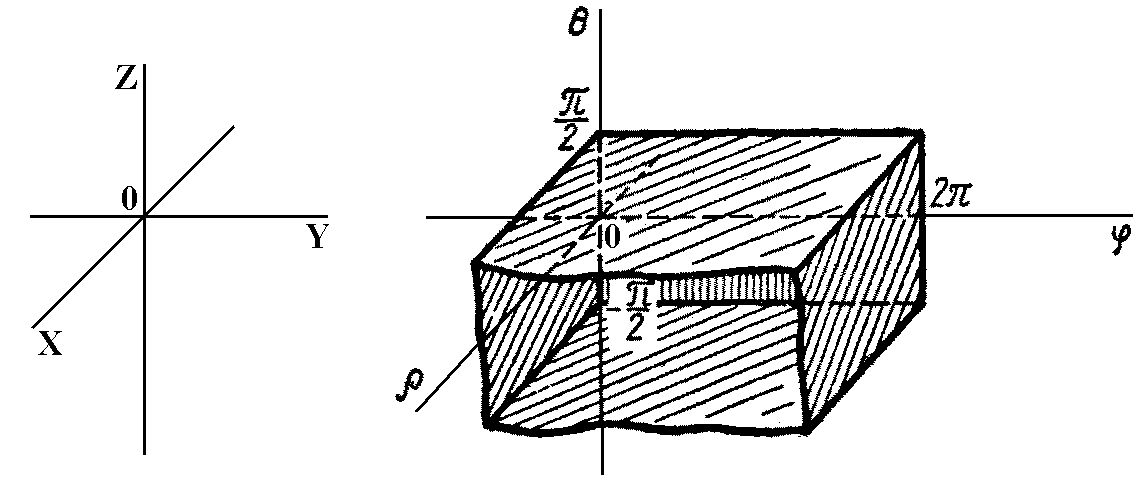
сурет 4.16.7

кеңістігіндегі жазықтығына XYZ кеңістігінде сфера сәйкес келеді, ал жазықтығына - OZ өсінен OX-пен бұрыш жасап өтетін жарты жазықтық, ал жазықтығына - жасаушылары XOY жазықтығымен бұрыш жасайтын, О төбесі болатын дөңгелек конус сәйкес келеді (сурет 4.16.8.). Якобиан бейнелеуі:

Берілген жолақта якобиан бейнелеуі теріс емес, тек жолақ шекарасында нөлге айналады.

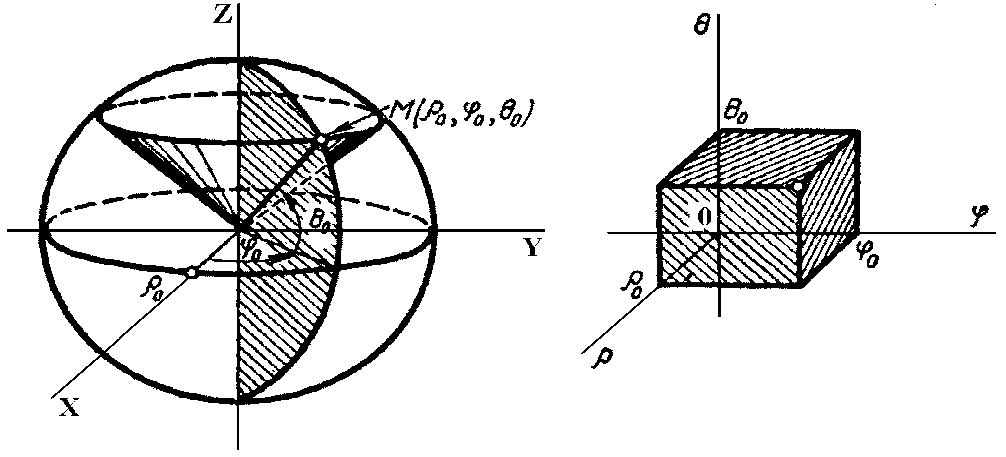
Сурет 4.16.8

(1) бейнелеуі арқылы үш еселі интегралда айнымалыны ауыстыруға болады:

(2)

мұнда Т – V облысының кеңістігіндегі бейнесі. Бұл формула үш еселі интегралда декарттық координатадан сфералық координатаға көшу деп аталады.

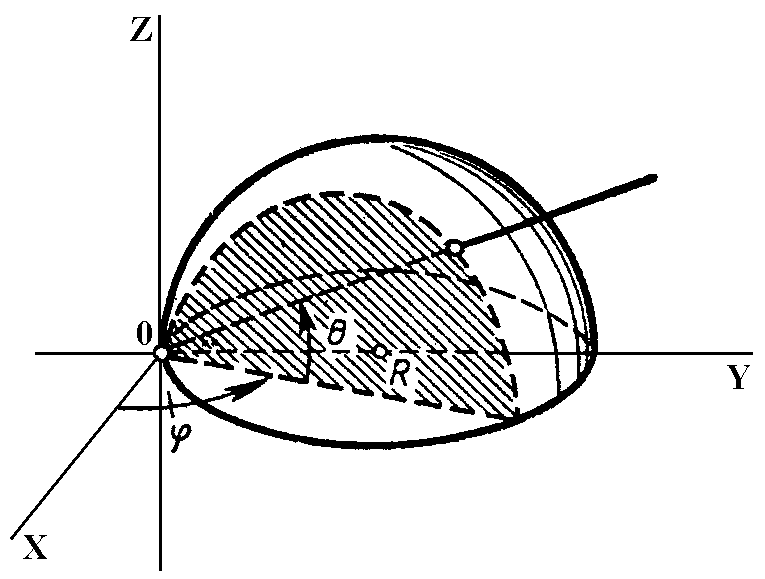
Үш еселі интегралды геом ж/не механикалық есептерде қолдану

 Егер XYZ кеңістігінде V облысының масса тығыздығы белгілі болса, онда V облысына байланысты статикалық моменттер келесі формулалармен есептеледі:

Координат өстеріне қатысты инерция моменттері:

Ауырлық центрінің координаттары:

32)Функциялық қатар.Функциялық қатардың жинақты болу облысы.

Енді мүшелері функциялар болатын қатарларды қарастырайық. Ол функциялар айналымы х-тің өзгеру облысында анықталған. Мысалы, қатары функциялық қатар. Өйткені, оның мүшелерінің әрқайсысы функциялар болады. _(5.1) түріндегі қатарды функциялық қатар д.а.. функциясының анықталу облысында жататын мәніне (5.2) түріндегі сандық қатар сәйкес келеді. Бұл қатар жинақты, не жинақсыз болуы мүмкін. Егер ол жинақты болса, онда нүктесін (5,1) қатарының жинақтылық нүктесі дейді. Егер (5.2) қатары нүктеде жинақсыз болса, онда ол нүктені функциялық қатардың жинақсыздық нүктесі д.а.. функциясынан алынған нүктелердің кейбірінде қатар жинақты, ал басқаларында жинақсыз болуы мүмкін.

АНЫҚТАМА. Функциялық қатардың жинақты болатын нүктелер жиыны, оның жинақтылық облысы д.а.. Функциялық қатардың дербес қосындысы, яғни алғашқы мүшелерінің қосындысы (5.3) айнымалы х-тің функциясы болады. Функциялық қатардың жинақтылық облысының анықтамасынан бұл облыстың кез келген нүктесінде дербес қосындысының -дағы шегі бар болатыны көрінеді. Жинақтылық облысна тиісті емес нүктелерде дербес қосындысының шектері болмайды. Сонымен, функциялық қатар қосындысы-жинақтылық облысында анықталған айнымалы х-тің функциясы болады екен. Бұл жағдайда, деп жазады. Егер функциялық қатар жинақты және оның қосындысы болса, онда айырымын берілген қатардың қалдығы немесе қосымша мүшесі д.а.. Оны деп белгілейді. Сонда Бұл жерде, Қатардың қалдығы функциялық қатардың алғашқы мүшелерін шығарып тастағаннан алынатын қатардың қосындысы болады: (5.4)

Дұрыс жинақты функциялық қатарлар және олардың қасиеттері.АНЫҚТАМА. Егер (5.1) функциялық қатары мүшелерінің абсолют шамалары кесіндісінде оңтаңбалы жинақты (5.6) сандық қатарының сәйкес мүшелерінен артық болмаса, яғни n=1,2,3,… (5.7) болса, онда (5.1) қатарды дұрыс жинақты қатар дейді. Енді кейбір қасиеттерін дәлелдеусіз келтірейік. I-теорема. кесіндісінде дұрыс жинақты болатын функциялық қатар бұл кесіндінің кез келген нүктесінде абсолютті жинақты болады. Саны шекті үздіксіз функциялар қосындысы да үздіксіз функция болатыны белгілі. Осындай қасиетке дұрыс жинақты болатын мушелері үздіксіз функциялық қатарда ие болады.

2- теорема. Егер дұрыс жинақты қатарының мүшелері кесіндісінде үздіксіз болса, оның қосындысы бұл кесіндіде үздіксіз болады. Егер болса, онда

Ал, қосылғыштар саны шектеусіз артқанда, бұл қасиет орындалмайды, яғни қатарлар үшін қолдана алмаймыз. Дегенмен, бұл қасиет кесінді де дұрыс жинақты функциялық қатар үшін орындалады.

3-теорема. Егер кесіндіде дұрыс жинақты функциялық қатарының мүшелері бұл кесіндіде үздіксіз болса, оны мүшелеп интегралдауға болады. Бұл айтылғаннан егер және нүктелері кесіндіде жатса, онда (5.8)

теңдігі орындалатыны шығады.

4-теорема. Айталық функциялық қатары кесіндісінде жинақты және оның мүшелерінің ( n=1,2,3,…) туындылары үздіксіз болсын. Сонда, егер қатарды мүшелеп дифференциалдаудан алынған қатар -да дұрыс жинақты болса, онда оның қосындысы берілген қатардың қосындысының туындысына тең, яғни

болады.

5-теорема. Егер кесіндіде дұрыс жинақты қатарды шектелген функциясына көбейткеннен алынатын (5.10) қатары да бұл кесіндіде дұрыс жинақты болады.

72