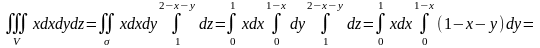24)Екі еселі интегралдың кейбір геометриялық және механикалық қолданулары

Екі еселі интегралды жоғарыда айтылғандай жазық фигураның ауданын, дененің көлемін есептеуге қолдануға болады. Бірнеше мысалдар қарастырайық.

Мысал 1. 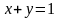сызықтарымен шектелген облысының ауданын тап.

облысы сол жағынан 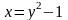парабола доғасымен және оң жағынан 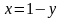түзуімен шектелген параболалық сегмент болып табылады. Параболаның теңдеуі мен түзу теңдеуін бірге шеше отырып, олардың қиылысу нүктелерінің ординатасын табамыз: y=-2, y=1.

Осыдан,

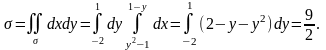
Ескерту. Егер біз интегралдау ретін керісінше алатын болсақ облысын алдын-ала екі облысқа бөлу керек болады.

Мысал 2. y=x², y=1, z=0, z=x²+y² беттерімен шектелген V дененің көлемін тап.

Берілген дене табаны болатын, жоғарыдан z=x²+y² параболоидпен шектелген цилиндрлік дене болғандықтан:

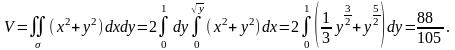
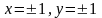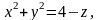
Мысал 3. Жақтары және 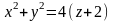параболоидтармен шектелген призмалық дененің көлемін тап.

Дененің V көлемін ХОҮ жазықтығының сәйкес жоғарғы және төменгі жақтарында жатқан екі дененің көлемдерінің V₁ және V₂ қосындысы түрінде қарастырамыз. Яғни

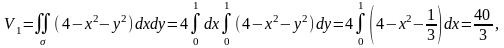
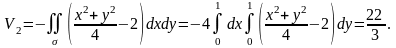
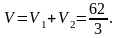
S бетінің ауданын табу формуласы:

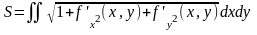
Екі еселі интегралдың геометриялық мағынасы

Цилиндрлік дененің көлемін табу есебіне оралайық. Қарастырып отырған функциясы тұйық облысында үзіліссіз болса, онда нүктелері тұйық облыстарында қандай болса да

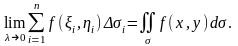
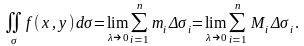
функциясы облыстарында (m_i) ең кіші немесе (M_i) ең үлкен мәндерін қабылдайтындай етіп, нүктелерін таңдай отырып, келесі теңдікті аламы: 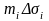және қосылғыштары табаны болатын цилцндр көлеміне тең. 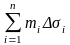және 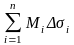қосындылары сәйкесінше іштей және сырттай сызылған V цилиндрлік денелердің көлемдеріне тең. 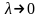бұл көлемдер ортақ шекке ие болады, берілген дене кубталады және оның V көлемі екі еселі интегралға тең: 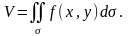Осыдан екі еселі интегралдың геометриялық мағынасы: тұйық облысында теріс емес, үзіліссіз функциясының екі еселі интегралы жоғарыдан бетпен шектелген, XOY жазықтығындағы табаны болатын цилиндрлік дененің көлеміне тең. Егер облысында 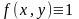болса, онда цилиндрлік дене табаны ал биіктігі 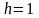болатын цилиндрді білдіреді. Оның көлемі сан жағынан табанының ауданына тең. Осылайша, екі еселі интеграл арқылы облысының ауданын бұрыннан белгілі формуламен есептейміз 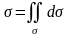немесе .

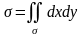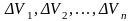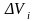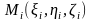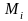25)Үш еселі интеграл ж/не оның қасиеттері XYZ кеңістігінде V кубталатын тұйық облысында кез келген функция берілсін. V облысын ортақ ішкі нүктелері болмайтын n облыстарға бөлейік. облыстарынының әрбірінен нүктелерін аламыз. функциясының нүктелеріндегі мәндерін көлемдеріне көбейтіп, осындай көбейткіштерді қосамыз. Алынған 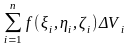қосынды функциясы үшін V облысы бойынша интегралдық қосынды деп аталады. функциясы үшін V облысы бойынша шексіз интегралдық қосынды құруға болады.

Егер V облысында бөлу қадамы нөлге ұмтылғанда интегралдық қосындының шегі бар болса, онда бұл шек функциясының V облысы бойынша үш еселі интеграл деп аталады және оны

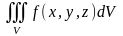немесе

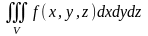
символымен белгілейді.

Мұндағы - интеграл астындағы функция, V – интегралдау облысы, x, y және z – интегралдау айнымалылары, 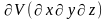- көлем элементі.

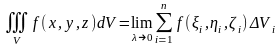
Үш еселі интегралдар екі еселі интегралдардың үш өлшемді кеңістіктегі жалпы жағдайы.

Теорема 1. Егер функциясы V тұйық облысында үзіліссіз болса, онда үш еселі интеграл бар болады.

Үш еселі интегралдың геометриялық мағынасы: V дененің көлемін үш еселі интеграл арқылы есептеуге болады

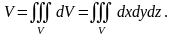
Үш еселі интегралдың механикалық мағынасы: V дененің массасы

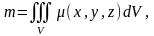
формуласымен анықталады, мұндағы 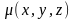- масса тығыздығы.

Үш еселі интегралдың негізгі қасиеттері:

1. Үш еселі интеграл интегралдау айнымалыларын белгілеуден тәуелді емес, яғни

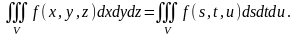
2. Тұрақты көбейткішті үш еселі интеграл таңбасының алдына шығаруға болады:

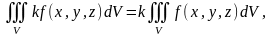
мұндағы k – сан.

3. Екі функция қосындысының үш еселі интегралы осы функциялардың үш еселі интегралдарының қосындысына тең:

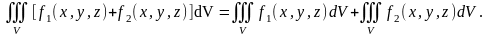
4. Егер V облысы екі V1 және V2 облыстарына бөлінсе, онда

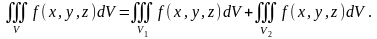
5. Егер V облысында

6. Егер V облысында

онда

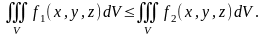
7.

27) Үш еселі интегралды қайталама интеграл арқылы есептеу Теорема 1. V облысы төменнен және жоғарыдан 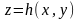және 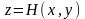беттерімен шектелген болсын, мұндағы 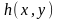және 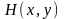- XOY жазықтығындағы тұйық облысында үзіліссіз функциялар. Онда V тұйық облысындағы кез келген үзіліссіз функциясы үшін келесі формула орындалады

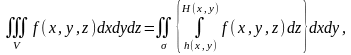(1)

Бұл формула үш еселі интегралды анықталған интегралдың екі еселі интегралына әкеледі.

Теңдіктің оң жағындағы интеграл келесі түрде жазылады:

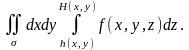
Үш еселі интегралды (1) формуласы бойынша есептегенде алдымен z айнымалысы бойынша (x және y- тұрақтылар) ішкі интеграл есептеледі, одан кейін x және y бойынша облысында екі еселі интеграл есептеледі.

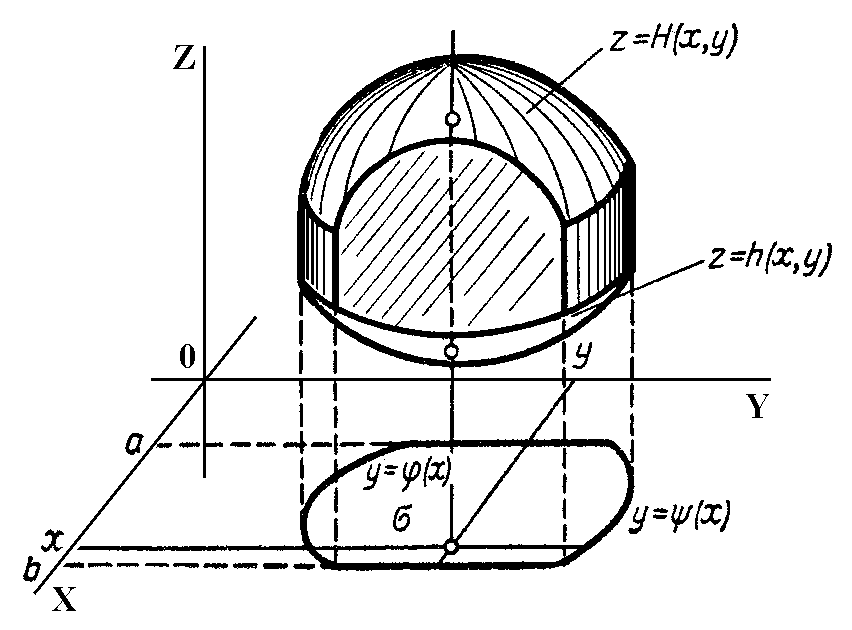
сурет 4.13.1

Егер облысы XOY жазықтығында x=a, y=b (a<b), 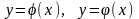сызықтарымен шектелсе, [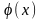 және [а, b] кесіндісінде үзіліссіз функциялар , сонымен қатар (сурет 4.13.1.)], онда екі еселі интгералдан облысы бойынша қайталанбалы интегралға көшіп

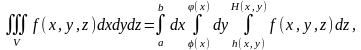(2)

формуласын аламыз.

Егер V облысы - x=a, x=b (a<b), y=c, y=d (c<d), z=l, z=k (l<k) жазықтықтарымен шектелген параллелепипед болса, онда (2) формуласы:

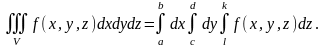
Егер функциясы әрқайсысы бір ғана айнымалыдан тәуелді үш функцияның көбейтіндісі болса,

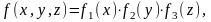
онда V параллелепипеді бойынша үш еселі интеграл осы функциялардың анықталған интегралдарының көбейтіндісіне тең.

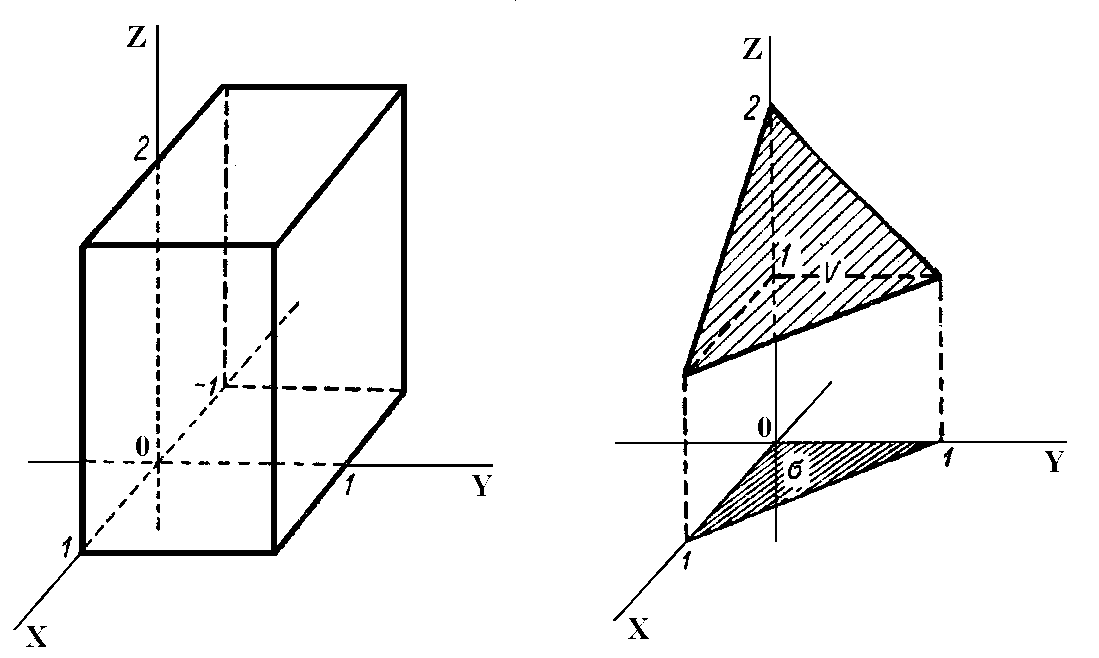
сурет 4.13.2 сурет 4.13.3

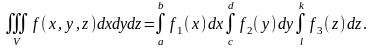
Мысал 1. x = -1, x = +1, y = 0, y = 1, z = 0, z = 2 жазықтықтарымен шектелген параллелепипед бойынша 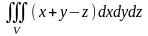үш еселі интегралын есептеңіз. (2) формуласы бойынша:

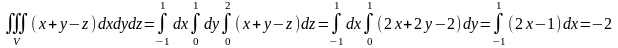
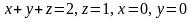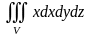Мысал 2. жазықтықтармен шектелген V облысы бойынша үш еселі интегралды есептеңіз(сурет 4.13.3.).

V облысы XOY жазықтығына 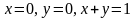түзулерімен шектелген үшбұрышы болып проекцияланады. 1 және 2 формулаларын қолданамыз: