Т.К. Обычно , то без существенных погрешностей можно принять и .
Используя эти упрощения, уравнение (17) примет вид:
(18)
Вводя
коэффициент
,
уравнение (18) удобно представить в виде
(19)
при увеличении z k быстро стремится к 1.
Математическая модель работы насоса однократного действия.
Рассмотрим
камеру насоса в некоторый момент времени
t,
соответствующий углу поворота
.
Введём контрольный объём ADCE.
За время dt
камера
повернётся на угол
и её контрольный объём увеличится на
и уменьшится на
.
За
счёт всасывания контрольного объёма
камера уменьшается на величину
и увеличивается на величину объёма
нагнетания
.
Кроме того, необходимо учесть увеличение
контрольного объёма за счёт утечек
.
Тогда изменение контрольного объёма
будет равно:
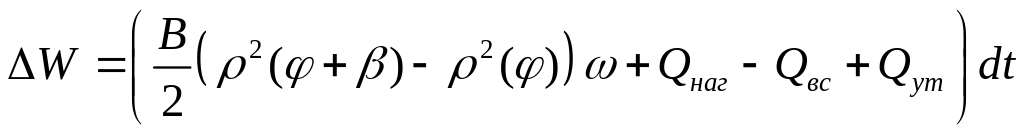
Скорость изменения объёма камеры насоса:
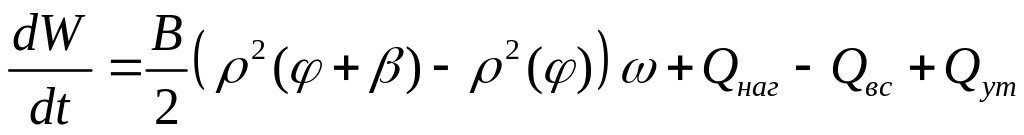(20)
Используя уравнение сжимаемости:
(21)
Уравнение (20) приводится к виду
(22)
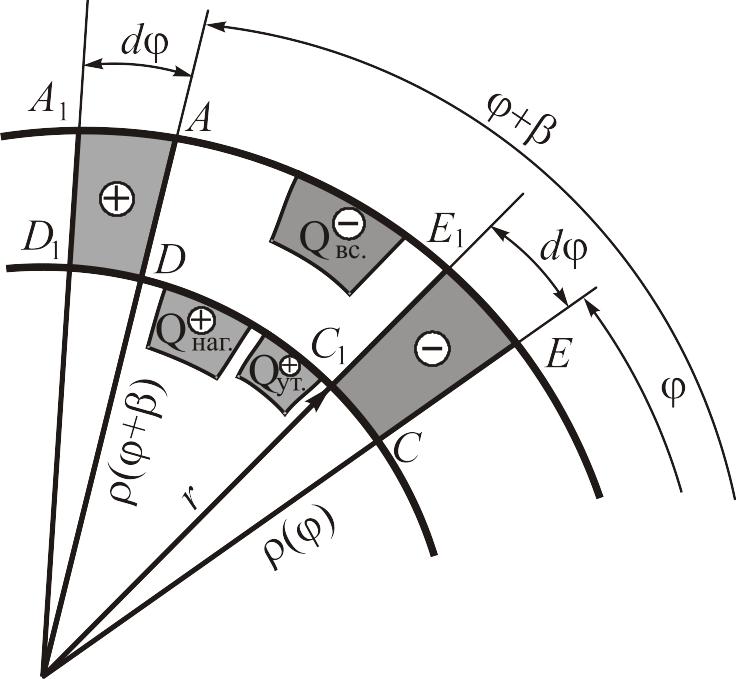
Рис. 4. Изменение контрольного объёма камеры насоса.
Учитывая,
что
,
а
,
уравнение (22) окончательно примет вид:
(23)
Обозначая
площадь контакта зоны всасывания с
камерой насоса через
и зоны нагнетания
,
а давление в этих зонах
и
(эти давления принимают постоянными
величинами), соответствующие расходы
их обмена жидкостью с камерой насоса
можно описать формулами:
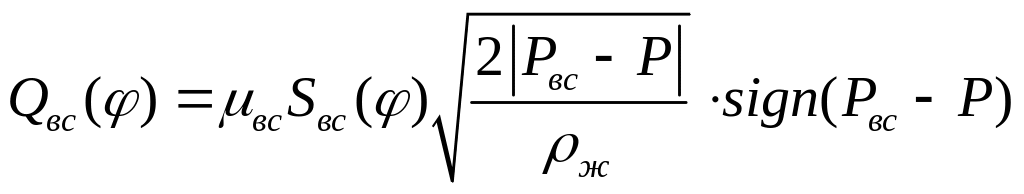(24а)
(24б)
Здесь
и
– соответствующие коэффициенты расхода.
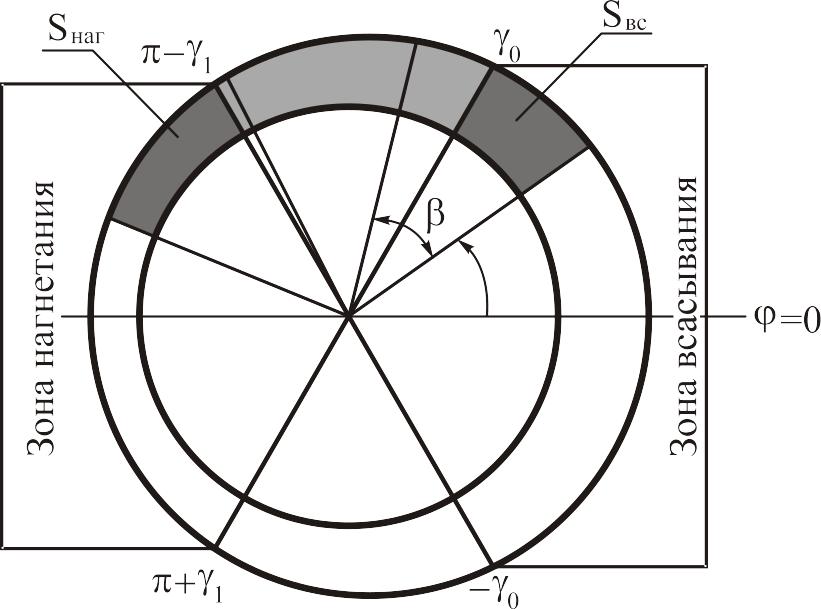
Анализ существующих конструкций зон всасывания и нагнетания показывает их чрезвычайное многообразие.
Поэтому
на данной стадии исследования будем
полагать, что зона всасывания находится
в диапазоне углов
и площадь её контакта с камерой
определяется следующим образом:
(25)
Будем
также полагать, что зона нагнетания
находится в диапазоне углов
и определяется следующим образом:
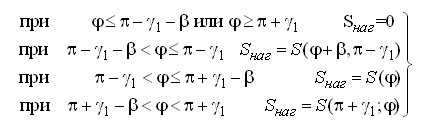(26)
Для
эффективной работы пластинчатого насоса
необходимо выполнения условия
.
Только при выполнении этого условия
камера насоса не будет одновременно
контактировать с зонами всасывания и
нагнетания.
Определение и
В
диапазоне углов
и
давление в камере насоса, рассчитываемое
по формуле (22) может упасть ниже
,
что нефизично. Поэтому уравнение (23)
следует дополнить условием:
если
(27)
Проведём оценку максимальных давлений, которые могут возникнуть в камере насоса.
Теоретически, при отсутствии подвода, отвода и утечек максимальное давление можно определить по формуле:
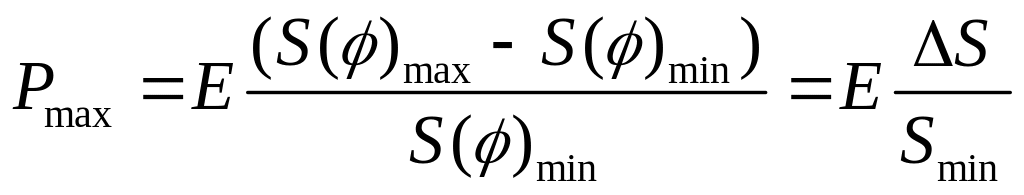
Для параметров базового насоса с использованием формул (14) и (15), получаем:
Если учитывать подвод и отвод насоса, то максимальное давление насоса зависит от угла уплотнительной перемычки .
Расчёты
показывают, что при
,
а при
.
В
действительности давление
в камерах насоса на порядок меньше. Это
объясняется тем, что наличие утечек,
несмотря на их малую величину, вследствии
малой сжимаемости рабочей жидкости,
резко снижает
.
Опытные данные показывают, что в пластинчатом насосе насчитывается 6 различных типов утечек между элементами. Основной из них составляющей не менее 70% всех утечек составляют утечки через зазоры между торцами распределительных дисков и кромками пластин. Поэтому расход утечек рассчитывался по формуле:
(28)
здесь
–
величина зазора;
–
высота камеры, определяется по формуле
(11б);
–
коэффициент расхода, принимаемый при
расчётах равный 1;
– давление
в зазоре.
Так
как в большинстве насосов под пластины
подводят давление в зоне всасывания
,
а в зоне нагнетания
,
то было принято
рассчитывать по формуле:
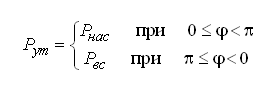(29)
Зазоры в реальных насосах между кромками пластин и торцами распределительных дисков находятся в диапазоне от 0,01 мм до 0,07 мм.
На основе полученной математической модели была создана программа расчета влияния конструктивных и режимных параметров на работу насоса.