Пптрн11ия п»,нмм дяш-.Рппм тяр'чм няппимрп мп'-к-рт fil,iTt, nRhwpuhp •aniaL't-nrii-il ппч

	n=2
	11=1	2
		E,
	n=0	Eo
		—————————»
		2
	f———>
	L

переходе его из металла в вакуум: на границе он встречает потенциальный барьер, преодоление которого связано с совершением работы выхода.

Схема потенциального барьера, имеющего ширину «d» и высоту «и» изображено на рисунке.

По классическим представлениям поведение частицы имеет следующий характер. Если энергия частицы больше высоты барьера Е>и

То частица беспрепятственно проходит над барьером. Если же Е>и, то частица отражается от барьера и летит в обратную сторону.

Совершенно иначе выглядит поведение частицы согласно квантовой механики.

Во-первых, даже при Е>и имеется отличная от нуля вероятность того, что частица отразится от барьера и полетит в обратную сторону.

Во-вторых, при Е>и имеется отличная от нуля вероятность того, что частица проникнет сквозь барьер и окажется в области, где X>d. Такое, совершенно невозможное с классической точки зрения поведение микрочастицы вытекает непосредственно из уравнения Шредингера.

Расчет показывает, что вероятность просачивания частицы через барьер может быть выражена формулой:

-*^<l4lm(u-E)

D=e * где d-ширина, U-высота барьера, Е-полная энергия частицы. Как видно из этой формулы, чем больше ширина и высота барьера, а также чем больше масса микрочастицы, тем меньше вероятность прохождения её через барьер. Это явление носит название ту line. i ыюго эффекта.

С классической точки зрения туннельный эффект представляется абсурдным, т.к. находящейся в туннеле частица имеет Е>и и следовательно должна иметь отрицательную кинетическую энергию. В квантовой механике деление полной энергии на кинетическую и потенциальную не имеет смысла и противоречит принципу неопределённости. Это видно из того, что если бы частица обладала определённой кинетической энергией, то она имела бы определённый импульс Р. Аналогично, если частица имеет определённую потенциальную энергию, то значит, она находится в точном заданном месте пространства. Поскольку координата и импульс не могут одновременно иметь определённых значений, то не могут быть точно определены кинетическая и потенциальная энергия частицы. Таким образом, хотя полная энергия частицы имеет вполне определённое значение, она не может, представлена в виде суммы точно определённых значений кинетической и потенциальной энергии. Следовательно, говорит о том, что частица, находящаяся в туннеле обладает отрицательной кинетической энергией, с точки зрения квантовой механики не имеет смысла.

Атом водорода квантово-механической теории.

Атом водорода представляет собой систему, состоящую из одного электрона и одного протона, между которыми действует электростатическое притяжение. Потенциальная энергия электрона в поле ядра в соответствии с законом Кулона

и =--

4w„r

где Г - расстояние от электрона до протона. Уравнение Шредингера для этого случая имеет вид:

АУ+^^+^^О И~ 4лг'„/'

Решение его представляет довольно сплошную задачу, поэтому ограничимся только

описанием результатов:

1. Точное решение этого уравнения приводит к появлению дискретных энергетических уровней, обладающих теми же значениями энергии атома водорода, какие получались в теории Бора. Однако в теории Бора этот результат был получен путём внесения постулатов, в квантовомеханической теории он получается как следствие самой теории.

2. Точное решение уравнения Шредингера позволяет найти не только все энергетические уровни атома водорода, но и все волновые функции. Это решение показывает, что в основном состоянии электрон характеризуется одной волновой функцией Т,. В возбужденных состояниях электрона таких функций несколько.

Квантовому числу П=2 соответствует четыре волновых функций, квантовому числу п=3 - девять значений и т.д., т.е. в общем случае состоянию с квантовым числом П>1 соответствует П значение волновой функции. Таким образом, состоянию электрона с одним значением энергии соответствует несколько значений волновой функции. Эти значения отличаются между собой величиной вращательного момента импульса и значением его проекции на какое-либо произвольное направление. Состояние с одинаковой энергией называются вырожденными, а число различных состояний с каким- либо значением называется кратностью вырождения соответствующего энергетического уровня. Кратность вырождения уровней водорода равна П².

3. Решение уравнения Шредингера для атома водорода показывает также, что вращательный момент импульса электрона имеет ряд дискретных значений, определяемых по формуле

L=V/.(/+1)-^

где /- коэффициент, называемый орСтпииьным квинтовым числом. Он

характеризует эксцентриситет орбиты электрона. Величина / может принимать любые целые значения от О до П - 1, где n - главное квантовое число.

4. Решение уравнения Шредингера показывает, что проекция вращательного момента импульса на заданное направление равна

/ ^h L. =т—

2л где т- коэффициент, называемый магнитным квантовым числом.

Он определяет пространственную ориентацию орбиты электрона. Величина ГП может принимать любые целые значения от -/ до +/ .включая ноль. Итак, состояние электрона в атоме характеризуется тремя квантовыми числами n, m, /.

В атомной физике применяются заимствованные из спектроскопии условные обозначения состояний электрона с различными значениями момента импульса. Численные значения квантового числа / обозначают обычно буквами по следующей схеме:

/:0, 1,2,3,4,5. Буква: s, р, d,f, g, h.

Электрон, находящийся в состоянии с /= О, называют S-электроном, с /=1- р-электроном, и т.д.

Электронные состояния принято записывать так: главное квантовое число п-цифрой, а число 1- соответствующей буквой. Например, электрон в состоянии с п=3 и / = Г обозначается символом ЗР и т.д. Поскольку 1 - всегда меньше п возможны следующие состояния электрона:

IS

2S.2P

3S,ЗР, 3d

4S,4P,4d,4f и т.д.

Энергетические переходы у атома водорода определяются только значениями главного квантового числа «П». Чтобы числа «/» и «т» стали играть роль, нужно снять «вырождение». Для атома водорода это можно сделать, помещая его в магнитное поле. Решая уравнение Шредингера, мы получаем данные о вероятности нахождения электрона в том или ином месте. При этом получается, что заряд электрона размазан с различной плотностью по всему атому, образуя электронное облако. Рассмотрим S- состояние. Это состояние является основным состоянием атома водорода. В нём / и m = О, и атом обладает минимальной энергией. Чтобы перевести атом из основного состояния в возбуждённое, ему необходимо сообщить энергию. Это может быть осуществлено либо за счёт теплового соударения атомов, либо за счёт столкновения атома с быстрым электроном. Либо за счёт поглощения атомом фотона.

Фотон при поглощении его атома передаёт ему всю свою энергию. Атом не может поглотить только часть фотона, т.к. фотон является неделимым. Поэтому может поглощать только те фотоны, энергия которых соответствует разности энергией двух его уровней. Это значит, что спектр поглощения атома водорода должен состоять из линий, соответствующих переходом.

Этот результат полностью согласуется с опытом. Вероятность нахождения электрона в шаровом слое для его различных энергетических состояний показана на графике. Здесь по оси ординат отложена плотность этой вероятности 4я7•^:!T², а по оси абсцисс радиус слоя. Как видно из графиков в состоянии IS имеется один максимум электронной плотности. У атома водорода он находится на расстоянии 0,53 А от ядра В состоянии 2 S-имеется два максимума электронной плотности из-за которых наиболее помещаемым является дальний максимум. В состоянии 3 S-имеется три максимума электронной плотности.

В Р-состояниях как показывает решение уравнения Шредингера, распределение

плотности электронного облака имеет вид:

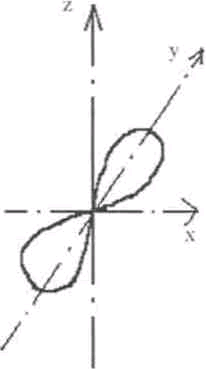
1=0 т=0

1=1 т=1

1=1 т= - 1

Значения Р могут быть любыми. Различие в главном квантовом числе сказывается на

изменении размеров картины: чем больше //, тем больше растянется картина.

В состояниях вероятность 4тп" Т' имеет максимум на таком расстоянии от ядра,.

которое совпадает с радиусом орбиты электрона в атоме.

В соответствии с основным положением квантовой теории энергия атома квантуется, т.

е. Может принимать ряд дискретных значений. Так как эта энергия зависит от

проекции магнитного момента на направление поля, то эта проекция квантуется по

следующему правилу: величина проекции сопоставляется с квантовым числом /»,

которое может принимать только целочисленные положительные и отрицательные

значения от -/ до +/, включая ноль.

Это значит, что:

т=+/, +(/-1). О -(/-1), -7.

Следовательно «т» может иметь всего 2/^ 1 значении.

При тщательном исследовании спектров оказалось, что спектральные линии имеют

тонкую структуру, наблюдаемую и в отсутствие внешних полей. Так, например, все

линии спектра водорода оказались состоящими из двух отдельных, близко

расположенных линий.

Для объяснения этого явления Юленбеком и Гаудсмитом была высказана гипотеза о

наличии у электрона собственного момента количества движения или «спина».

Подобно орбитальному моменту импульса спин электрона и его проекция на ось,

совпадающую с направлением внешнего магнитного поля, должны быть квантованы. В

квантовой механике доказывается, что спин электрона должен быть квантован по