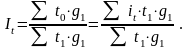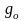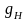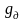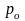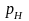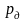- •Виды дисперсий, методика их расчета и условия применения в экономико-статистическом анализе.
- •3 Дисперсии количественного признака:
- •Предмет статистической науки. Основные статистические категории. Задачи статистики на современном этапе развития (в условиях рыночной экономики).
- •Статистическая сводка материалов наблюдения, ее значение в экономико-статистическом исследовании коммерческой деятельности.
- •Статистическая информация, ее значение и задачи в экономико-статистическом исследовании. Программа разработки первичных данных статистического наблюдения. Этапы сводки.
- •Показатели вариации
- •Основные показатели вариации
- •Методологические и организационные вопросы статистического наблюдения
- •Статистические индексы
- •Индексы с постоянными и переменными весами
- •Виды средних величин, условия их применения в экономическом анализе.
- •Средняя арифметическая
- •2. Сумма X(I)`*f(I)/ сумма f(I) – для интервального ряда распределения.
- •Средняя гармоническая
- •Средняя квадратическая
- •Средняя хронометрическая
- •Сезонные колебания в торговле, статистические методы выявления и математической оценки сезонной волны.
- •12. Абсолютные и относительные величины. Абсолютные статистические величины
- •Относительные статистические величины
- •Виды относительных величин
- •13. Статистические таблицы, их виды и значение в изложении результата статистической сводки. Основные правила построения статистических таблиц.
Индексы с постоянными и переменными весами
Если расчет агрегатных индексов физического объема продукции и товарооборота производится по неизменным ценам базисного периода, это позволяет, используя индексный ряд за несколько периодов, получить динамику стоимости продукции и динамику товарооборота в неизменных (сопоставимых) ценах, т.е. в ценах какого-то одного прошлого периода. Такие индексные ряды называются индексами с постоянными весами.
Для индексов с постоянными весами действует правило: произведение цепных индексов равно базисному индексу.
Пример 5. Имеются следующие данные об объеме производства и стоимости продукции:
Продукция |
Произведено продукции за I кв. |
Цена 2001г |
Стоимость продукции в неизменных ценах 2001 года, тыс.руб. |
||||||
2001 |
2002 |
2003 |
2001 |
2002 |
2003 |
||||
Продукция А, тыс.т. Продукция Б, млн.шт. |
60
5,5 |
64
6,2 |
69
7,0 |
5000
2000 |
300
11000 |
320
12400 |
345
14000 |
||
Итого |
|
|
|
|
11300 |
12720 |
14345 |
||
Требуется рассчитать индексы себестоимости с постоянными весами.
Базисные индексы:
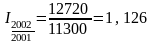
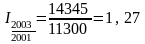
Цепные индексы:
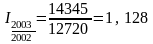
Взаимосвязь базисных и цепных индексов:

1,126 ·1,128 = 1,27.
Несколько иное положение с индексами цен, себестоимости и производительности труда. Если в качестве весов принимается количество продукции отчетного периода (q1), эти индексы образуют индексные ряды с переменными весами, поскольку в каждом отдельном индексе отчетный период изменяется.
Пример 6. Имеется следующая информация о продаже и ценах овощной продукции:
Товар |
Среднедневная продажа, кГ |
Цена за 1 кГ., руб. |
||||
октябрь |
ноябрь |
декабрь |
октябрь |
ноябрь |
декабрь |
|
|
|
|
|
|
|
|
Овощи Фрукты |
2400 1800 |
2000 1200 |
1800 800 |
1,2 1,0 |
1,0 1,8 |
2,2 2,5 |
Требуется рассчитать индексы цен с переменными весами.
Для изучения изменения цен по месяцам IV квартала определяются цепные и базисные общие индексы цен.
1. Среднее изменение цен в ноябре по сравнению с октябрем:
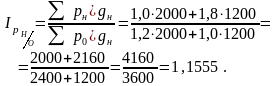
2. Среднее изменение цен в декабре по сравнению с ноябрем:
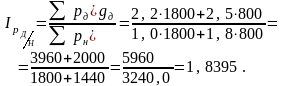
3. Среднее изменение цен в декабре по сравнению с октябрем:
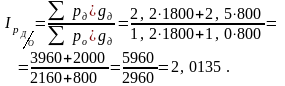
Индексы, построенные способом осреднения индивидуальных индексов, называются средними индексами.
Средний из индивидуальных индексов должен быть тождествен агрегатному индексу.
При исчислении средних индексов могут быть использованы только две формы средних:
а) средняя арифметическая;
б) средняя гармоническая.
Как правило, средний арифметический индекс применяется при индексировании первичных признаков, средний гармонический индекс – при индексировании вторичных признаков.
В средних арифметических индексах обычно берут веса базисного периода, в средних гармонических индексах – веса берут отчетного периода.
Всякий агрегатный индекс может быть преобразован в средний арифметический из индивидуальных индексов. Для этого индексируемая величина отчетного периода, стоящая в числителе агрегатного индекса, заменяется произведением индивидуального индекса на индексируемую величину базисного периода.
1). Индивидуальный индекс цен равен:
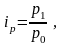 откуда
откуда
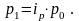
Тогда:
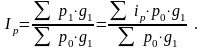
2).Аналогично строится средний арифметический индекс себестоимости:
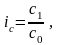 откуда
откуда
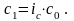
Следовательно:
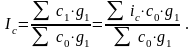
3). Таким же образом строится индекс физического объема продукции:
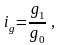 откуда
откуда
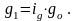
Следовательно:
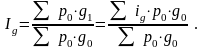
4). Средний арифметический индекс производительности труда образуется следующим образом:
при
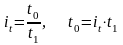 - это исключение.
- это исключение.
Тогда: